A Survey of Geometric Optimization for Deep Learning: From Euclidean Space to Riemannian Manifold
Y Fei, X Wei, Y Liu, Z Li, M Chen
[East China Normal University]
深度学习几何优化综述: 从欧几里德空间到黎曼流形
要点:
-
黎曼流形上的几何优化,可以解决深度学习中众所周知的问题,如梯度消失或梯度爆炸; -
调研了将几何优化应用于深度学习的最新进展,包括基本过程、各种几何优化器和黎曼流形的概念; -
调研了不同深度学习网络在各种AI任务中的应用,讨论了在流形上实现优化的典型开放工具箱; -
几何优化可以掌握搜索空间的几何信息,加快优化过程,缓解梯度爆炸和梯度消失问题,但在用于未开发的深度学习方法和流形结构时仍有挑战。
一句话总结:
黎曼流形上的几何优化可以缓解深度学习中的挑战,但挑战依然存在,特别是对于未开发的深度学习方法和流形结构。
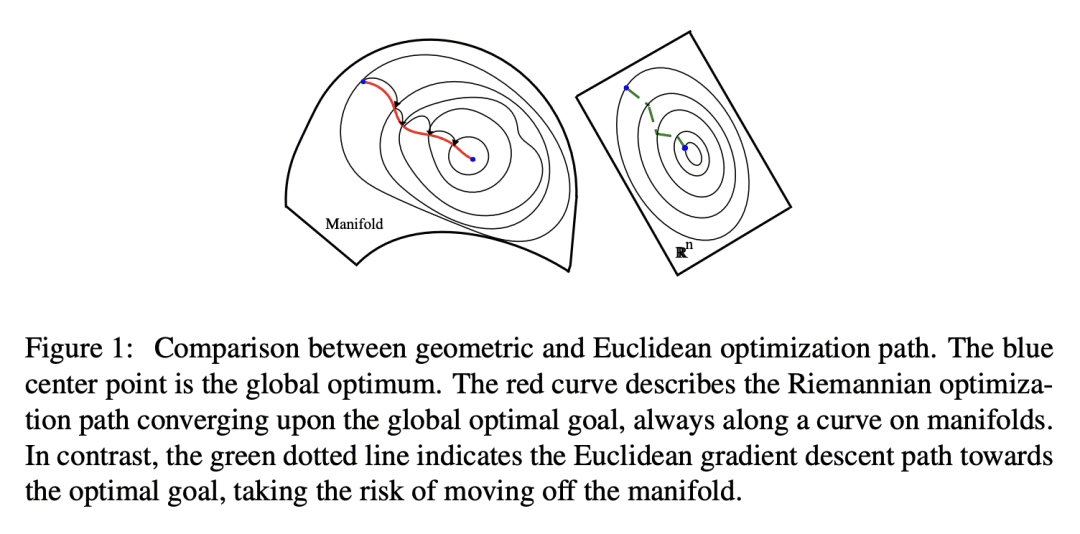
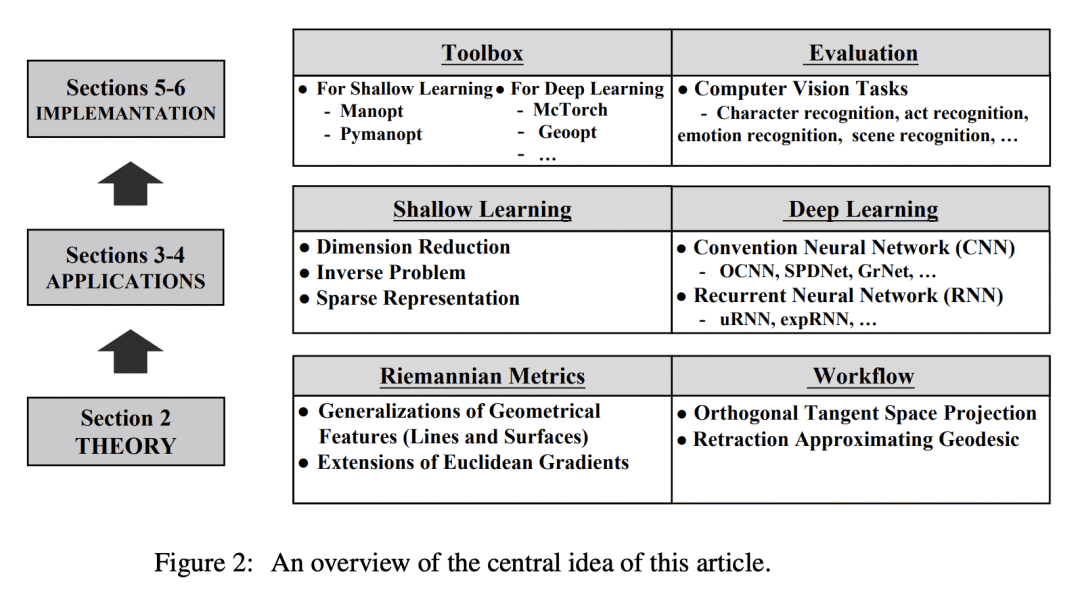
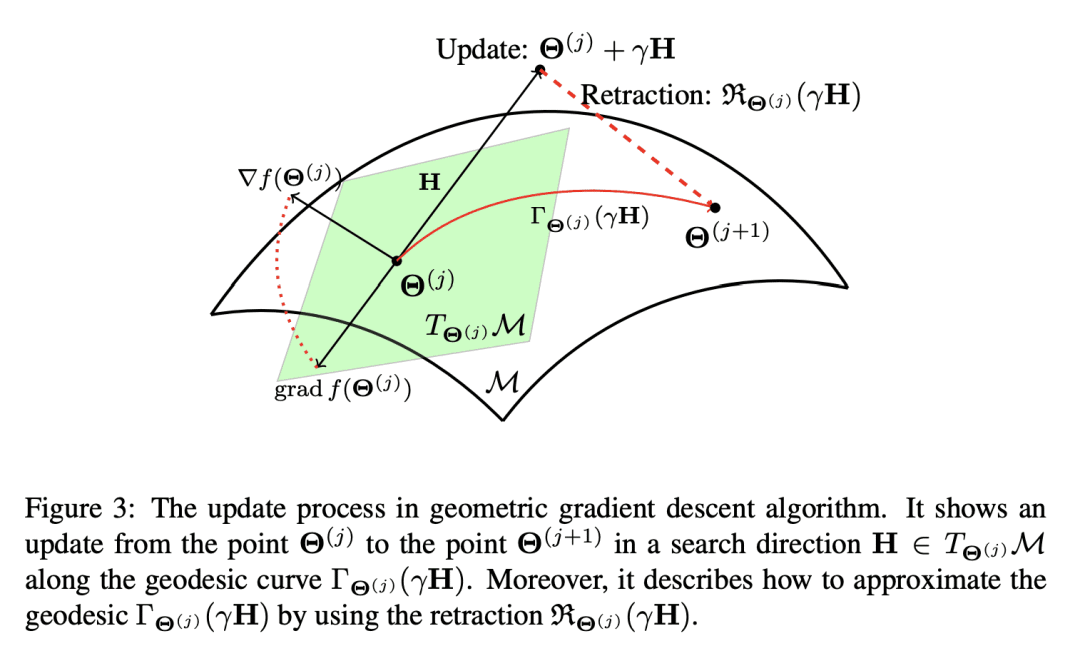
Although Deep Learning (DL) has achieved success in complex Artificial Intelligence (AI) tasks, it suffers from various notorious problems (e.g., feature redundancy, and vanishing or exploding gradients), since updating parameters in Euclidean space cannot fully exploit the geometric structure of the solution space. As a promising alternative solution, Riemannian-based DL uses geometric optimization to update parameters on Riemannian manifolds and can leverage the underlying geometric information. Accordingly, this article presents a comprehensive survey of applying geometric optimization in DL. At first, this article introduces the basic procedure of the geometric optimization, including various geometric optimizers and some concepts of Riemannian manifold. Subsequently, this article investigates the application of geometric optimization in different DL networks in various AI tasks, e.g., convolution neural network, recurrent neural network, transfer learning, and optimal transport. Additionally, typical public toolboxes that implement optimization on manifold are also discussed. Finally, this article makes a performance comparison between different deep geometric optimization methods under image recognition scenarios.
论文链接:https://arxiv.org/abs/2302.08210
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢