之前已经介绍过了利用加密电路或者比特分解来实现安全多方比较。本次再介绍一种利用不经意传输来实现双方比较的方法。

不经意传输在之前的科普进行过介绍,该比较协议的主要思路为:将需要比较的两个比特串分为多个部分,每个部分再进行比较,最后利用树形结构进行组合。假设有比特串𝑥和比特串𝑦,将比特串𝑥划分为两个部分,分别为𝑥1,𝑥0,将比特串𝑦也划分为𝑦1和𝑦0。
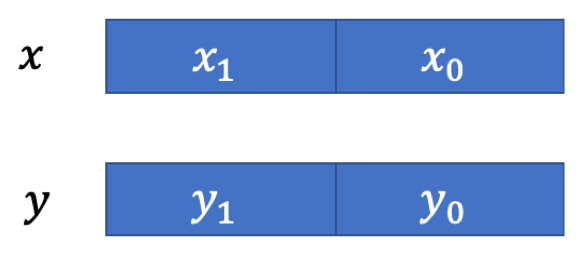
表达式1{𝑥<𝑦} 表示若𝑥<𝑦,则表达式1{𝑥<𝑦} 的值为1,否则为0。同理,表达式1{𝑥=𝑦 } 表示若𝑥=𝑦则表达式的值为1,反之为0。
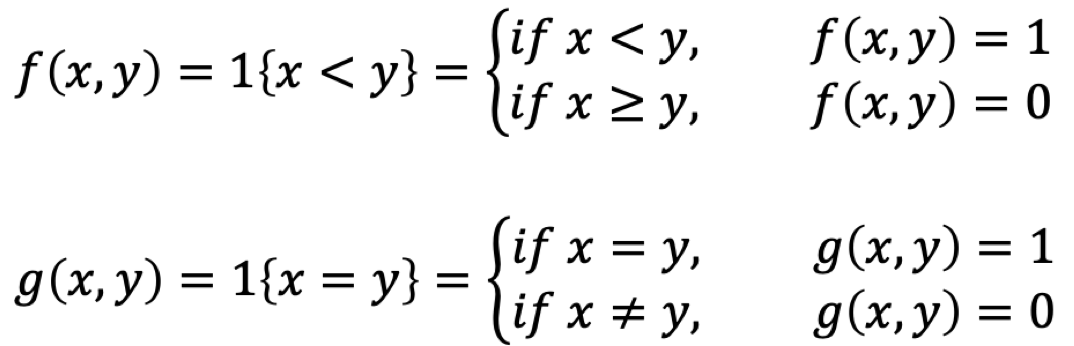
思考如下的比较:
![]()
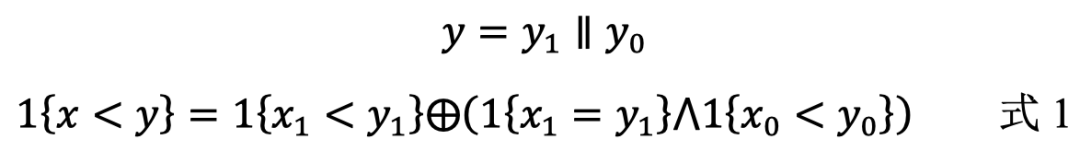
把比特串𝑥和比特串𝑦分为两部分后,先比较𝑥1和𝑦1的大小,由于𝑥1和𝑦1都是高位部分,因此若𝑥1<𝑦1则比特串𝑥<𝑦;反之若𝑥1>𝑦1则𝑥>𝑦,在这两种情况下无需在比较𝑥0,𝑦0的大小了。只有当𝑥1=𝑦1时,需要通过比较𝑥0,𝑦0的大小关系来确定𝑥, 𝑦的大小关系。
式1就是该比较协议的核心思想。该协议的详细流程为:
首先假设Alice掌握比特串𝑥,Bob掌握比特串𝑦,先考虑最简单的情况,𝑥和𝑦等长均为𝑙比特且![]() 为2的指数倍。
为2的指数倍。
1. Alice和Bob分别对𝑥和𝑦进行𝑞等分:
Alice:把𝑥进行𝑞等分,每份𝑚比特:
![]()
Bob:把𝑦进行𝑞等分,每份𝑚比特:
![]()
2. Alice产生两个随机数,将其分别记为![]() 。Alice利用
。Alice利用![]() 个比特,分别为
个比特,分别为![]() 来标识
来标识![]() 的大小关系;利用𝑀个比特,分别为
的大小关系;利用𝑀个比特,分别为![]() 来标识
来标识![]() 的相等关系:
的相等关系:
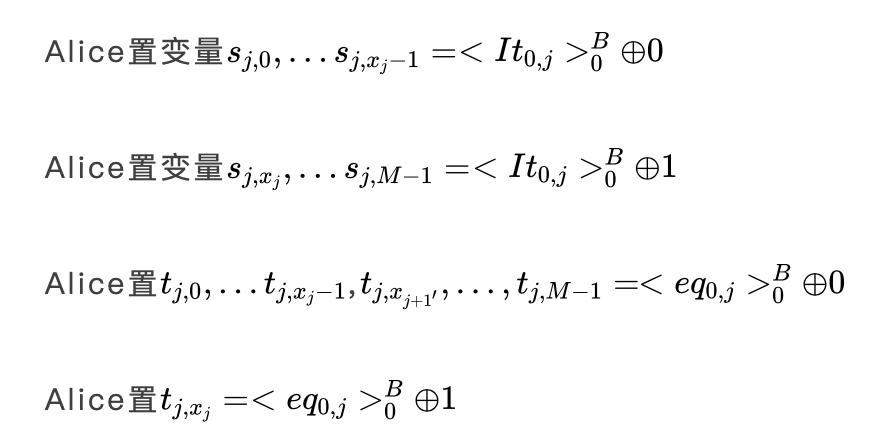
即对于![]() ,Alice将比特
,Alice将比特![]() 中下标为
中下标为![]() 的全都设置为随机数
的全都设置为随机数![]() ,将下标为
,将下标为![]() 的全都设置为
的全都设置为![]() 。例如段
。例如段![]() ,则𝑀=16。Alice将
,则𝑀=16。Alice将![]() 设置为
设置为![]() ,将
,将![]() 设置为
设置为![]() 。
。
即下标比![]() 的值小的为随机数
的值小的为随机数![]() 异或0,下标大于等于
异或0,下标大于等于![]() 的异或1。对于
的异或1。对于![]() ,则是只有当下标和
,则是只有当下标和![]() 相等时为随机数
相等时为随机数![]() 异或1,否则均为随机数
异或1,否则均为随机数![]() 异或0。
异或0。
若用黄色表示比特值为1,蓝色表示比特值为0,则Alice在完成上述步骤后,![]() 和
和![]() 如下所示:
如下所示:
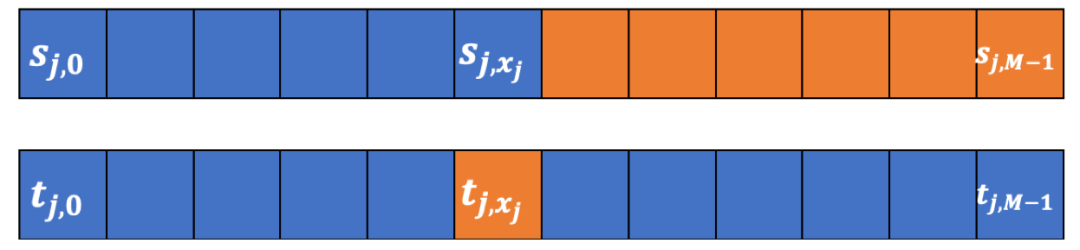
对于0≤𝑗≤𝑞−1,Alice对每个![]() 都进行上述的步骤,因此能得到
都进行上述的步骤,因此能得到![]() 共𝑞∙𝑀比特,得到
共𝑞∙𝑀比特,得到![]() 共𝑞∙𝑀比特。
共𝑞∙𝑀比特。
3. Alice和Bob间调用𝑞次𝑀选1的OT协议,Alice在 OT 协议中的输入为![]() ,Bob在OT中的输入为
,Bob在OT中的输入为![]() :
:

𝑞次𝑀选1的OT结束后,Bob会获得![]() 。
。
Alice和Bob再调用𝑞次𝑀选1的OT协议,Alice在OT协议中的输入为![]() ,Bob在OT中的输入为
,Bob在OT中的输入为![]() :
:

𝑞次𝑀选1的OT结束后,Bob会获得![]() 。将
。将![]() 记为
记为![]() ,将
,将![]() 记为
记为![]() 。
。
Alice的输入为![]() ,Bob的输入为
,Bob的输入为![]() ,那么当
,那么当![]() ≥
≥![]() 时,Bob通过OT获得的为
时,Bob通过OT获得的为![]() ,当
,当![]() <
<![]() 时,Bob通过OT获得的为
时,Bob通过OT获得的为![]() 。又由于Bob 通过OT获得的
。又由于Bob 通过OT获得的![]() 或者
或者![]() 异或上 Alice的随机数,
异或上 Alice的随机数,![]() 即为
即为![]() 的比较结果,因此可以将Bob获得的记为
的比较结果,因此可以将Bob获得的记为![]() ,看做是
,看做是![]() 的比较结果的一个子秘密。只有当Bob的子秘密
的比较结果的一个子秘密。只有当Bob的子秘密![]() 和 Alice的子秘密
和 Alice的子秘密![]() , 进行异或才能获得
, 进行异或才能获得![]() 的比较结果
的比较结果![]() 。
。
同理可将Alice的输入为![]() ,Bob的输入为
,Bob的输入为![]() ,OT后Bob获得的
,OT后Bob获得的![]() 记为
记为![]() ,作为Bob获得的
,作为Bob获得的![]() 的子秘密。
的子秘密。
4. Alice和Bob运行如下算法(Alice运行则𝑏=0,Bob 运行则𝑏=1):
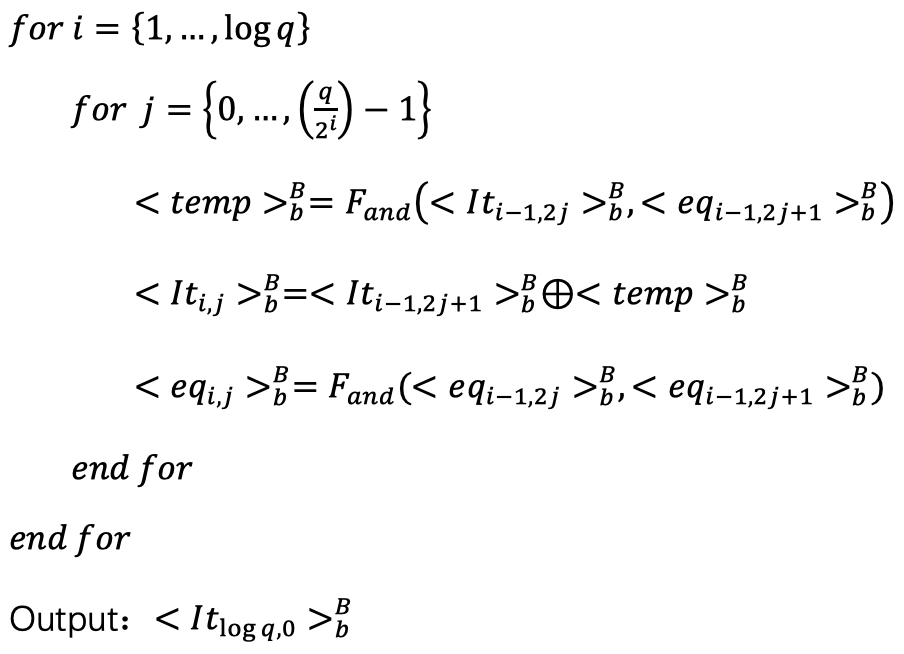
该算法的目的为将需要比较的比特串分成多个部分,每个部分进行比较, 再将比较结果进行组合。举个例子来解释这个算法,假设𝑞=16,则![]() ,要比较𝑥和𝑦先比较
,要比较𝑥和𝑦先比较![]() 和
和![]() 的大小,只有当
的大小,只有当![]() 和
和![]() 相等时才需要接着去比较
相等时才需要接着去比较![]() 和
和![]() 间的大小关系。而比较
间的大小关系。而比较![]() 和
和![]() 间的大小关系可以先比较
间的大小关系可以先比较![]() 和
和![]() 间的大小关系,若二者相等再比较
间的大小关系,若二者相等再比较![]() 和
和![]() ,以此类推,则形成了一个树形结构。
,以此类推,则形成了一个树形结构。
最后最先需要比较的为![]() 和
和![]() 间的大小关系。用:
间的大小关系。用:
![]()
表示该树形结构,(𝑖)表示位于第几层,如
![]()
树形结构如下图所示:
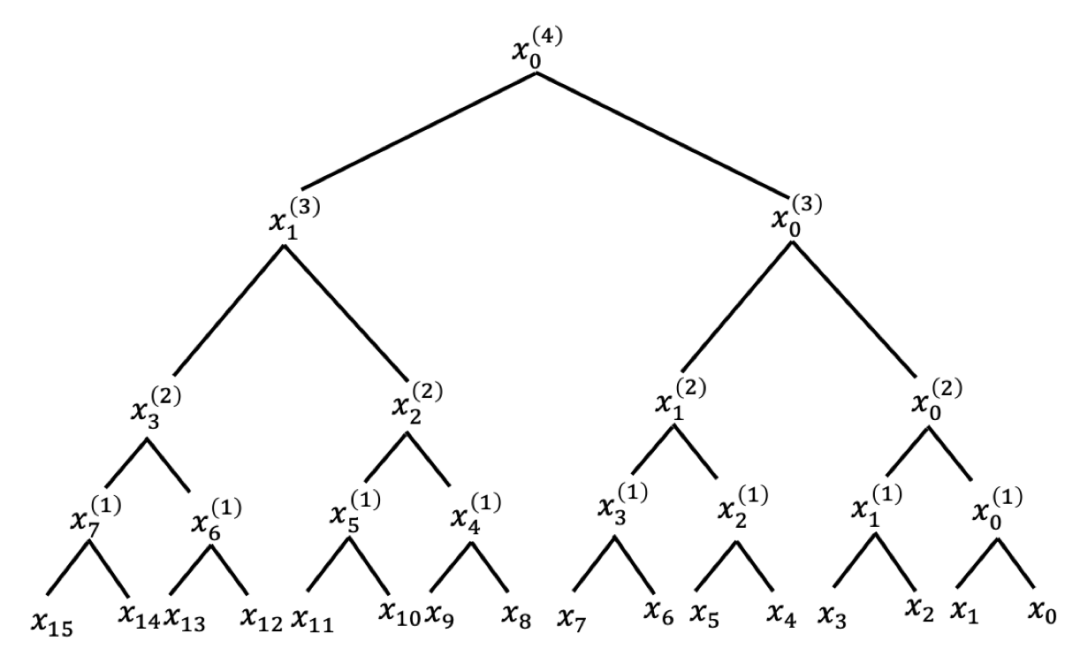
正确性证明:![]() 是多方𝑎𝑛𝑑函数,需要Alice和Bob共同完成𝑎𝑛𝑑操作。如𝐴𝑙𝑖𝑐𝑒掌握
是多方𝑎𝑛𝑑函数,需要Alice和Bob共同完成𝑎𝑛𝑑操作。如𝐴𝑙𝑖𝑐𝑒掌握![]() 和
和![]() ,Bob掌握
,Bob掌握![]() 和
和![]() ,二者都调用
,二者都调用![]() 后,
后,![]() 对Alice的输出为
对Alice的输出为![]() ,对Bob的输出为
,对Bob的输出为![]() ,具体实现可以使用之前介绍过的Beaver Triple完成,因此:
,具体实现可以使用之前介绍过的Beaver Triple完成,因此:
![]()
输出为:
![]()
则:
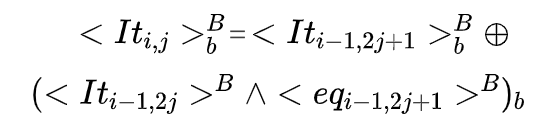
又由于:
![]()
因此对异或上可得:
![]()
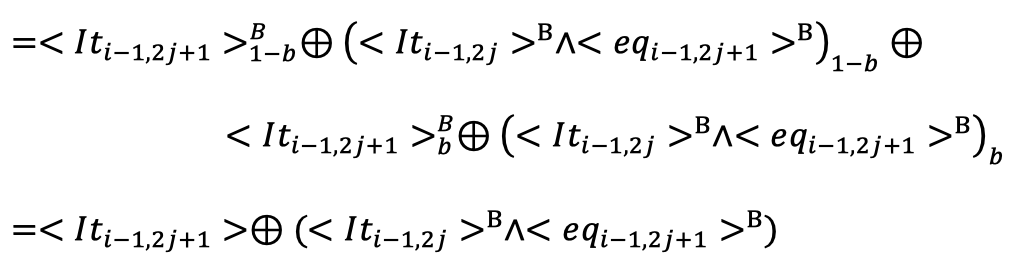
由此得证。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢