The Asymmetric Maximum Margin Bias of Quasi-Homogeneous Neural Networks
D Kunin, A Yamamura, C Ma, S Ganguli
[Stanford University]
准齐次神经网络非对称最大边际偏差
要点:
-
介绍了准齐次模型类,囊括几乎所有包含齐次激活、偏置参数、残差连接、池化层和归一化层的现代前馈神经网络架构。 -
梯度流隐性地偏向于准齐次模型中的一个参数子集,这与齐次模型中所有参数被平等对待的情况不同; -
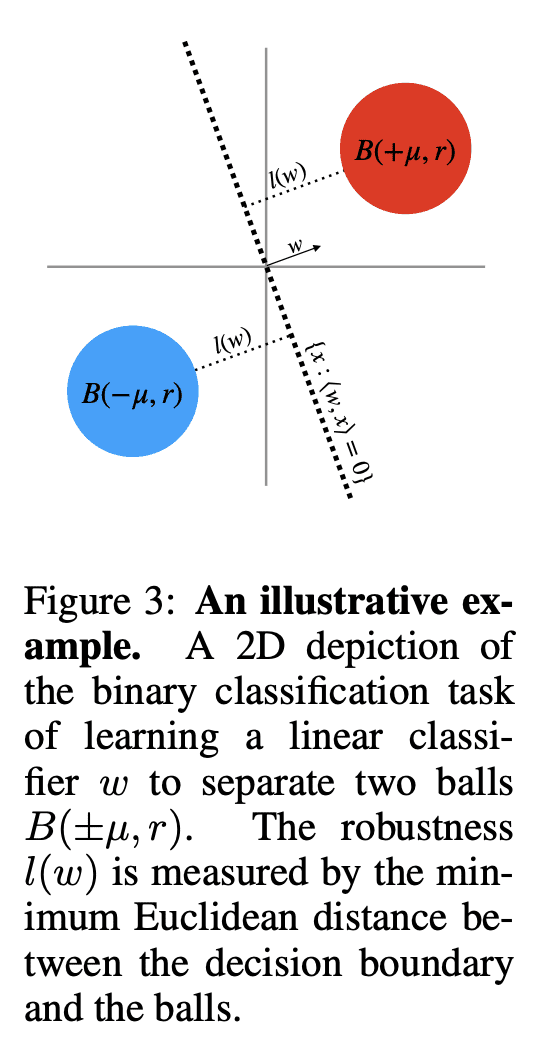
对非对称范数最小化的强烈偏好,会降低准齐次模型的鲁棒性,这一点通过简单的例子可得到证明; -
本文揭示了在具有规范化层的充分表现力的神经网络中,神经坍缩背后的普遍机制,这是由函数空间中的边际最大化和参数空间中 Λmax-seminorm 最小化之间的竞争导致的。
一句话总结:
探讨了准同态神经网络的最大边际偏差,揭示了神经坍缩这一经验现象背后的普遍机制。
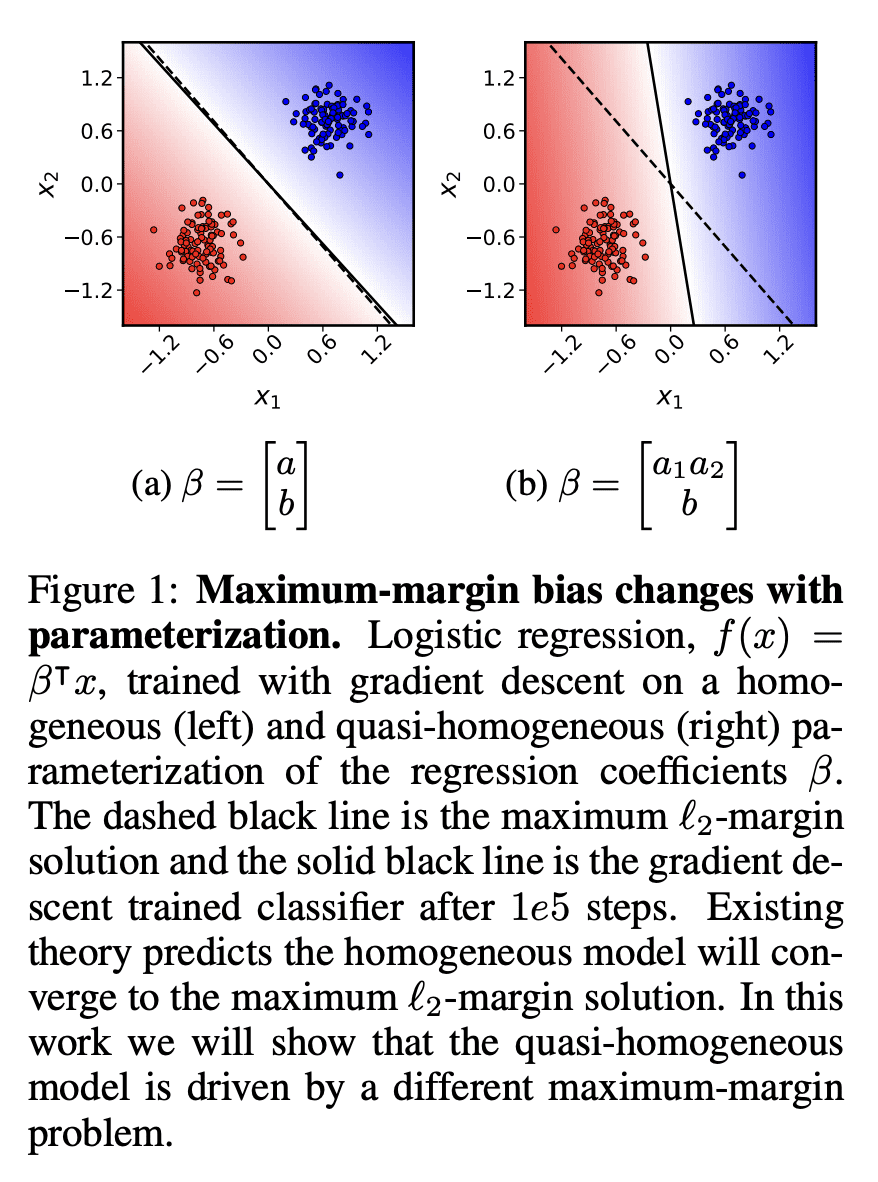
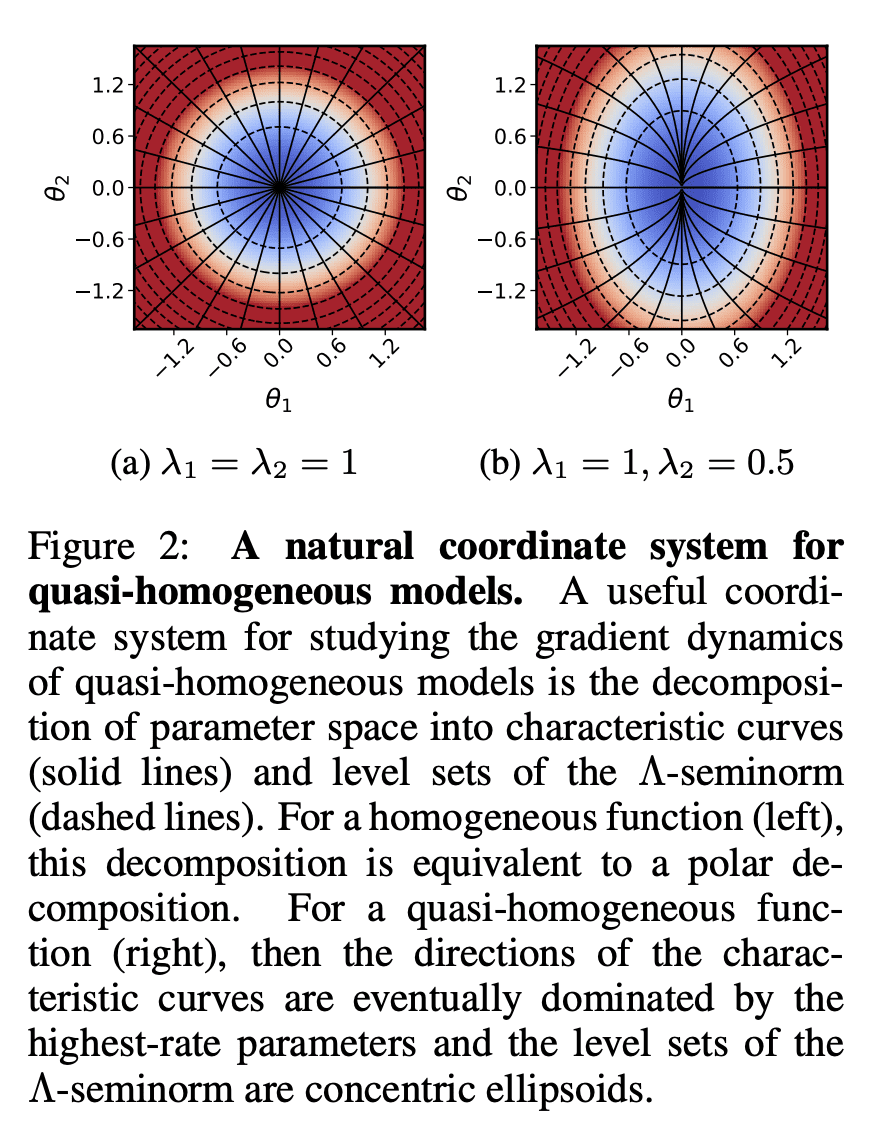
In this work, we explore the maximum-margin bias of quasi-homogeneous neural networks trained with gradient flow on an exponential loss and past a point of separability. We introduce the class of quasi-homogeneous models, which is expressive enough to describe nearly all neural networks with homogeneous activations, even those with biases, residual connections, and normalization layers, while structured enough to enable geometric analysis of its gradient dynamics. Using this analysis, we generalize the existing results of maximum-margin bias for homogeneous networks to this richer class of models. We find that gradient flow implicitly favors a subset of the parameters, unlike in the case of a homogeneous model where all parameters are treated equally. We demonstrate through simple examples how this strong favoritism toward minimizing an asymmetric norm can degrade the robustness of quasi-homogeneous models. On the other hand, we conjecture that this norm-minimization discards, when possible, unnecessary higher-order parameters, reducing the model to a sparser parameterization. Lastly, by applying our theorem to sufficiently expressive neural networks with normalization layers, we reveal a universal mechanism behind the empirical phenomenon of Neural Collapse.
论文链接:https://openreview.net/forum?id=IM4xp7kGI5V
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢