【隐私计算笔谈】MPC系列专题（十九）：三方复制秘密共享（五）

回顾一下，最近几次的科普我们介绍了三方复制秘密共享的秘密分享方式，其主要应用为作为隐私保护机器学习的隐私保护框架，将数据作为秘密，按机器学习对数据的操作进行安全多方计算。

机器学习需要对数据进行定点数的加法、乘法、矩阵运算等，需要三方复制秘密共享也有对应的这些操作。因此之后我们介绍了在和下三方复制秘密共享的乘法。在进行定点数运算时会带来定点数精度扩大问题，于是我们接着介绍了两个定点数截断算法Truncate I和Truncate II。秘密在三方复制秘密共享中有和两种表示方式，需要有互相转换的方式，我们接着介绍了将在下的子秘密转换为在下的子秘密的 Bit Decomposition算法。

有两种子秘密的表示形式，那么当需要两个不同表示形式的秘密进行计算，如需要子秘密和子秘密进行计算时又该怎么办呢？将转换为，或者将转换为进行计算，是一种办法。本次科普将介绍更高效的跨秘密表示形式的计算方法。在介绍实现夸秘密表示形式的计算方法之前，先介绍一种半诚实的三方OT和计算的方法。

三方OT

与双方 OT 相比，这个三方 OT 协议较为简单，是双方 OT 的一个变形，实际依旧只有两方进行OT，而让第三方作为 OT 协议的帮助者。假设参与者为Alice、Bob、Candy，Alice是秘密的发送方，Bob是秘密的接收方，而Candy则是帮助者，则整个三方 OT 协议可以被表示成,符号「⊥」表示空，即未接收到信息。

OT 协议的具体流程为：首先Alice和Candy共同产生两个𝑘比特的随机数，Alice和Candy都知道的具体值，接着Alice计算，并且将发送给Bob。Bob将自己的选择比特𝑐发送给Candy，Candy根据选择比特的值发送给Bob，Bob利用即可成功解密出。

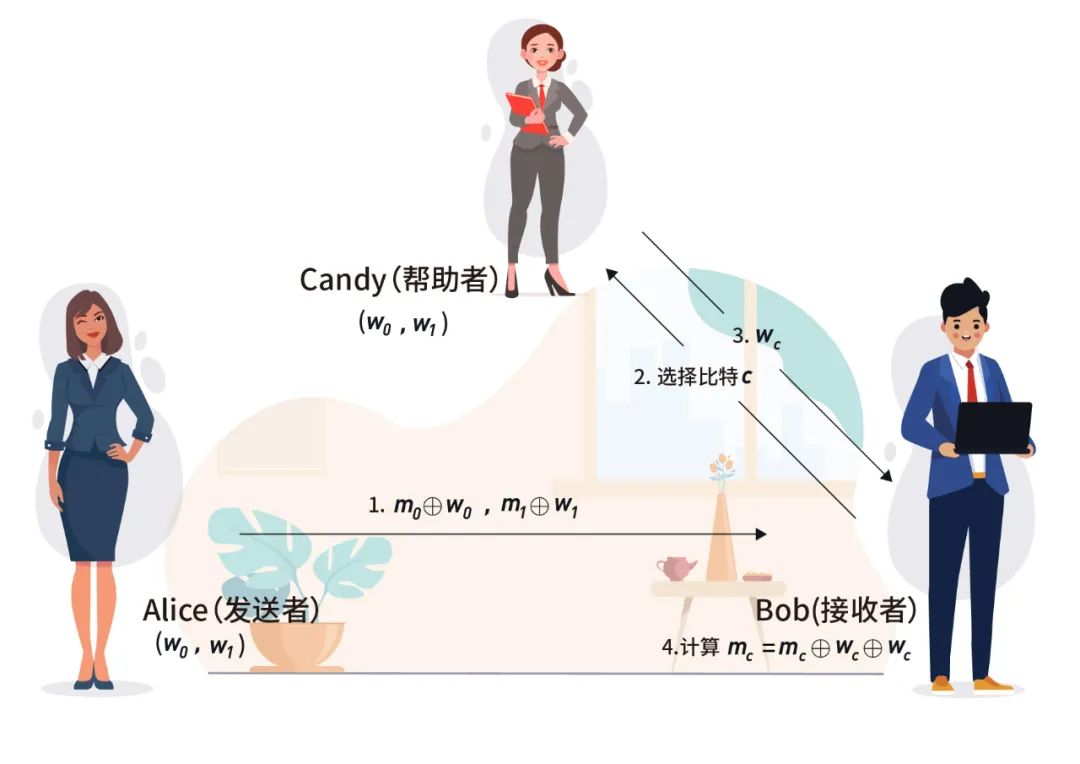
图：三方OT

完整执行完成后，Bob只获得了，Candy只知道而不知道，Alice只知道,而不知道Bob的选择，三者都只掌握了部分信息。

跨表示形式的子秘密计算

接着介绍计算的方式：最简单的例子是𝑎为上的明文，而𝑏为单比特。秘密𝑏以的形式被三方分享，Alice掌握，Bob掌握，Candy 掌握。首先Alice（发送者）在环上产生一个随机数 𝑟，接着产生两个消息和。Bob（接收者）掌握有，而Candy（帮助者）也掌握有，因此三者可以进行上述的三方OT。Alice作为 OT 的发送方，在这次 OT 中的输入为；Bob作为接收方，在这次OT的输入为；Candy则作为帮助者。注意都是单比特值，因此Bob通过OT可以获得。注意我们目标是让参与的三方获得。

接着，Alice、Bob和Candy可以利用之前预先产生的来计算。注意Bob已经获得了𝑏𝑎−𝑟，也掌握了，因此Bob可以本地计算，同样 Alice 也可本地直接计算，Candy本身就掌握有。

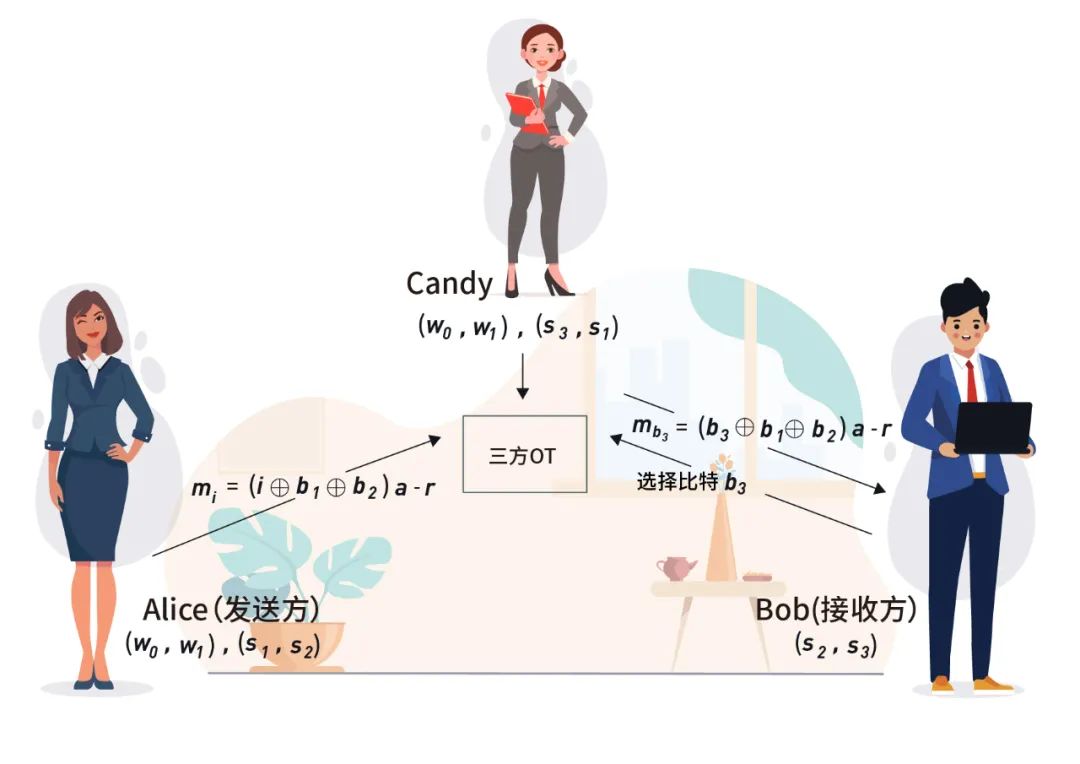
图：三方OT计算

回忆一下三方复制秘密共享的规则，要求Alice掌握,Bob掌握，Candy掌握。因此为了符合复制秘密共享的规则，Bob计算之后，需要再将发送给Alice，同样Alice在计算完后需要将它发送给Candy。或者也可以再进行一次三方OT，这次由 Bob来扮演发送方，Bob在OT协议的输入为，接收方由Alice扮演，Alice输入选择比特来获得消息。这样就成功的完成了的计算。