在Transformer架构中,正弦和余弦函数常常被用作序列的位置编码(Positional Encoding,PE)。然而,对于图,正弦函数没有明确的定义,因为图中没有沿着轴的位置概念。因此,作者选择使用图拉普拉斯矩阵(Graph Laplacian,L)的特征向量φ作为图的位置编码。这也是本文的核心。拉普拉斯算子对应于梯度的散度,其特征函数是正弦/余弦函数,其中平方频率对应于特征值。因此,在图领域中,图拉普拉斯矩阵的特征向量自然地成为了正弦函数的平替。

这篇论文提出了一种新的图神经网络模型,名为谱注意力网络(Spectral Attention Networks,SAN)。SAN模型是基于Transformer的,它通过学习位置编码(Positional Encoding,PE)来感知给定图网络的Laplace谱。这种方法允许模型使用图的整个Laplace谱,学习频率如何相互作用,并决定哪些频率对于给定任务最重要。
小编(GNN4AI):Laplace谱是图的一种重要特性,它可以揭示图的许多重要信息,如图的连通性、聚类系数等。在图神经网络中,Laplace谱可以被用来生成节点的嵌入,这些嵌入可以捕捉到节点的上下文信息,从而提高模型的性能。在这篇论文中,作者提出了一种新的方法,允许模型使用图的整个Laplace谱。这意味着模型可以获取到更多的图结构信息,从而生成更准确的节点嵌入。此外,这种方法还允许模型学习频率之间的相互作用,这可以帮助模型理解图的复杂结构。最重要的是,这种方法还允许模型决定哪些频率对于给定任务最重要。这是一个重要的特性,因为不同的任务可能需要关注图的不同特性。例如,一些任务可能需要关注图的全局结构,而其他任务可能需要关注图的局部结构。通过学习哪些频率最重要,模型可以自动地适应不同的任务,从而提高其性能。使用图拉普拉斯矩阵的特征向量作为位置编码,是因为它们可以更好地捕捉图的全局结构信息,而不仅仅是序列的位置信息。

生成LPE[learned positional encoding (LPE)]矩阵:首先,模型会计算图的Laplace矩阵,然后求解这个矩阵的特征值和特征向量。接着,模型会将这些特征值和特征向量转换为一个连续的位置编码(PE),这个PE可以表示节点在图中的位置。具体的转换方法可以是通过一个全连接层或者一个多层感知机。LPE Transformer:
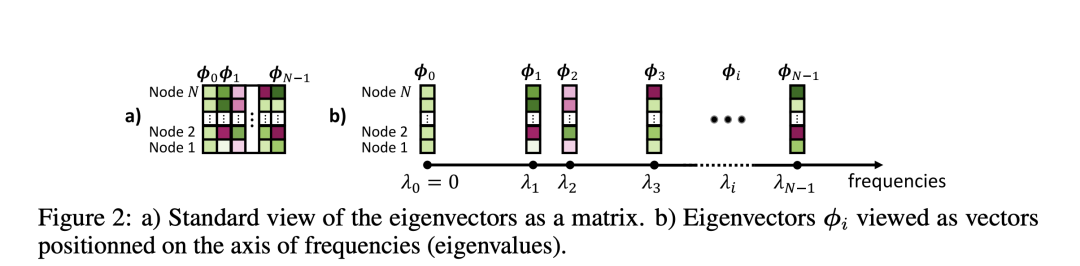
连接LPE矩阵和节点嵌入:在这一步中,模型将LPE矩阵与节点嵌入进行连接。节点嵌入是节点的另一种表示,它通常是通过图神经网络从节点的特征和图的结构中学习得到的。通过将LPE矩阵和节点嵌入进行连接,模型可以同时考虑节点的特征、节点在图中的位置以及图的全局结构。
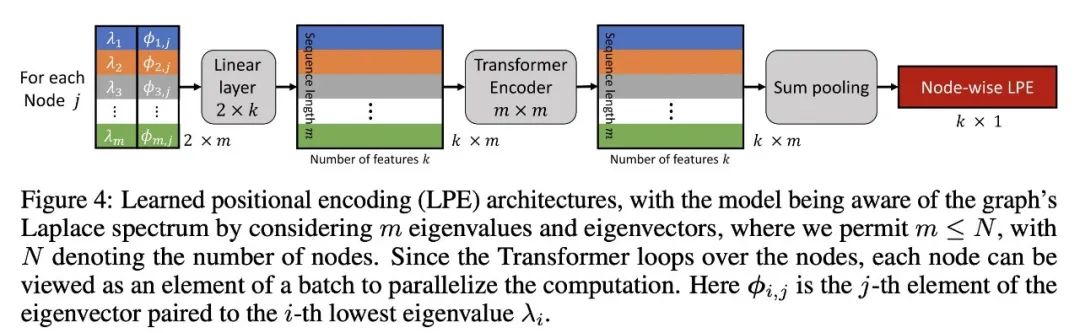
传递给图Transformer:在这一步中,模型将连接后的节点嵌入传递给另一个Transformer,这个Transformer被称为图Transformer。图Transformer的任务是处理图的全局信息,生成最终的节点嵌入。这些节点嵌入可以被用来进行各种图相关的任务,如节点分类、图分类等。
通过这个两步学习过程,SAN模型可以有效地利用图的Laplace谱,生成准确的节点嵌入,从而提高模型的性能。
在ZINC, PATTERN, CLUSTER, MolHIV和MolPCBA等数据集上的实验结果表明,SAN模型的性能与最先进的方法相当或更好。特别是在PATTERN和CLUSTER这两个数据集上,SAN模型的性能显著优于其他基于注意力的模型。 通过对比实验,作者发现全连接的注意力机制对于处理大型图(如PATTERN和CLUSTER数据集)更有优势,而对于处理分子图(如ZINC和MOLHIV数据集),局部结构(如环和特定的键)的理解更重要,因此全连接的注意力机制的优势就不那么明显了。 作者还发现,提出的节点LPE对于分子任务(如ZINC和MOLHIV)的性能提升有显著贡献,这可能是因为它能够检测到子结构(如环和特定的键)。
总的来说,这篇论文提出了一种新的图神经网络模型,光谱注意力网络(Spectral Attention Networks,SAN),它是基于Transformer的,并且能够通过学习位置编码来感知给定图的Laplace谱。实验结果表明,SAN模型在多个基准测试中的性能与最先进的方法相当或更好,特别是在处理大型图的任务上,其性能显著优于其他基于注意力的模型。然而,由于Transformer的计算复杂度较高,SAN模型在处理大型图时也面临一些挑战,如何降低计算复杂度,提高模型的效率将是未来的研究方向。
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢