Nat. Commun.速递：利用最优输运和流形学习发现守恒律

关键词：守恒量，流形学习，非线性动力学，扩散映射

论文标题：Discovering conservation laws using optimal transport and manifold learning
论文来源：Nature Communications
斑图链接：https://pattern.swarma.org/paper/0f63d2b4-3577-11ee-b6ce-0242ac17000d
原文链接：https://www.nature.com/articles/s41467-023-40325-7

守恒律是理解、描述和模拟非线性动力系统的重要理论和实践工具。然而，对于许多复杂系统来说，相应的守恒量难以确定，因此很难对其进行动态分析并建立稳定的预测模型。

目前发现守恒律的方法通常依赖于详细的动力学信息，或者依赖于黑盒参数深度学习方法。本文将这一任务重新表述为流形学习问题，并提出一种发现守恒量的非参数方法。

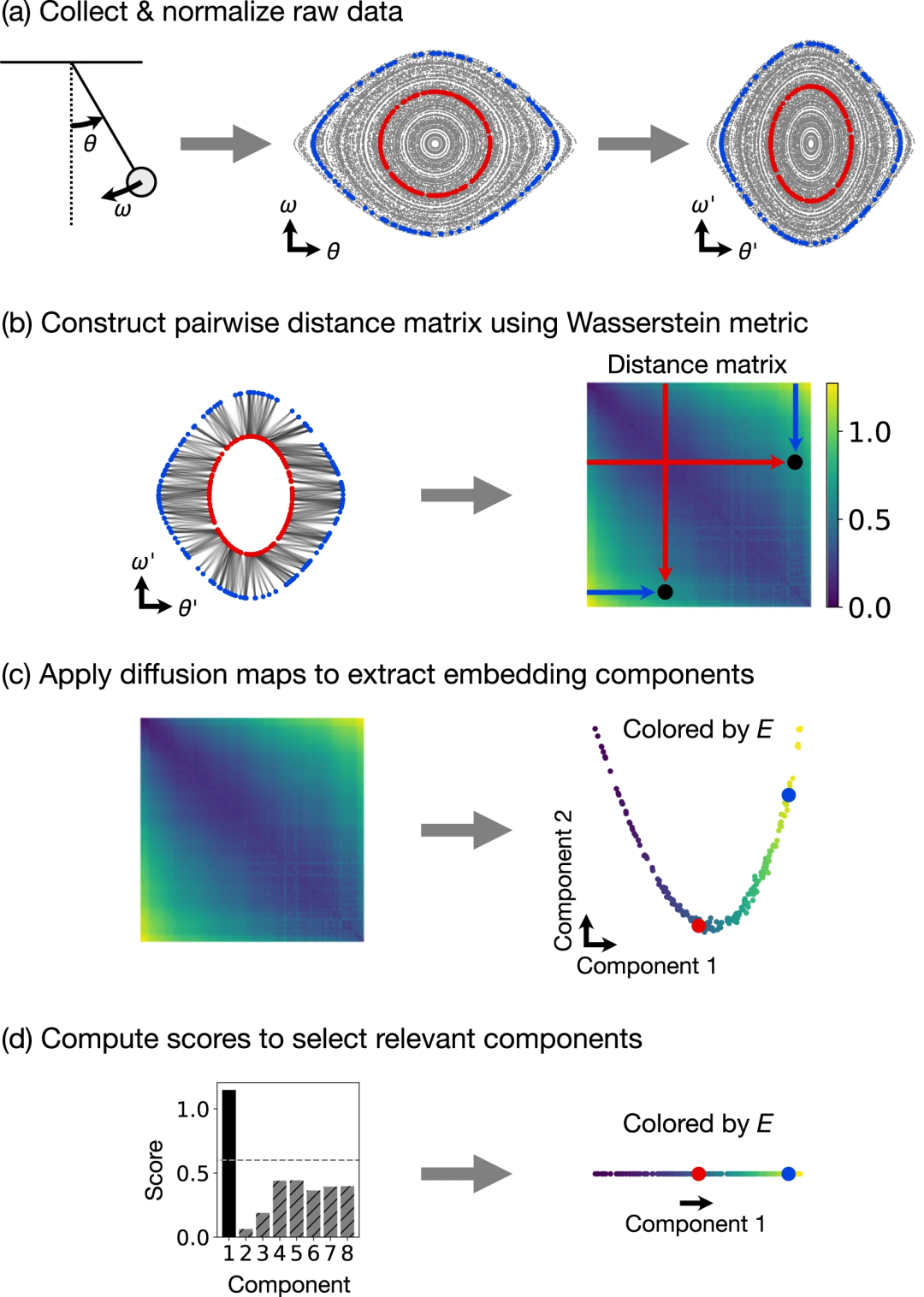
图1 以简摆例子说明守恒律的拟议非参数方法。a.收集动力系统的轨迹数据并进行归一化处理；b.使用最优输运中的瓦瑟斯坦度量计算每对轨迹之间的距离，并构建距离矩阵；c.利用扩散图从距离矩阵中提取形状空间流形 C 的嵌入，嵌入图由摆的守恒能量E着色；d.使用启发式评分来选择相关成分。

本文还在在各种物理系统上测试了这种新方法（单摆和双摆、平面引力动力学、浅水波的 KdV 方程，以及产生振荡图灵模式的非线性反应-扩散方程），证明该方法既能识别守恒量的数量，又能提取它们的值。

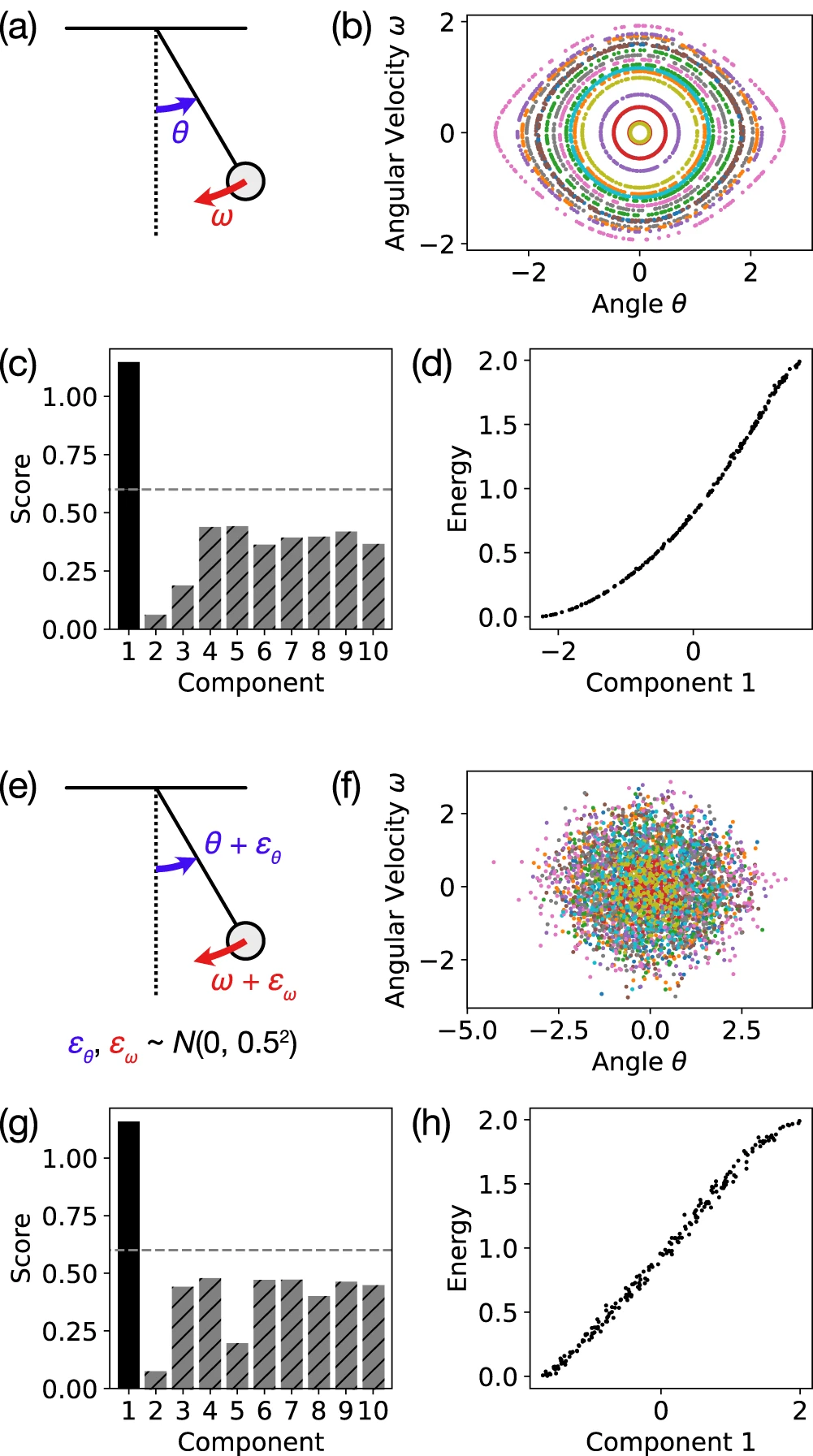
图2 识别单摆的守恒能量。a. 单摆有两个自由度：角度θ和角速度ω；b.根据样本轨迹在二维相空间 (θ, ω) 中绘制的样本点；c. 启发式评分正确识别出扩散图提取的第一个嵌入分量是唯一相关的分量，并且d.提取的第一个分量与能量单调相关；e, f. 加入σ= 0.5的高斯噪声，g. 启发式评分仍将第一个分量识别为相关分量，并且 h.该分量与能量非常吻合

经验证，这种方法既稳健又可解释，不需要明确的系统模型，也不需要精确的时间信息，同时也证明对测量轨迹中的噪声、以部分观测到的相空间为形式的缺失信息以及近似守恒律的鲁棒性，优于之前基于深度学习的直接拟合方法，同时速度快了一个数量级。

编译｜董佳欣

AI+Science 读书会