太长不看版

AFFNet 设计了一种自适应频段过滤算子：Adaptive Frequency Filtering token mixer。视觉 Transformer，Large-Kernel CNN 和 MLP 在很多视觉任务上面都取得了成功，归功于它们的 token mixer 在全局范围内的信息融合。但是这些 token mixer 的成本较高，在移动设备上的高效部署存在一定的挑战。自适应频段过滤算子就是为了解决这个问题，它通过傅里叶变换 (Fourier transform) 将特征变换到频域，并利用下面关系在数学上的等价：

• 在频域中 "通过逐位置的乘法操作过滤不同频段的特征"。
• 在空域中 "用一个动态卷积核执行特征混合操作，卷积核的大小为特征的大小"。

实验结果表明，与其他轻量级网络设计相比，AFFNet 在大多数视觉任务 (包括视觉识别和密集预测任务) 上实现了更好的精度和效率的权衡。

1 AFFNet：频域自适应频段过滤=空域全局动态大卷积核

论文名称：Adaptive Frequency Filters As Efficient Global Token Mixers (ICCV 2023)

论文地址：

https://arxiv.org/pdf/2307.14008.pdf

1.1 背景和动机

AFFNet 设计了一种自适应频段过滤算子：Adaptive Frequency Filtering token mixer。视觉 Transformer，Large-Kernel CNN 和 MLP 在很多视觉任务上面都取得了成功，归功于它们的 token mixer 在全局范围内的信息融合。但是这些 token mixer 的成本较高，在移动设备上的高效部署存在一定的挑战。

自适应频段过滤算子就是为了解决这个问题，它利用卷积定理 (convolution theorem[1][2][3])，即：在一个域中的卷积在数学上等于其对应的傅里叶域中的 Hadamard 积 (也称为 Elementwise 乘积)。它的特点力求和 Self-Attention 对齐，包括：

a. 全局信息建模 (Large Scope)

在频域中进行 Hadamard 积运算等价为在空域中进行大卷积核运算。

b. 输入自适应 (Instance-Adaptive)

Self-Attention 的另一个性质是输入自适应，即计算出的 Attention 权重与输入图片的内容有关。动态卷积满足这一性质，但是同样存在计算代价高昂的问题，尤其是大核卷积的情况。所以似乎直接加大卷积核很难直接满足这个需求。

1.2 Token Mixing 过程的一般表示

假设输入是 其中 是特征的高和宽, 是特征的通道数, 它可以被视为是一系列的 tokens, 其中每个 tokens 的维度是 。对于特征 , 经过 token mixing 之后得到 的这个过程可以统一描述为下式：

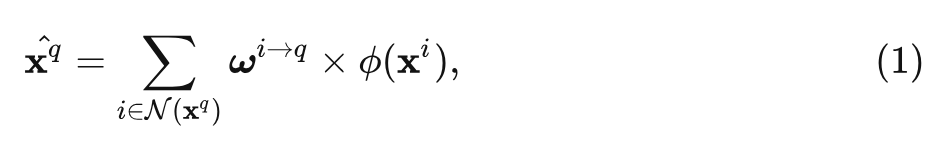
式中, 代表原始特征中的每个 token, 代表一个嵌入函数, 代表信息融合过程中的权重， 代表矩阵乘法或者 Hadamard 积。

对于 CNN 模型，如果想使用大卷积核，那么卷积的计算复杂度随总的 token 数呈 的关系，对于 Transformer 模型，Self-Attention 的计算复杂度随总的 token 数也呈 的关系。MLP-Mixer 模型如果实现全局感受野需要大量的权重参数。因此自适应频段过滤算子希望借助频域设计高效，全局，以及输入自适应的算子。

1.3 自适应频段过滤算子的原理

假设输入特征是 其中 是特征的高和宽, 是特征的通道数, 卷积过程可以写成:

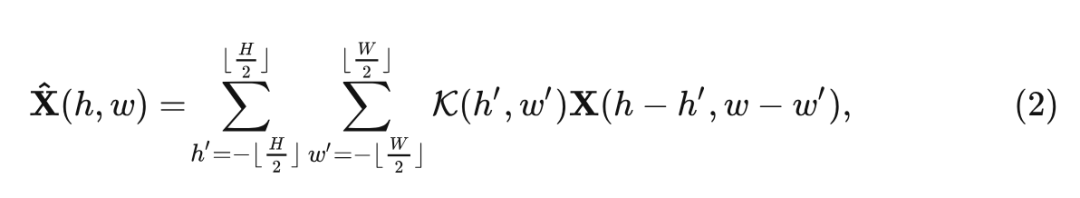
式中, 是输出特征, 是 Token Mixing 特征的权重。

为了设计全局, 以及输入自适应的算子, 应该随着输入特征 的变化而变化, 同时具有大感受野。

如下图1所示，自适应频段过滤算子的做法是：

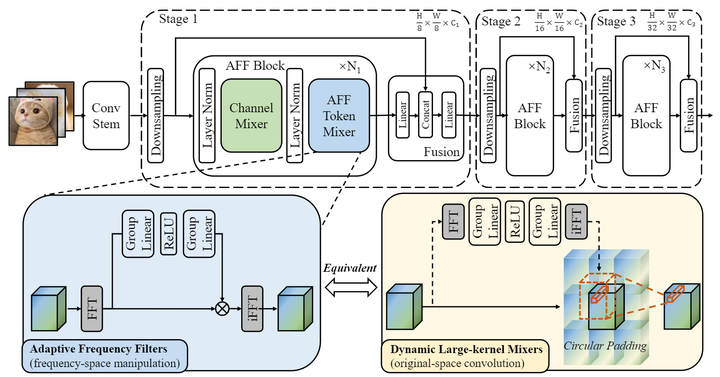
1) 首先把输入特征做快速傅里叶变换 (Fast Fourier Transform， FFT) 转换到频域 , 其中 为:

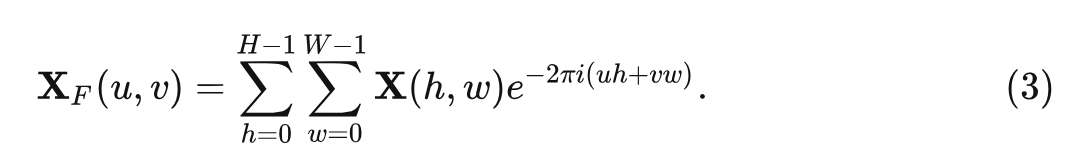
快速傅里叶变换的计算复杂度是 。

2) 通过可学习的频域滤波器 点乘输入的频域特征：

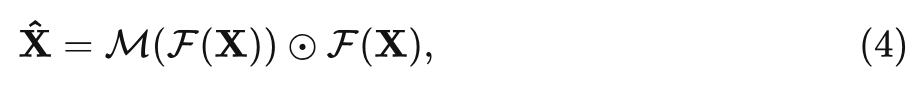
式中, 是可学习的频域滤波器, 和频域特征有相同的形状。为了使网络尽可能轻量化, 由 卷积层, 即线性层, ReLU 激活函数和一个线性层实现。

3) 通过快速傅里叶逆变换 (Inverse Fast Fourier Transform, IFFT) 转换回到空域：

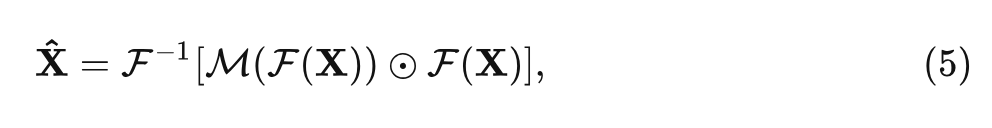
至此， 在数学上等价于采用大核动态卷积作为 Token Mixer 的权重得到的输出结果。

等价关系如下：

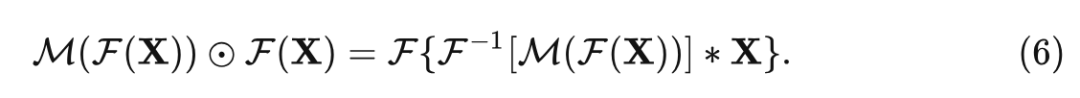
根据式5和6，有：

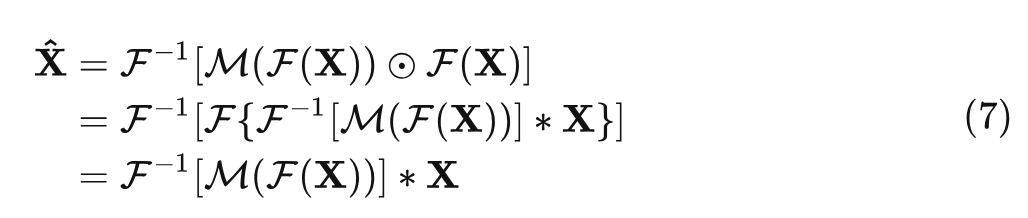
其中, 是与 形状相同的张量, 可以看作是大核动态卷积的卷积核 (满足性质 : 全局信息建模), 这个 Kernel 与输入内容有关 (满足性质 : 输入自适应)。因此, 在数学上等价于采用大核动态卷积作为 Token Mixer 的权重得到的输出结果。根据傅里叶变换的性质, 对 采用 circular padding。

总结一下, 自适应频段过滤算子使用极轻量级的网络搭了一个可学习的频域滤波器 , 然后计算 与频域特征之间的 Hadamard 积进行自适应频率滤波。最后再将特征通过傅里叶逆变换, 变换到空域。至此, 频域自适应频段过滤就相当于是空域全局动态大卷积核。

1.4 AFFNet 网络架构

整体的网络架构如图1上方所示，每一层包括一个 MBConv 模块和一个自适应频段过滤算子。遵循 Transformer 架构的一般设计范式使用 Layer Normalization 归一化。整体架构可以写成下式：

堆叠多个 AFF 块来构建轻量级骨干网络，即 AFFNet，AFFNet 使用惯例做法 Convolution Stem 来处理输入图片，每个 Stage 之间使用一个 Fusion 模块来融合特征。

1.5 实验结果

ImageNet-1K 图像识别实验结果

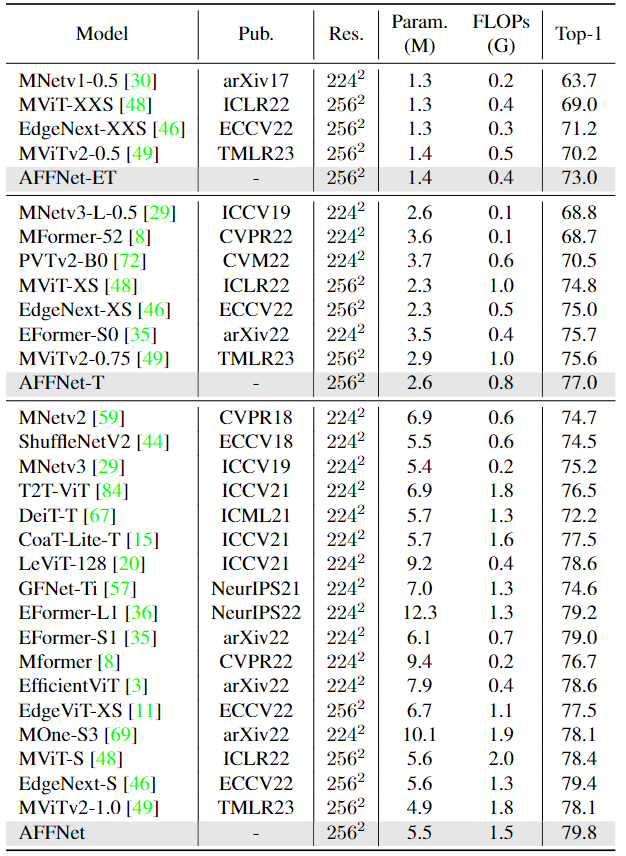
实验结果： 如图2所示，可以观察到，AFFNet 在 ImageNet-1K 的 Top1 精度度方面优于其他具有可比模型大小的轻量级网络。AFFNet 在 5.5M 参数和 1.5G FLOPs 的情况下达到了 79.8% 的 Top-1 准确率。极小模型 AFFNet-ET 以 1.4M 和 0.4G FLOPs 达到 73% 的 Top-1 准确率。AFFNet 在准确性和效率之间实现了很好的权衡。

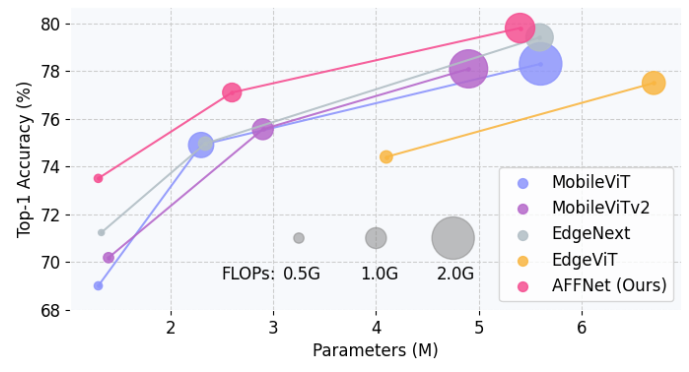
为了更直观地展示比较结果，作者在图3中说明了 AFFNet 和一些具有全局 Token Mixer 的高级轻量级模型相比之下的准确度和效率权衡。AFFNet 在不同的模型尺度上明显优于它们，而且模型越小的时候性能的优势越明显。AFFNet、AFFNet-T 和 AFFNet-ET 模型在单张 A100 上的吞吐量分别是 4202, 5304, 和 7470 images/s，比 MobileViT-S/XS/XXS 分别快了 13.5%、8.2% 和 14.9%。

COCO 目标检测实验结果

实验设置： 数据集使用 COCO，检测头使用 Single Shot Detection (SSD)，采用可分离卷积代替检测头中的标准卷积，Backbone 部分的权重初始化使用 ImageNet-1K 预训练权重，使用 AdamW 优化器在 MS-COCO 的训练集上微调整个模型 200 个 Epoch，图片的输入分辨率是 320×320。

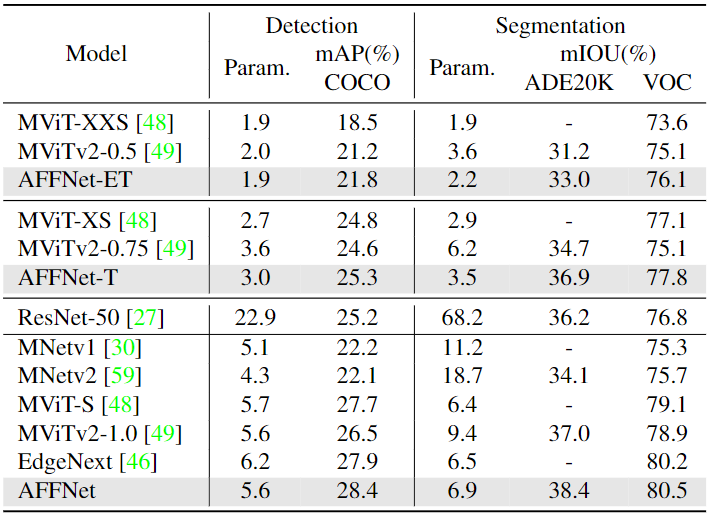
实验结果如图4所示。配备 AFFNet 的检测模型在不同模型尺度的 mAP 中始终优于其他基于轻量级 CNN 或基于视觉 Transformer 的检测器。具体而言，AFFNet 第二好的 EdgeNext 0.5%，同时节约了 0.6M 的参数量，并使用大约 1/4 的参数超过了 ResNet-50 主干的模型 3.2%。最小的模型 AFFNet-ET 性能优于第二好的模型 MobileViTv2-0.5 0.6%，同时参数量相当。这些结果表明，AFFNet 在以较低的成本捕获目标检测任务所需的空间位置信息方面的有效性。

ADE20k 语义分割实验结果

实验设置： 数据集使用 ADE20k 和 PASCAL VOC 2012，语义分割头使用 DeepLabv3。Backbone 部分的权重初始化使用 ImageNet-1K 预训练权重，在 ADE20k 和 PASCAL VOC 2012 的训练集上再训练整个模型120和50个 Epoch，图片的输入分辨率是 512×512。

实验结果如图5所示。AFFNet 在这两个数据集上的表现明显优于其他轻量级网络。AFFNet 比第二好的轻量级网络 MobileViTv2-1.0 在 ADE20k 的 mIOU 上面高出 1.4%，在 VOC 上的 mIOU优于第二好的轻量级模型EdgeNext 0.3%。

消融实验结果

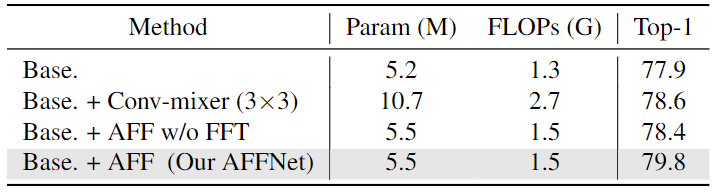
为了验证频域中混合信息的有效性，作者比较了在原始域和频域应用相同的自适应过滤操作，即进行了下面的实验：丢弃所有的傅里叶和傅里叶反变换，并保持其他与 AFFNet 相同，命名为 "Base.+AFF w/o FFT"。实验结果如下图5所示。在相同的模型复杂度下，AFFNet 明显高出 1.4% 的 Top-1 精度。在原始域中应用自适应滤波甚至比仅仅用 Conv 作为 Token Mixer 弱 (取得了 78.6% 的 Top-1 精度，命名为 "Base.+Conv-mixer (3×3)")，这表明只有自适应频率滤波器可以作为有效的全局 Token Mixer。AFFNet 实验结果命名为 "Base.+AFF (Our AFFNet)"。

参考

1. ^Continuous And Discrete Signal And System Analysis
2. ^Theory and application of digital signal processing
3. ^Discrete-Time Signal Processing