【ELAMN回归预测】基于鲸鱼算法优化ELMAN神经网络实现数据回归预测附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法  神经网络预测 雷达通信 无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机 电力系统

⛄ 内容介绍

针对房价受到多个相关因素的影响且EIman神经网络随机产生的权值及阈值导致预测结果精度较低等难题,提出了一种基于鲸鱼算法优化EIman神经网络的房价预测方法.首先,利用鲸鱼算法的优化特性进行EIman神经网络权值,阈值的优化,完成EIman的重构;然后,以波士顿房价为例并考虑房价的影响因素,构建训练集和测试集;最后,利用WOAEIman与EIman分别进行波士顿房价的预测,测试结果表明,WOA-EIman的预测精度高于EIman,其测试集均方差MSE低于EIman.

⛄ 部分代码

%_________________________________________________________________________%

%  Whale Optimization Algorithm (WOA) source codes demo 1.0               %

%                                                                         %

%                                                                         %

%_________________________________________________________________________%

% You can simply define your cost in a seperate file and load its handle to fobj 

% The initial parameters that you need are:

%__________________________________________

% fobj = @YourCostFunction

% dim = number of your variables

% Max_iteration = maximum number of generations

% SearchAgents_no = number of search agents

% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n

% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n

% If all the variables have equal lower bound you can just

% define lb and ub as two single number numbers

% To run ALO: [Best_score,Best_pos,cg_curve]=ALO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)

% The Whale Optimization Algorithm

function [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj,handles,value)

% initialize position vector and score for the leader

Leader_pos=zeros(1,dim);

Leader_score=inf; %change this to -inf for maximization problems

%Initialize the positions of search agents

Positions=initialization(SearchAgents_no,dim,ub,lb);

Convergence_curve=zeros(1,Max_iter);

t=0;% Loop counter

% Main loop

while t<Max_iter

    for i=1:size(Positions,1)

        % Return back the search agents that go beyond the boundaries of the search space

        Flag4ub=Positions(i,:)>ub;

        Flag4lb=Positions(i,:)<lb;

        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;

        % Calculate objective function for each search agent

        fitness=fobj(Positions(i,:));

        All_fitness(1,i)=fitness;

        % Update the leader

        if fitness<Leader_score % Change this to > for maximization problem

            Leader_score=fitness; % Update alpha

            Leader_pos=Positions(i,:);

        end

    end

    a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)

    % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)

    a2=-1+t*((-1)/Max_iter);

    % Update the Position of search agents 

    for i=1:size(Positions,1)

        r1=rand(); % r1 is a random number in [0,1]

        r2=rand(); % r2 is a random number in [0,1]

        A=2*a*r1-a;  % Eq. (2.3) in the paper

        C=2*r2;      % Eq. (2.4) in the paper

        b=1;               %  parameters in Eq. (2.5)

        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)

        p = rand();        % p in Eq. (2.6)

        for j=1:size(Positions,2)

            if p<0.5   

                if abs(A)>=1

                    rand_leader_index = floor(SearchAgents_no*rand()+1);

                    X_rand = Positions(rand_leader_index, :);

                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)

                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)

                elseif abs(A)<1

                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)

                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)

                end

            elseif p>=0.5

                distance2Leader=abs(Leader_pos(j)-Positions(i,j));

                % Eq. (2.5)

                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);

            end

        end

    end

    t=t+1;

    Convergence_curve(t)=Leader_score;

    if t>2

        line([t-1 t], [Convergence_curve(t-1) Convergence_curve(t)],'Color','b')

        xlabel('Iteration');

        ylabel('Best score obtained so far');        

        drawnow

    end

    set(handles.itertext,'String', ['The current iteration is ', num2str(t)])

    set(handles.optimumtext,'String', ['The current optimal value is ', num2str(Leader_score)])

    if value==1

        hold on

        scatter(t*ones(1,SearchAgents_no),All_fitness,'.','k')

    end        

end

⛄ 运行结果

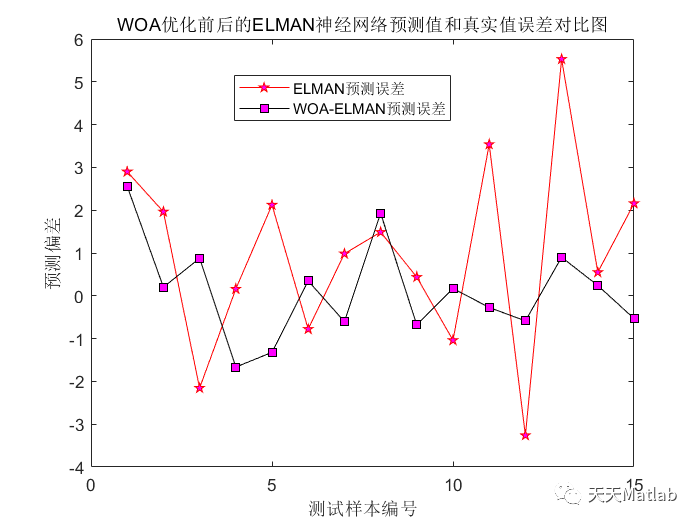
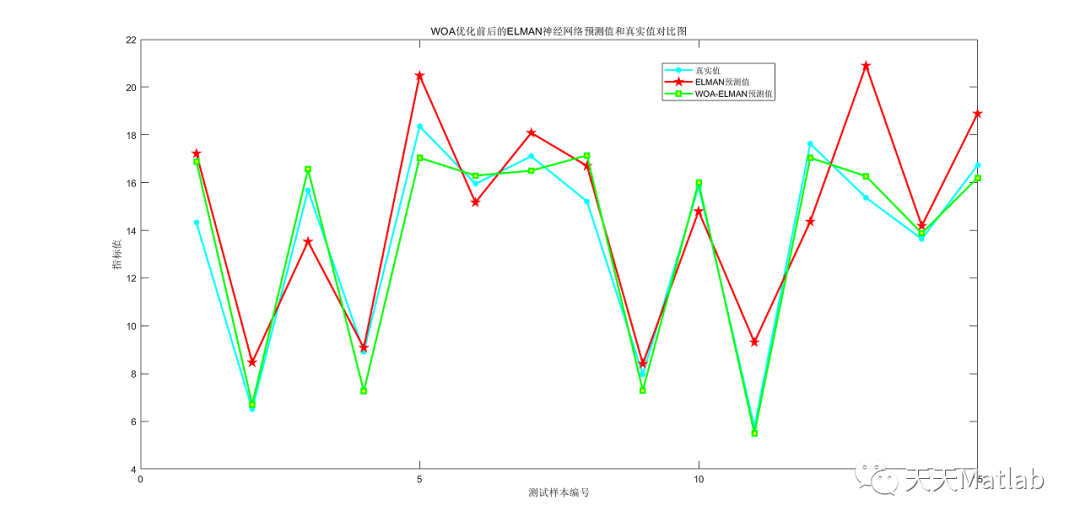
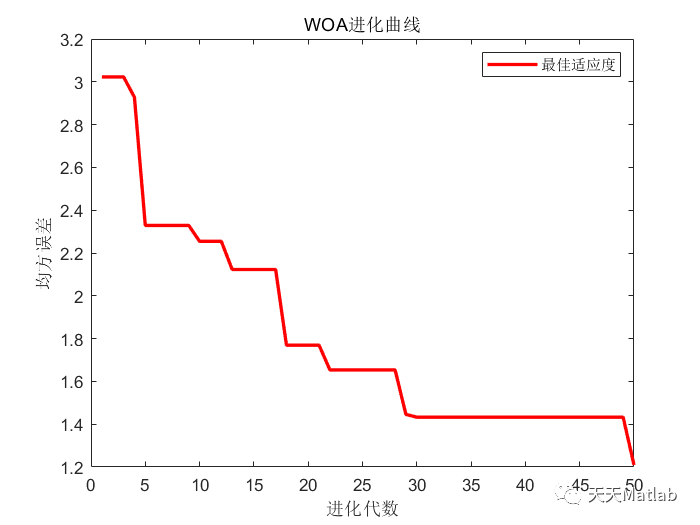
⛄ 参考文献

[1]吴丁杰, 温立书. 基于鲸鱼算法优化Elman神经网络的房价预测[J]. 长江信息通信, 2021, 34(10):3.

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料