
文章链接:
https://doi.org/10.1287/mnsc.2021.4182
01 研究背景
定价作为一种策略通常用于塑造市场需求,主要目标是了解产品价格如何影响n个产品的需求,并选择正确的价格以使卖方的总利润最大化。这个问题的关键困难之一是合理化不同产品之间的需求替代模式。过往研究侧重于使用基于随机效用最大化框架派生的特定离散选择模型来寻找产品定价问题的易处理实例,许多选择模型都会产生选择概率的封闭形式表示,从而让模型校准和价格优化问题变得易于处理。
但是,模型错误指定是一个重要的问题。例如,在混合Logit选择模型的估计中,必须预先确定消费者类型,并且企业通常需要对消费者市场有一定的了解才能得出适当的模型。如果价格优化模型中使用的需求模型指定错误怎么办?这是一个突出的问题,特别是当可用数据是不同产品价格下需求的嘈杂观察结果。
02 研究问题
本文的主要目标是开发一种数据驱动的定价方法,可以减轻校准需求模型时的模型错误指定问题,并确保对具有潜在价格约束的产品进行定价时的计算可处理性。
本文按如下方式解决模型指定错误问题:首先,不去假设特定的离散选择模型,而是构建一类具有可分离但通用凸扰动函数的代表性消费者模型,以实现模型识别问题的灵活性和价格优化问题的易处理性;其次,使用非参数方法来识别扰动函数,处理总需求数据。
03 模型分析
1.离散选择中的代表性消费者模型
考虑一个多产品定价问题,其中卖方提供的产品集用N={1,…,n}表示,{0}是外部选项。令产品j的价格为pj,xj(p)为给定价格向量p时选择产品j的概率。用vj表示产品j的确定性效用(不包括价格特征),α是价格敏感性参数。vj–αpj为产品j的基本效用,用uj表示。假设v0=p0=0(u0=0)作为外部选项。考虑以下确定性优化以获得选择概率x(p)
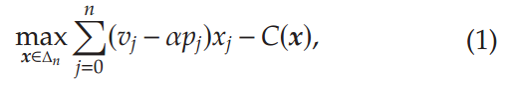
其中优化是针对定义为(2)的n维单位单纯形
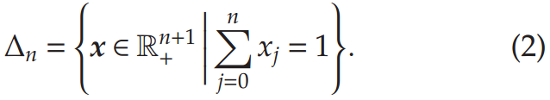
模型(1)提供了一种使用确定性优化模型在随机效用模型下计算选择概率的替代模型。在模型(1)中,消费者最优地选择了n个产品和外部选项的概率分布。消费者的整体效用被建模为预期基本效用与消费者选择的概率向量的一些非线性、确定性扰动函数C(·)的总和。假设扰动函数C(x)是凸函数(起到正则化函数的作用,并为选择多样化创造激励)。
对于任何随机效用选择模型,其效用函数是基本效用和随机噪声项(具有严格的正密度函数)之和,当凸扰动函数可分离时(即C(x)=ΣjCj(xj) ),我们有一个可分离的代表性消费者模型(SRCM)。SRCM使模型校准准确且定价问题易于处理。
2. 使用代表性消费者模型定价
多产品环境下卖方的预期利润最大化问题表述为

p是价格向量,x(p)是基于价格p的需求函数,其中产品的需求标准化为1。使用(1)中指定的代表性消费者的一般离散选择模型来对需求函数进行建模。
用Cj'(xj)来表示Cj(xj)–vjxj,从而只关注定价属性对选择替代的影响。
在可分离扰动函数下,(1)的最优性条件提供了价格和需求之间的封闭形式关系。将方程代入卖方的定价问题,定价问题简化为

其中w表示产品的成本向量。
【定理1】假设扰动函数满足以下条件:
1. 对于每个j=1,…,n,函数xCj'(x)是x中的凸函数。
2. 函数xC0'(1-x)是x的凹函数。
那么,定价问题(4)是需求x的凸优化问题,并且可以在多项式时间内计算最优价格。此外,如果最优解为x*,则最优定价策略为

3. 数据驱动的价格优化方法
假设给定一组产品价格、相应的需求(n 个产品)以及T个定价实验中外部选项的市场份额,获得的数据用{ptj,xˆtj} for t=1,…,T, j=1,…,n,表示,其中ptj和xˆtj 表示t时期产品j的观测价格和标准化需求。标准化需求根据每种产品的需求和外部选项计算,所有产品的标准化需求与外部期权的总和等于1。使用 xˆt0 表示外部期权在每个时期 t 的市场份额,并假设它在数据中可用。为了便于说明,设置价格敏感度参数α=1。
对于一组给定的价格p,用xC(p) 表示由扰动函数 C(·) 指定的 SRCM (1) 的相应理论需求。用 Cˆ (·) 来表示估计的扰动函数。
3.1识别问题
基于SRCM的最优性条件为扰动函数C(·)提供识别条件。
从以下条件推断真实函数C'(·):=(C1'(·),…,Cn'(·),C0'(·)):找到C—使得对于所有非负或数中的p=(p1,…,pn),有
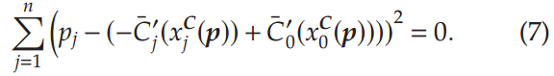
MI表示可接受的扰动函数的集合并包括基本事实C’。用xtj来表示 xC j (pt )。
3.1.1估计问题
考虑一个最小化与识别条件的偏差的估计问题

其中 ptj 和 xˆtj 表示t时期产品j的需求观测价格和噪声观测:即xˆtj=xtj+εtj。损失函数定义为实验价格中与(7)中识别条件的最坏偏差。
3.2价格优化
定价问题是找到 x 来最大化目标

求解估计模型(11)提供了每个采样点xˆtj处C'j(·)的拟合值。用 yˆtj 来表示估计模型的输出,即Cj'—(xˆtj))。使用这些值构建Cj'(x)的分段线性近似来优化产品的价格。
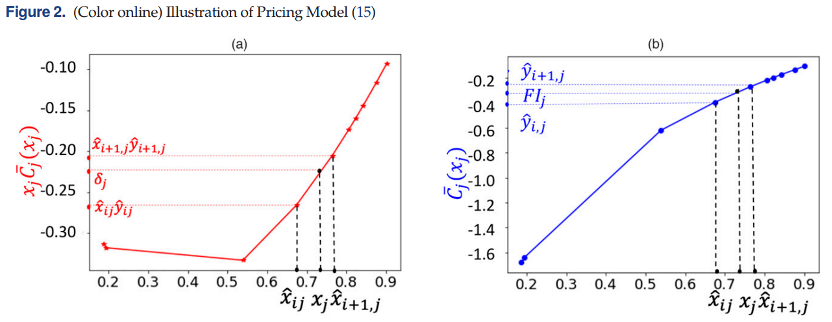
最终,优化问题可以建模为以下线性规划问题:

04 实验与结论
在实验验证部分,本文使用汽车数据、快餐数据等多种数据集将其提出的MDM框架与三种广泛使用的定价问题方法(消费者估值样本定价、离散选择模型和弹性模型)进行比较,获得了良好的性能表现。
总的来说,本文使用离散选择中的代表性消费者模型开发了一种数据驱动的方法来解决多产品定价问题。一方面,文章描述了定价问题变得易于处理的条件。另一方面,文章提出的代表性消费者模型通过可加性和可分离的扰动函数在价格和需求之间建立了一组封闭式关系,这些关系为识别扰动函数提供了条件。即使只有少量实验来测试不同定价决策的效果,也可以用来指导搜索最优定价解决方案。文章在两组行业数据上使用这种方法来表明,即使存在消费者异质性,该框架也能提供合理的价格建议。
微信公众号后台回复
加群:加入全球华人OR|AI|DS社区硕博微信学术群
资料:免费获得大量运筹学相关学习资料
人才库:加入运筹精英人才库,获得独家职位推荐
电子书:免费获取平台小编独家创作的优化理论、运筹实践和数据科学电子书,持续更新中ing...
加入我们:加入「运筹OR帷幄」,参与内容创作平台运营
知识星球:加入「运筹OR帷幄」数据算法社区,免费参与每周「领读计划」、「行业inTalk」、「OR会客厅」等直播活动,与数百位签约大V进行在线交流

文章须知
文章作者:东南数智港
责任编辑:张琪 马玺渊
微信编辑:疑疑
文章由『运筹OR帷幄转载发布
如需转载请在公众号后台获取转载须知
关注我们
FOLLOW US


内容中包含的图片若涉及版权问题,请及时与我们联系删除







评论
沙发等你来抢