近期，与华南理工苏楚鹏博士合作，在国际权威期刊《Applied Soft Computing》发表了一篇基于图神经网络和深度强化学习求解动态作业车间调度问题的文章《 Evolution strategies-based optimized graph reinforcement learning for solving dynamic job shop scheduling problem》。今天就文中的主要内容和大家做一次分享，也欢迎大家提出建设性意见。在公众号后台回复“图动态”获取全文。

Part1摘要

具有动态事件和不确定性的作业车间调度问题是一个强NP难的组合优化问题，在制造系统中有着广泛的应用。近年来，利用机器学习技术解决JSSP问题逐渐成为主流方法。然而，大多数现有技术不能处理动态事件并且几乎不考虑不确定性。为此，本文提出了基于图神经网络（GNN）和深度强化学习（DRL）的动态JSSP（DJSP）求解框架，以处理机器故障和随机加工时间。首先，将DJSP表达为马尔可夫决策过程（MDP），使用析取图表达状态；其次，提出了一种基于GNN的模型，通过考虑动态事件的特征和问题的随机性，例如机器故障和随机加工时间，有效地提取状态的嵌入；然后，该模型基于学习到的嵌入，通过将最优工序分派到机器作来构造调度解；值得注意的是，我们提出使用进化策略（ES）来代替传统的强化学习算法，从而获取更稳定、更强大的最优策略。大量的实验表明，我们的方法大大优于现有的基于强化学习的方法和传统的方法在多个经典的基准测试。

Part2析取图模型

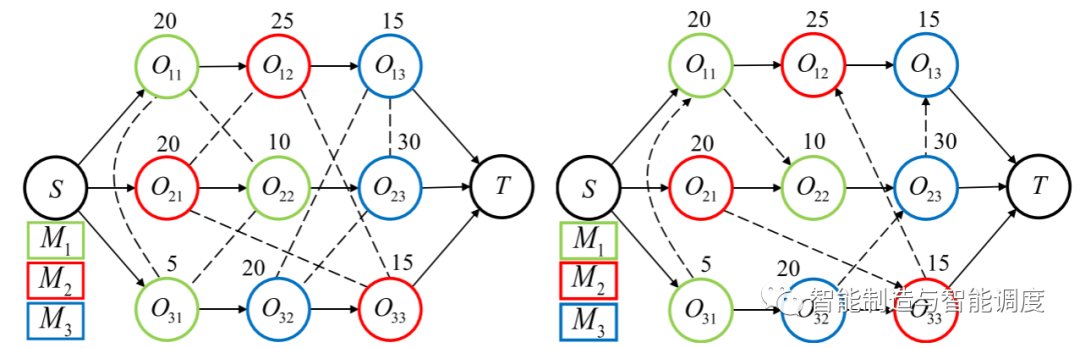
析取图模型是描述JSP调度过程和结果的一种重要图结构表示方式。析取图G=(O,C,D)，O表示所有工序组成的节点集，一个节点代表一个工序，其中包括两个虚拟节点S和T，表示虚拟的起始工序和终止工序，这些虚拟节点的加工时间为零。C是连接工序间的有向弧集，表示同一个工件的工序之间的先后加工顺序约束。D是连接可以在同一台机器上加工的工序间的析取弧集。基于析取图的调度过程就是将每一条无向析取弧转换为有向析取弧，图1展示了一个3x3 的JSP未解决时的析取图（左），以及该JSP的一个解决方案的析取图（右）。在本研究中，在采用DRL解决JSP时，我们会将JSP Instance的信息转化为析取图，作为马尔可夫决策过程的状态，并根据任务调度及执行情况实时更新。

析取图本质上为一种图结构，因此可以很自然地想到使用图神经网络来处理这类问题，从而充分利用潜在的图信息。

Part3调度框架

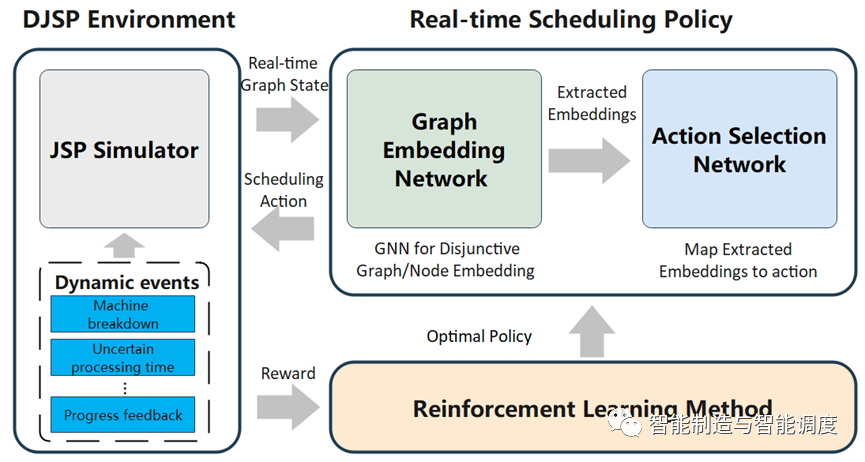
为了解决JSP，提出一种基于GNN和DRL的JSP调度框架，如图2所示。该框架由三部分组成，JSP 环境、调度策略和强化学习模块，JSP环境可以加入随机生成机器故障、不确定加工时间等干扰，以模拟DJSP环境。调度策略进一步分成图嵌入网络和动作选择网络。在调度决策时，JSP环境将实时析取图作为状态发送到调度策略，调度策略使用GNN提取实时析取图的节点/图嵌入特征，并发送到动作选择网络，动作选择网络选择动作反馈到JSP环境，选择到的工序分配给机器。当调度完成后，收集调度过程中的动作和奖励等信息，用于强化学习模块训练调度策略。最后，优化后的调度策略可用于求解不同的JSP Instance，以获得满意的解决方案。

Part4基于DRL和GNN的实时调度

4.1马尔科夫决策过程

使用DRL解决调度问题的关键是将调度问题转化为MDP，MDP定义了状态、状态转换、动作和奖励函数。我们以JSSP实时析取图作为状态和GNN作为状态特征提取器，并制定以下的MDP模型来求解JSSP。值得注意的是，本研究采用进化策略作为训练算法，使用适应度函数作为反馈来更新DRL模型。为了方便起见，在训练算法的部分中定义了适应度函数（其可以被视为奖励函数）。

图状态表达

DJSP环境在决策步骤k时的状态是一个实时析取图，是一个包含动态和静态信息有向同质图；其中，包含在步骤k之前确定了方向的有向析取弧，表示已被调度的工序的加工顺序关系; 是所有节点（工序）在k步骤时包含的特征信息，对于每一个，我们添加了以下特征：

• 节点类型：-1表示未被调度， 1表示已完成，0表示工序已被安排到机器上，不管机器是否能正常工作。
• 加工时间：完成工序所需要的加工时间。在求解静态JSP时，该特征始终为。当考虑不确定加工时间干扰时，工序加工时间在完工前为，完工后为。
• 等待时间：工序的等待时间，工序准备去加工到开始加工的时间，即完工后，到被加载到机器所经历的时间。
• 剩余操作数：工序后续操作数。
• 完成率：此工序完成后，占整个工件的完成率。

状态转移

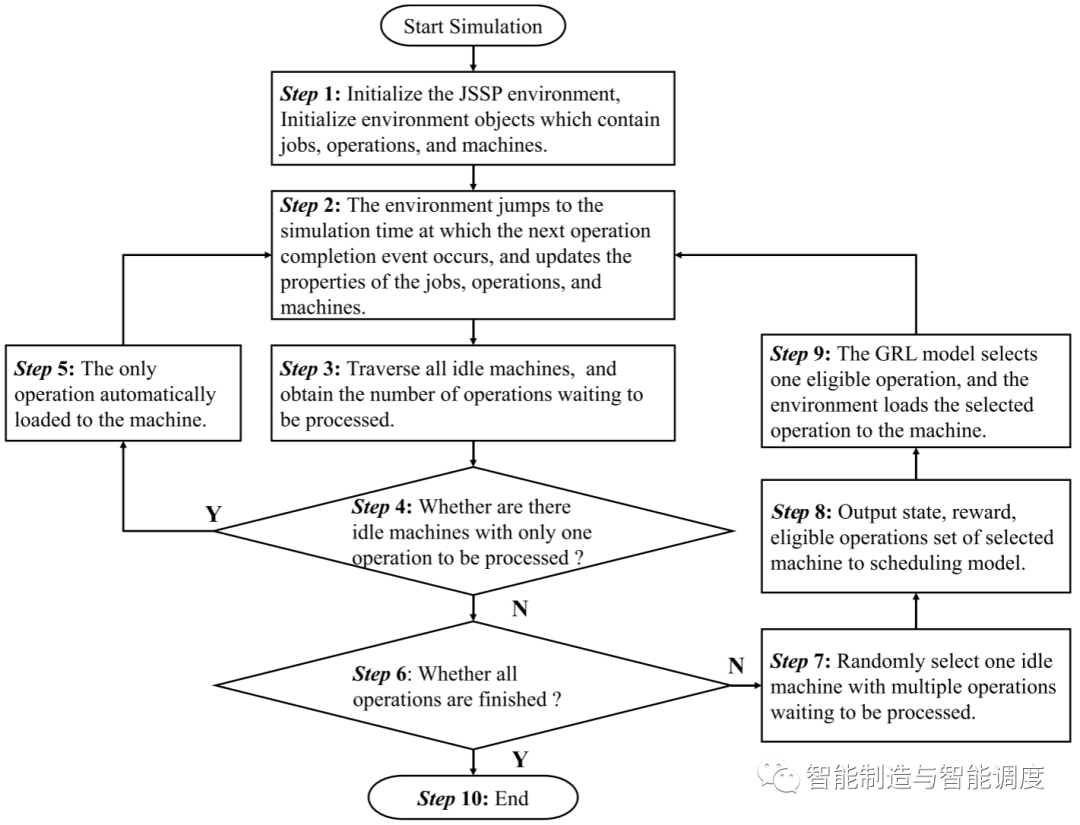
每一次工序完工安排到机器时，会造成状态转移，并生成一个新的实时析取图。图3和图4给出了一个示例：仿真时间20<<25时，工序，正在加工，如图4.(a)所示。当仿真时间t_sim到达25时，，完工，机器, 空闲且有待加工的工序；因机器只有一个待加工工序，DJSP环境自动安排工序到机器上，转移到新的状态，如图(b)所示。机器有，两个待加工的工序，即在处在动作空间有，两个可选动作；选择作为机器的下道工序，因此，之间的析取弧方向为，新的状态如图3.(c)所示。由上可知，仿真时间=25时DJSP环境调度了两道工序，造成了两次状态转移，所以、的开始加工时间都为25。

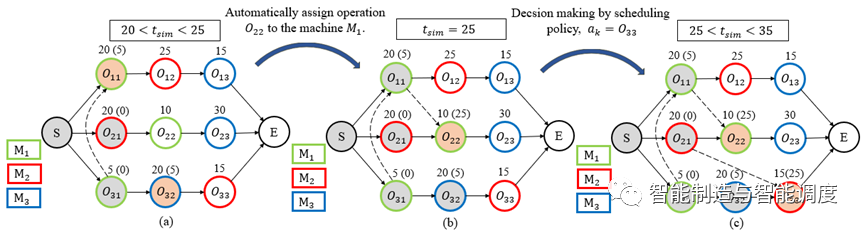
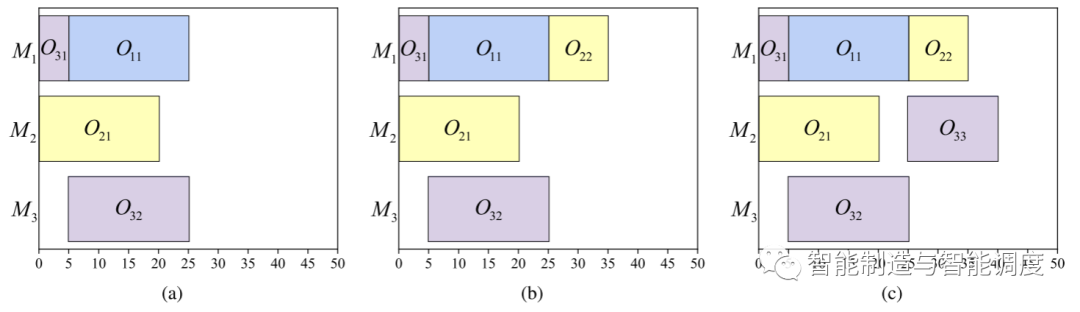
动作选择

在决策步骤, 调度策略需要为一台空闲机器分配工序/动作，可选工序将按照下图中的step7~step9确定。

4.2策略

图嵌入

我们采用了图同构网络（GIN）提取析取图和节点特征。GIN 是一种衍生自 GNN 的体系结构，被证明具有很强的鉴别能力，相比 GCN、GAT 等图神经算法，通过引入多层感知机（Multi-layer perceptron, MLP）等，强调了对图计算的单射性，能够更好的处理图的特征。每个节点的嵌入可按照下式进行计算：

GIN执行L次更新迭代后，获得每个节点的p维嵌入；将得到的各个节点的特征表示通过求平均后得到整张图图嵌入表征向量:

工序选择

调度工序选择过程如下：

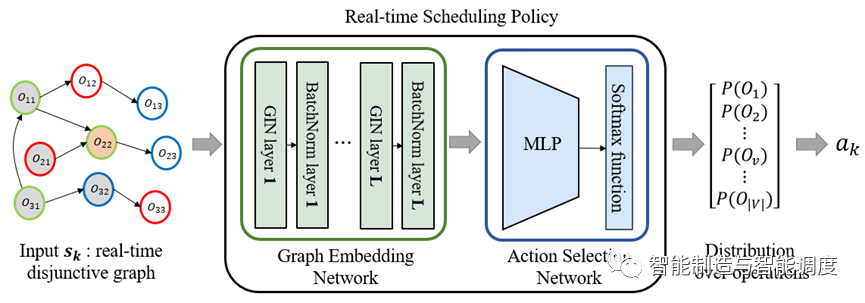
在决策时刻k, GNN提取析取图的节点嵌入和图嵌入，组合形成矩阵：

将输入到动作选择网络计算调度动作，采用MLP计算每一个工序的分数：

然后应用softmax函数计算工序分数的分布:

一般来说，在训练中，从 中采样获得动作（采样方式）；在测试中，贪婪地选取中概率最大值作为动作（贪婪方式）。而本文中我们因为采用了ES作为训练方法，所以在训练和测试阶段均采用了贪婪方式。在计算前，需将非法工序屏蔽掉；通过赋予非法动作集合的工序分数为-∞，使得等于0，达到屏蔽非法动作的目的。

Part5学习算法

5.1进化策略

我们采用OpenAI-ES算法训练提出的模型，它被证明可以替代流行的RL算法，其梯度近似计算和参数更新方法如下：

采用ES优化调度策略有如下优点，一方面，算法易于并行化，高鲁棒，更出色的探索能力；另一方面，最终要优化的目标（在本研究中，为最大完工时间）可作为适应度函数F(∙)，这样减少了奖励函数设计的工作量，也避免了贡献度分配的问题。

5.2适应度函数设计

调度策略求解JSP的目标是最小化最大完工时间，与适应度函数呈相反关系，因此衡量调度策略表现的适应度函数可以定义为:

为了能够客观地评价各种不同规模的案例，采用如下的归一化方法：

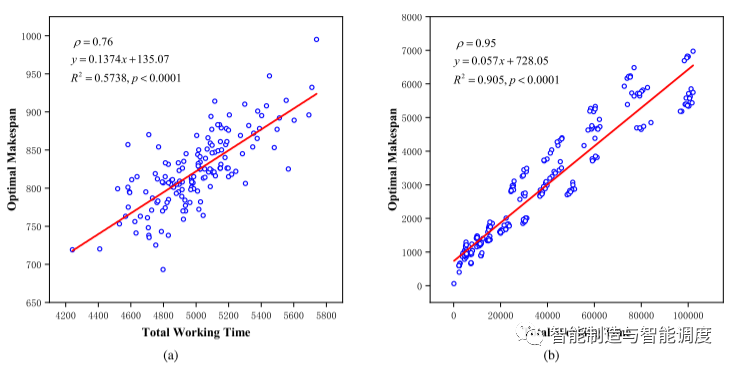
其中是最优makespan。

我们开展了实验对P与进行相关性分析，以证明适应度函数中近似的合理性。

5.3基于ES的训练过程

完整的训练过程如下所示。

Part6实验

6.1实验配置

Dataset。在本研究中，从OR库中选择了一些标准实例来初始化调度环境。

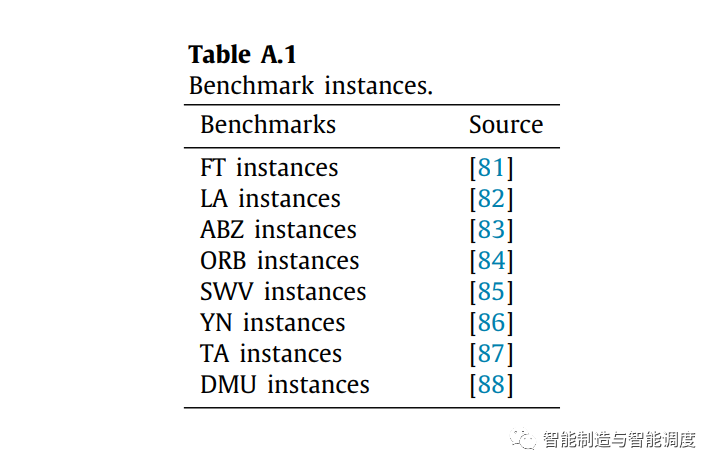
Baselines。静态试验选取了8种启发式规则、两种遗传算法、L2D、GNN Scheduler、ScheduleNet和DDDQNPR（基于深度强化学习的自适应车间调度问题研究）作为baseline。动态试验中仅选取了8种启发式规则。

性能评估。在静态实验中，通过相对调度误差（也叫做gap）来评估不同调度方法的性能：

6.2训练细节

相关超参数如下：

6.3静态案例上的性能评估

验证集结果

为了验证模型训练效果，随机生成100个instance作为验证集，可以看出，所提出的GRL模型比所有PDR提供了更好的调度解。

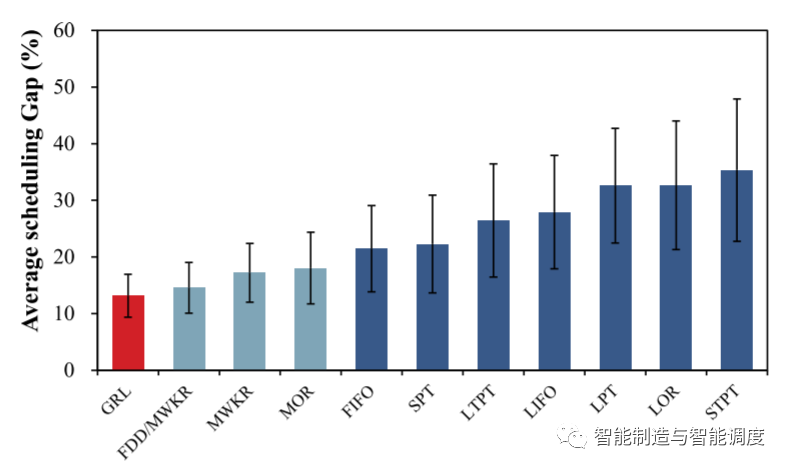
benchmark案例的比较结果

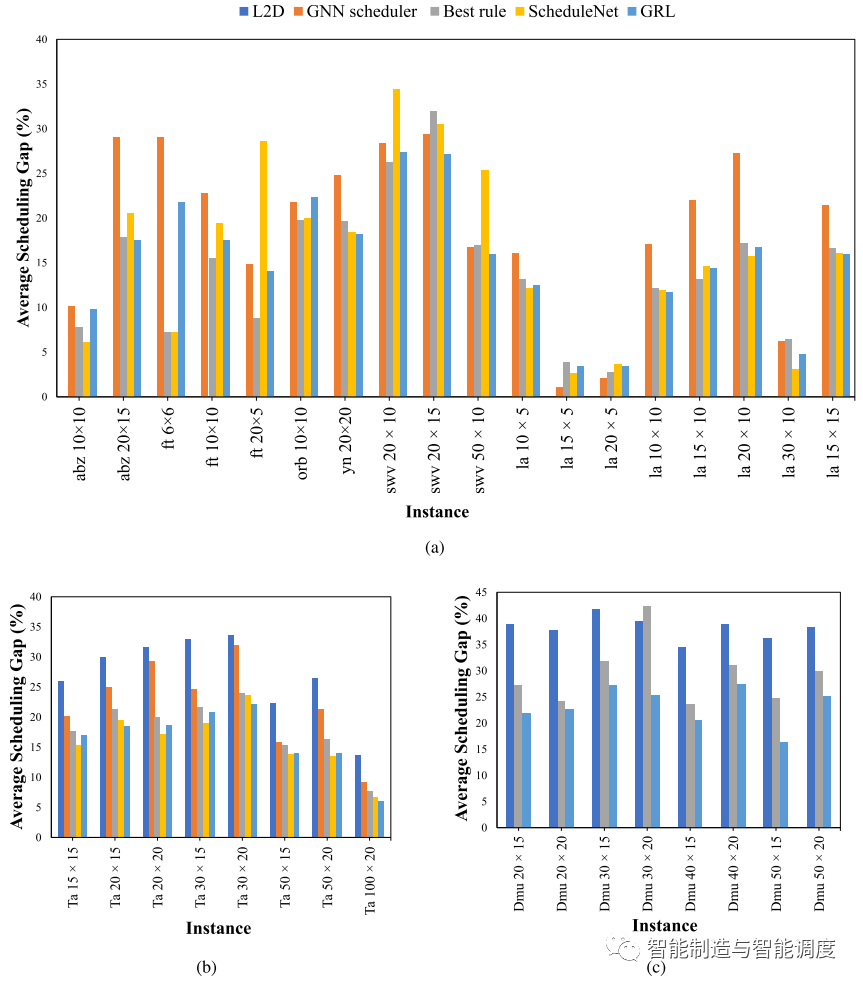
下图为所提出的GRL方法与其他规则和DRL方法的对比，可以看出：（1）在不同的基准测试集上，由于JSSP案例的特点和难度不同，调度方法的结果也有很大差异；(2)所提出的GRL方法在大多数测试集上优于L2D，GNN Scheduler和PDR，特别是在大规模的实例集，如TA和DMU；(3)所提出的GRL方法与ScheduleNet性能接近。

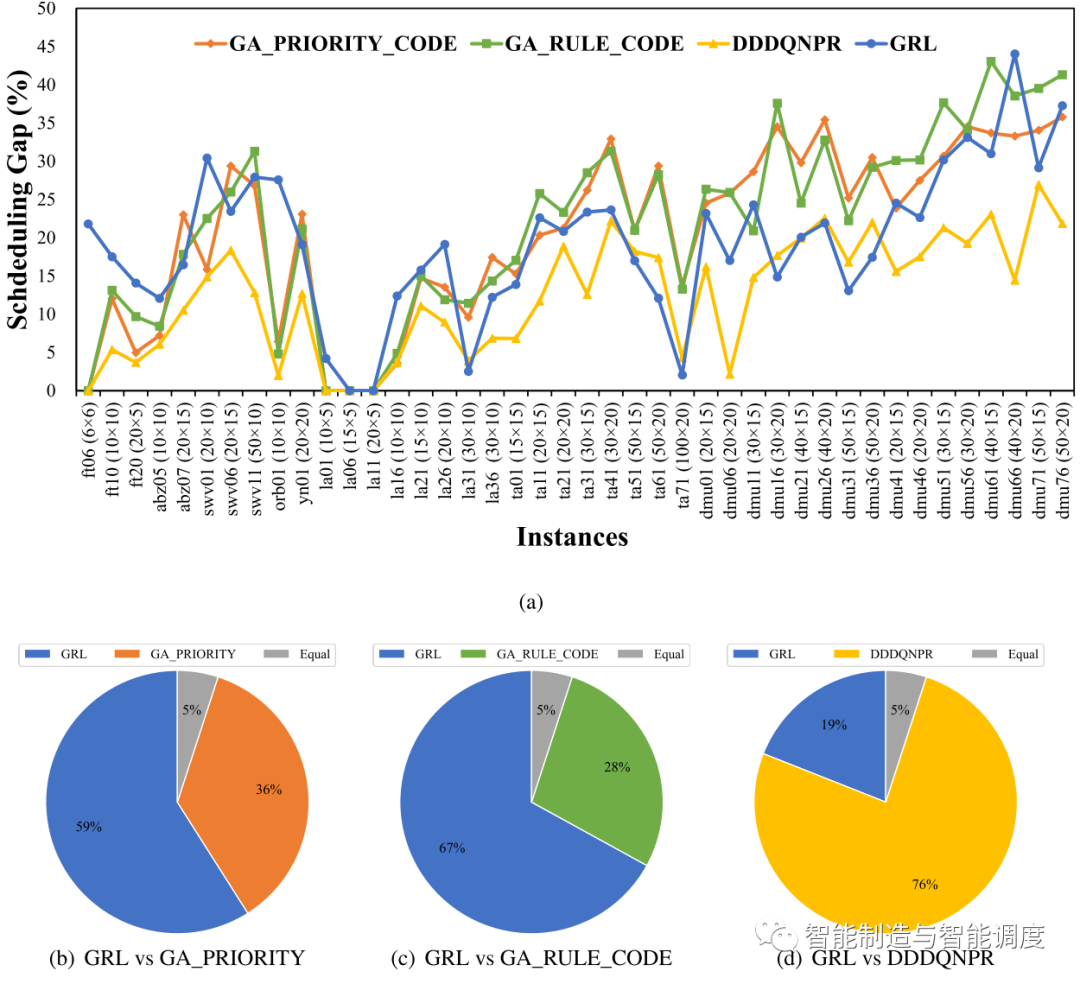
下图为所提出方法与元启发式和DDDQNPR测试结果的比较。可以看出：（1）在大多数案例上，GRL优于两种元启发式；（2）GRL在76% instance上差于DDDQNPR，在24% instance上优于或等于DDDQNPR；然而，值得注意的是，DDDQNPR是通过instance-by-instance训练的，训练集和测试集的测试数据分布一致，这是DDDQNPR的求解效果较优的重要原因之一。

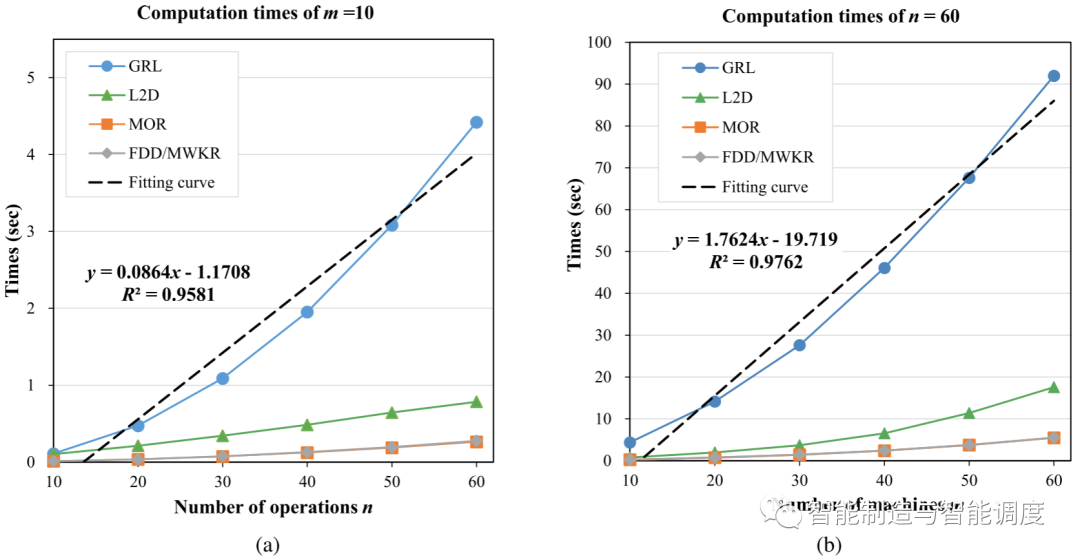
6.4计算复杂度分析

为了验证所提出的GRL方法可以满足JSP实时调度的时间限制要求，我们研究GRL在不同规模的JSP instance 中的计算复杂性。

6.5动态扰动下的实时调度性能评估

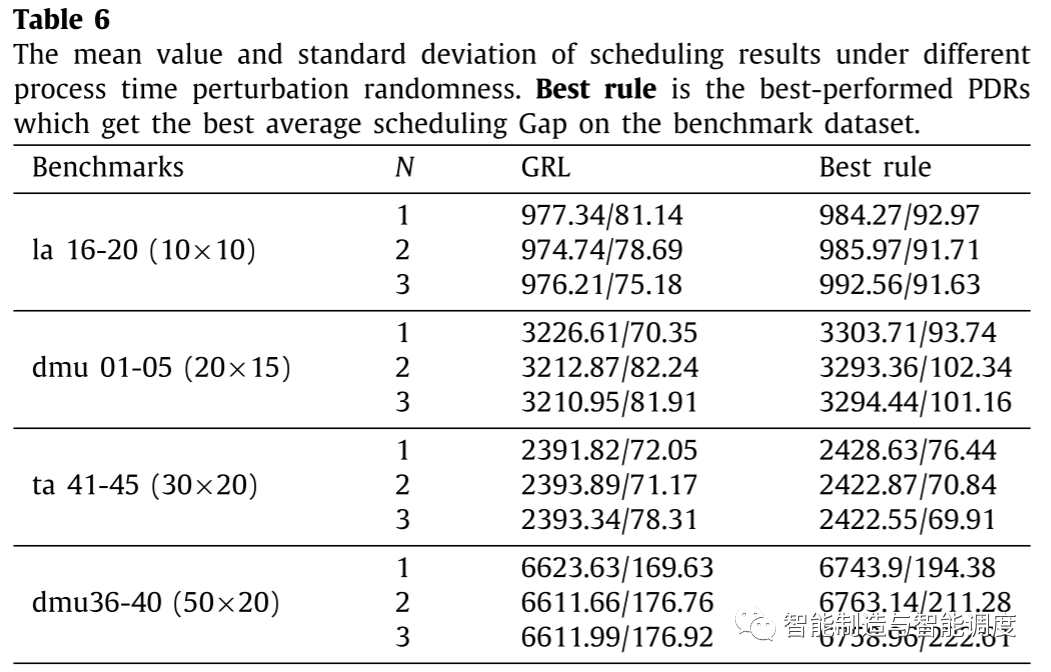
我们在加入随机加工时间，机器故障等干扰的动态实时JSP上进行进一步的实验以测试GRL方法的鲁棒性。

从下表中可以看出，在所有规模的调度问题上，GRL性能都强于PDR，这意味着GRL在加入随机加工时间干扰的动态实时调度环境下具有鲁棒性。

从下表可以看出，GRL可以获得比PDR更好的调度结果，这证明了GRL在解决加入机器故障干扰的动态实时调度问题上的有效性。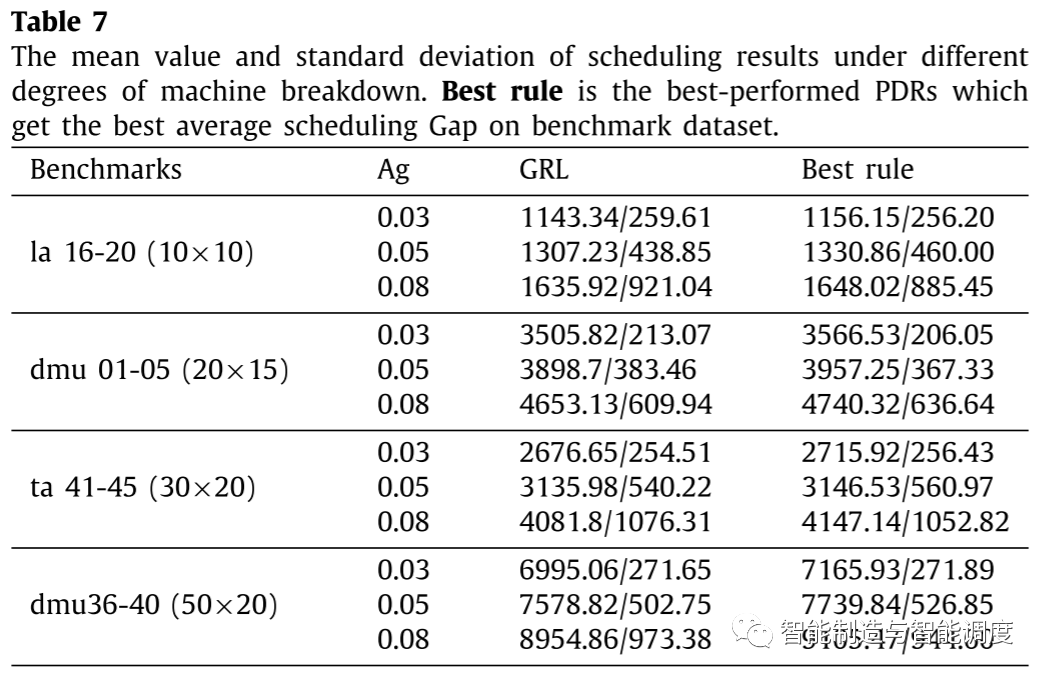

6.6消融实验

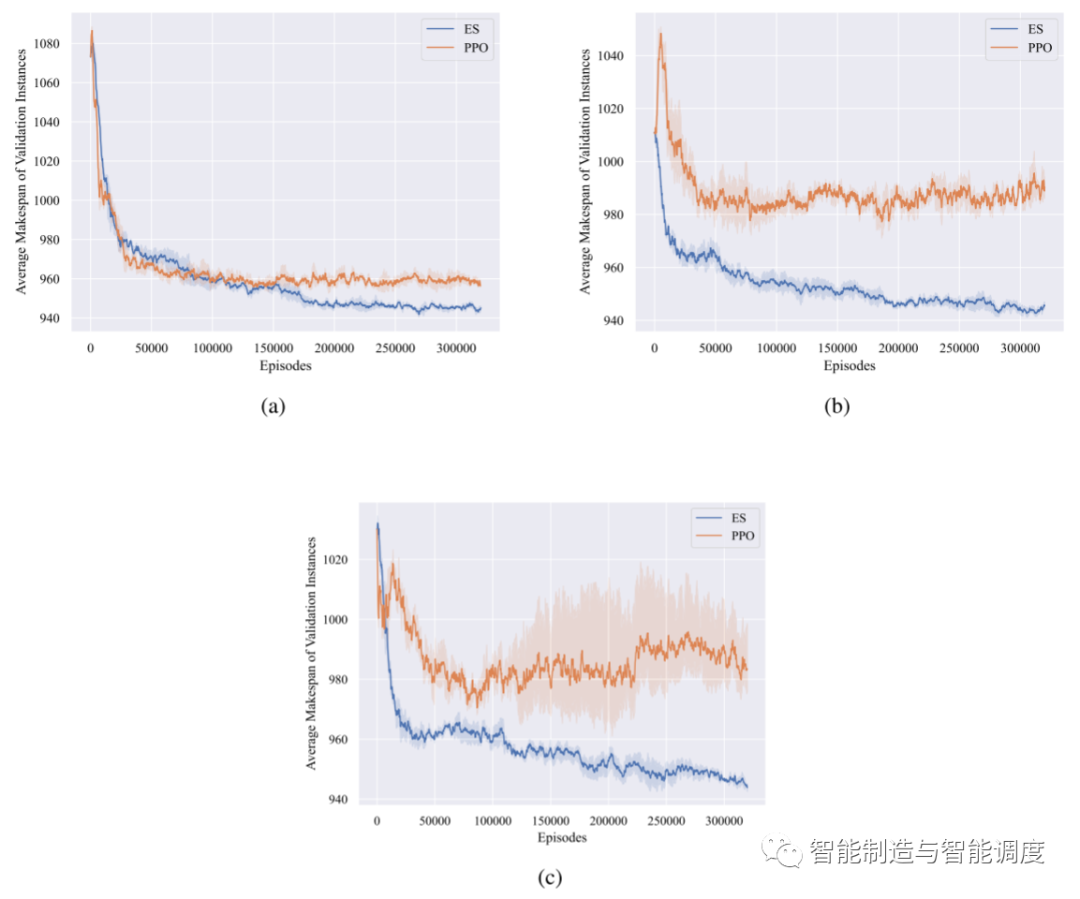
为了验证所提出的基于ES的训练算法在JSSP上的优越性，我们进行了消融实验，比较了其与PPO的性能。

如下图所示，可以看出：（1）首先，ES算法能获得较好的Makespan，表现出较强的探索能力。（2）此外，ES算法的训练时间比PPO少得多。原因是ES算法和PPO算法在相同的代数后收敛，但ES算法不需要进行反向传播，也不需要值函数。（3）最后也是最重要的是，ES算法比PPO算法更鲁棒。

参考文献：Su C, Zhang C, Xia D, et al. Evolution strategies-based optimized graph reinforcement learning for solving dynamic job shop scheduling problem[J]. Applied Soft Computing, 2023, 145: 110596.