关键词：凝聚态物理，非平衡量子物理，量子多体系统，非平衡动力学，本征态热化假说



论文题目：
Unified Theory of Local Quantum Many-Body Dynamics: Eigenoperator Thermalization Theorems
论文地址：
https://journals.aps.org/prx/abstract/10.1103/PhysRevX.13.031013

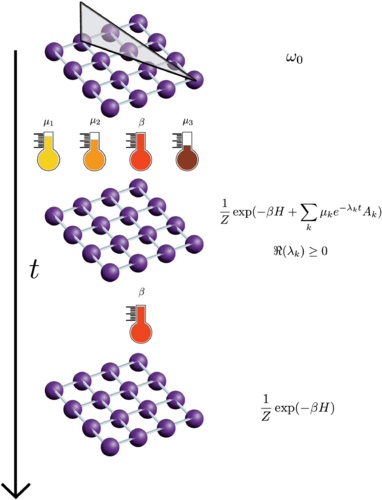
计算局部相互作用量子多体系统的非平衡动力学是物理学的一个基本挑战，其应用范围广泛涵盖从凝聚态物理到量子信息处理。大多数这些系统都无法用任何解析方法来处理，数值计算仅限于小系统和短时间尺度。本文在一个新近发展的严格理论中统一了所有这些可能系统的动力学，并展示了一个违背直觉的结果：量子多体系统始终处于平衡状态，但具有时变的化学势，这允许对长时间动力学获得解析解。

本征态热化假说（eigenstate thermalization hypothesis，ETH）一直是非平衡量子物理的理论基础。然而，ETH 不仅从未得到证明，而且已知有几种模型是其“强”版本的反例。这项研究证明了 ETH 的“弱”版本，即动力学的时间平均值在某种意义上是“热化”的，并展示了可观测量的时间平均值由平衡态给出。

在 ETH 之外，作者还证明了有限频率下的动力学由同样处于有限频率的广义局部守恒律给出。此外，系统的状态始终是由这些守恒律定义的平衡态。这解析地解决了本来难以处理的混沌模型的动力学。

该理论可应用于量子多体疤痕（quantum many-body scars）*，连续、离散和耗散时间晶体、希尔伯特空间分段（Hilbert space fragmentation）、格点规范理论，以及无杂质局域化（disorder-free localization）等情况。

这项工作为研究非平衡量子系统提供了一个基本而严格的框架，涵盖了众多可能的研究方向，从设计新颖的量子纠错算法，到将用于平衡态物理的现有强大理论推广到非平衡情境。

*参考综述文章：Quantum many-body scars and Hilbert space fragmentation: a review of exact results. Sanjay Moudgalya et al 2022 Rep. Prog. Phys. 85 086501DOI 10.1088/1361-6633/ac73a0

图1. 非平衡量子多体动力学示意图。



编译｜梁金

量子信息与量子计算预读班



详情请参见：

量子信息与量子计算预读班：追踪量子信息革命交叉前沿



推荐阅读

‍1. 量子联结：高能物理、凝聚态物理和量子信息之间的联系
2. 具有张量网络的强化学习进行自纠错量子多体控制｜Nat. Mach. Intell. 速递
3. 解码薛定谔的猫：量子物理和人工智能的新颖交叉
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 加入集智学园VIP，获得20周年“涌现”学术年会入场券！
6. 加入集智，一起复杂！


点击“阅读原文”，填写报名表单

内容中包含的图片若涉及版权问题，请及时与我们联系删除