前言 旋转位置编码(Rotary Position Embedding,RoPE)是论文 Roformer: Enhanced Transformer With Rotray Position Embedding 提出的一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。而目前很火的 LLaMA、GLM 模型也是采用该位置编码方式。和相对位置编码相比,RoPE 具有更好的外推性,目前是大模型相对位置编码中应用最广的方式之一。
作者:绝密伏击
单位:奇虎360高级算法专家
备注:什么是大模型外推性?
外推性是指大模型在训练时和预测时的输入长度不一致,导致模型的泛化能力下降的问题。例如,如果一个模型在训练时只使用了 512 个 token 的文本,那么在预测时如果输入超过 512 个 token,模型可能无法正确处理。这就限制了大模型在处理长文本或多轮对话等任务时的效果。

旋转编码RoPE
1.1 基本概念
在介绍 RoPE 之前,先给出一些符号定义,以及基本背景。
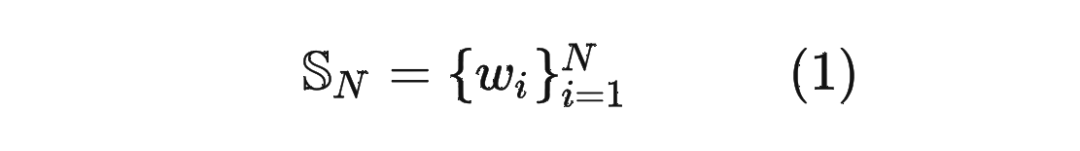
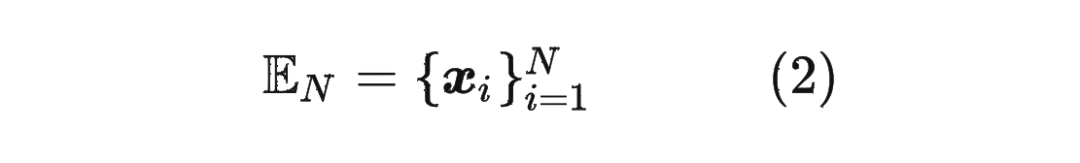
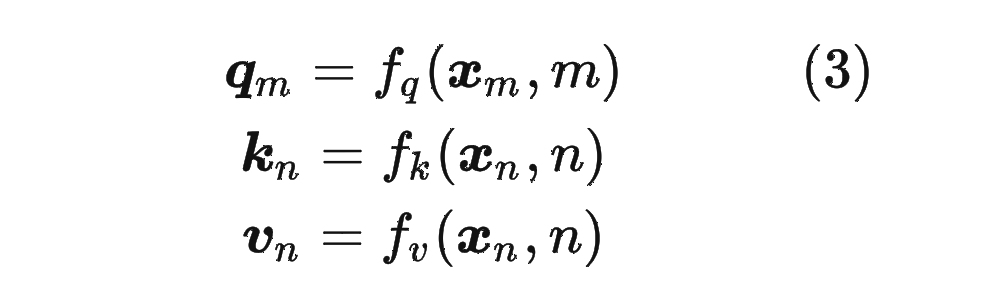
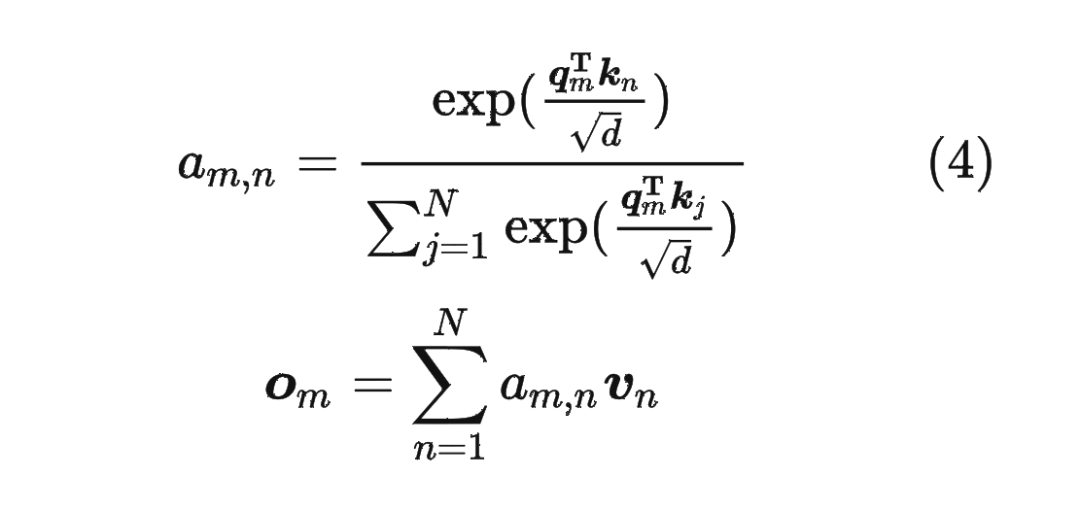
1.2 绝对位置编码
对于位置编码,常规的做法是在计算 query,key 和 value 向量之前,会计算一个位置编码向量 加到词嵌入 上,位置编码向量 同样也是 维向量,然后再乘以对应的变换矩阵 :
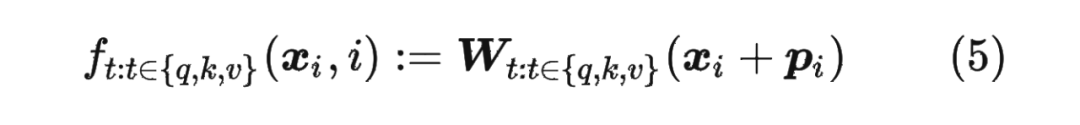
而经典的位置编码向量 的计算方式是使用 Sinusoidal 函数:
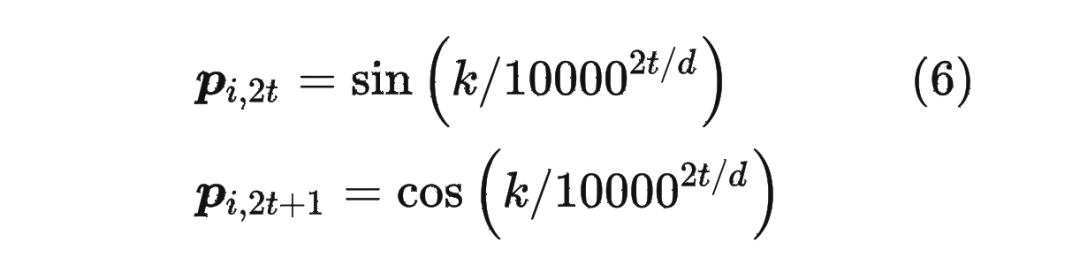
其中 表示位置 维度向量 中的第 位置分量也就是偶数索引位置的计算公式,而 就对应第 位置分量也就是奇数索引位置的计算公式。
1.3 2维旋转位置编码
论文中提出为了能利用上 token 之间的相对位置信息,假定 query 向量 和 key 向量 之间的内积操作可以被一个函数 表示,该函数 的输入是词嵌入向量 , 和它们之间的相对位置 :
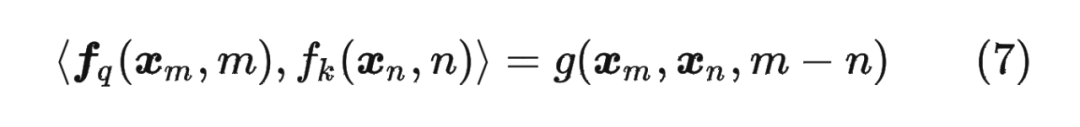
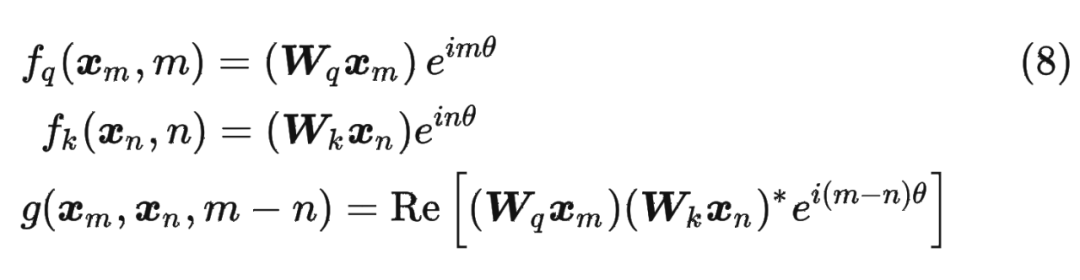
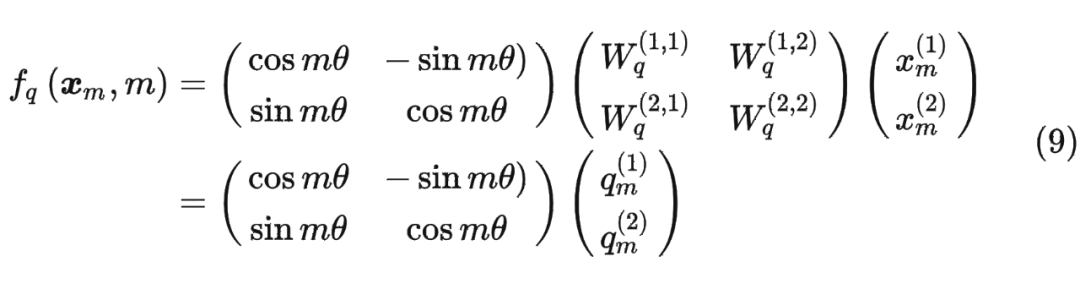
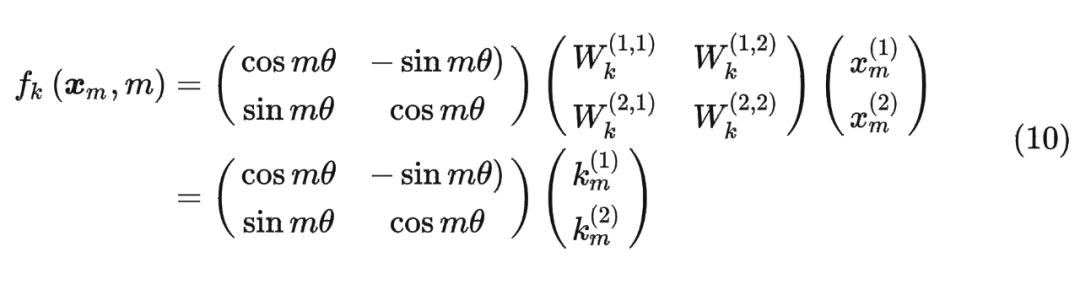
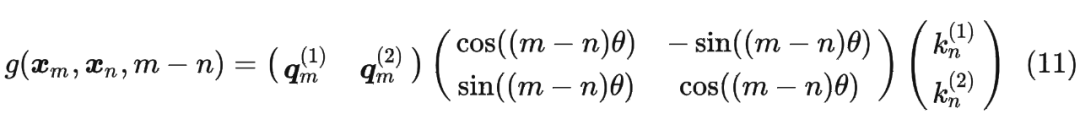
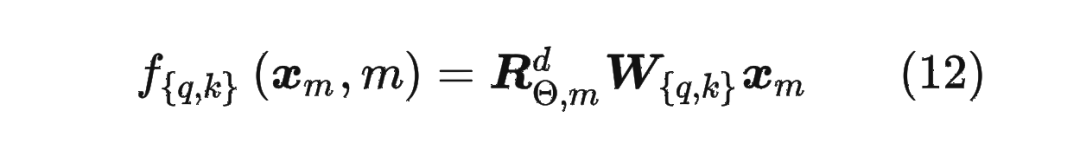

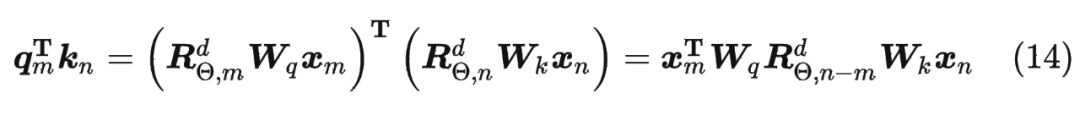
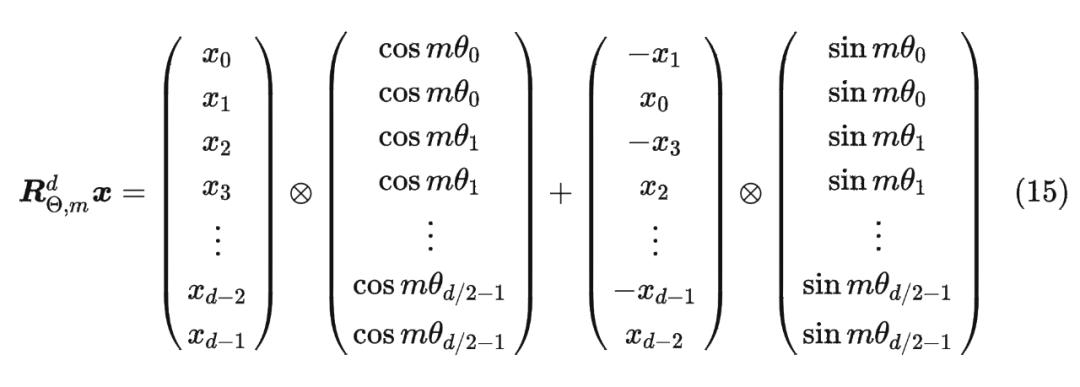
其中,。
1.6 远程衰减
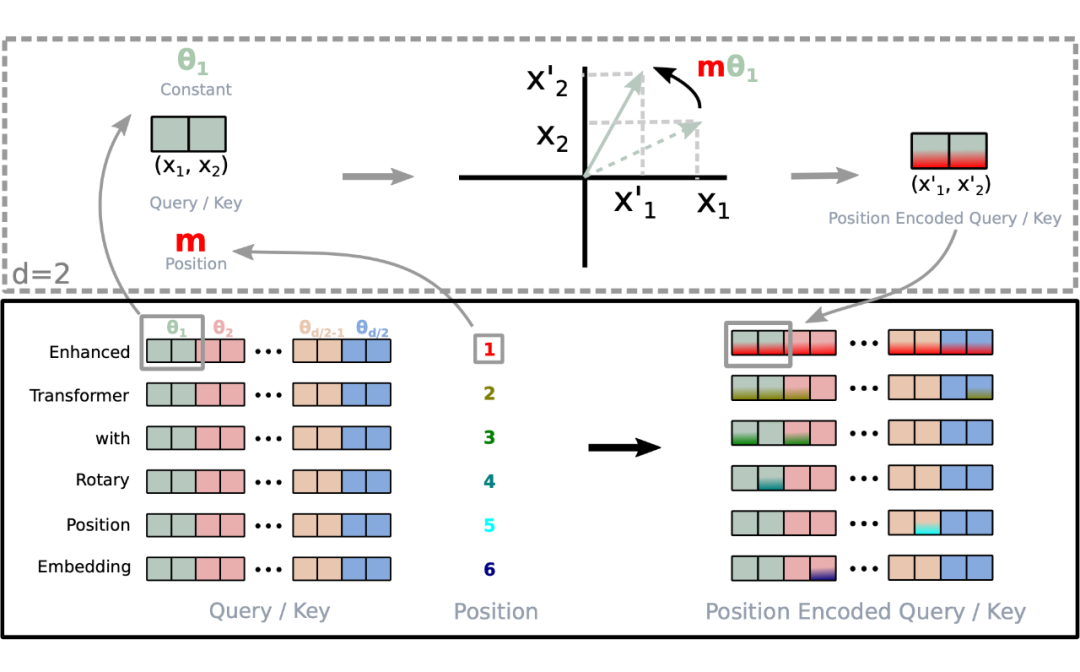
可以看到,RoPE 形式上和前面公式(6)Sinusoidal 位置编码有点相似,只不过 Sinusoidal 位置编码是加性的,而 RoPE 可以视为乘性的。在 的选择上,RoPE 同样沿用了 Sinusoidal 位置编码的方案,即 ,它可以带来一定的远程衰减性。
具体证明如下:将 两两分组后,它们加上 RoPE 后的内积可以用复数乘法表示为:
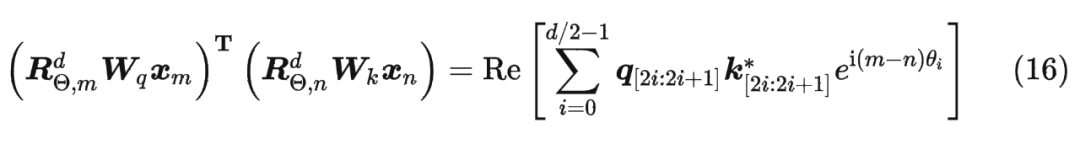
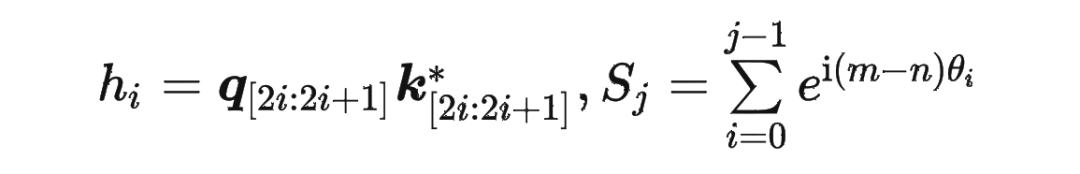
并约定 ,那么由 Abel 变换(分部求和法)可以得到:
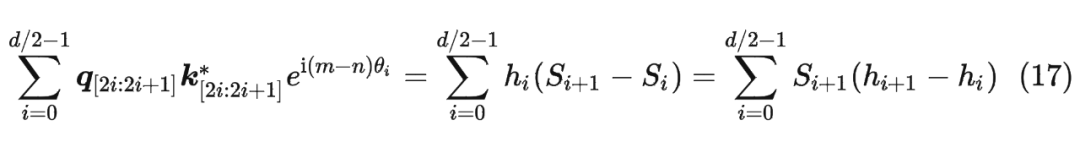
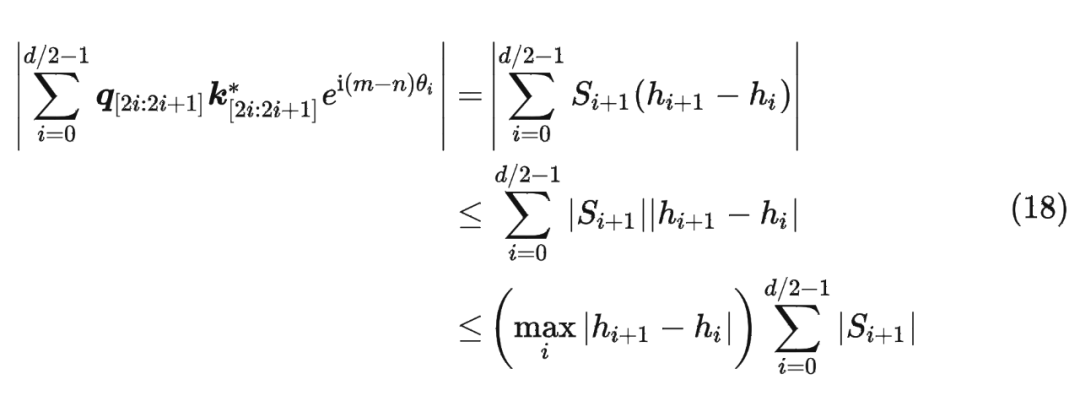
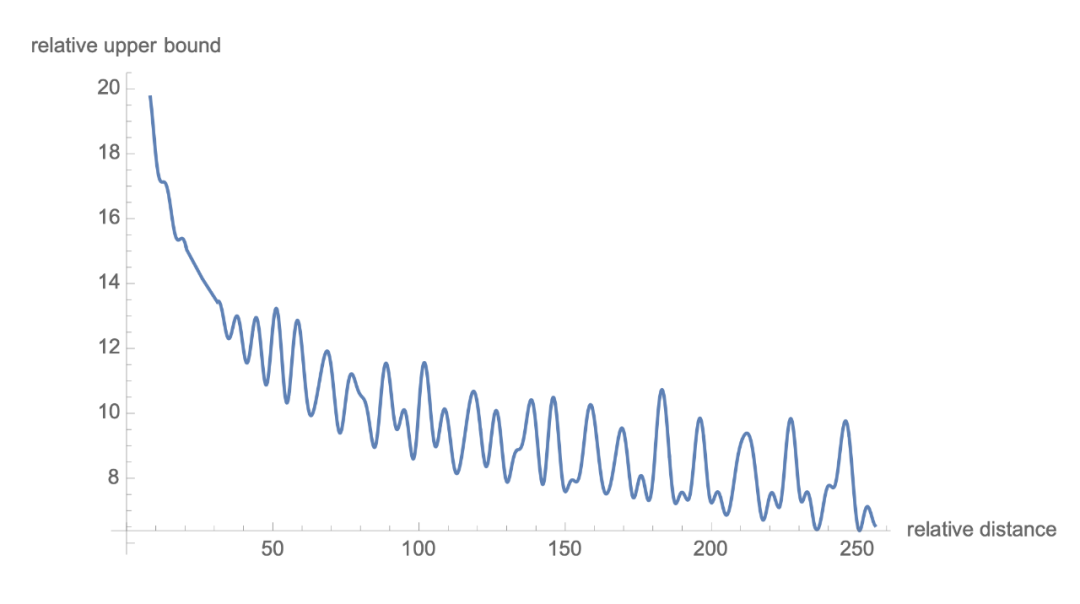

RoPE实验
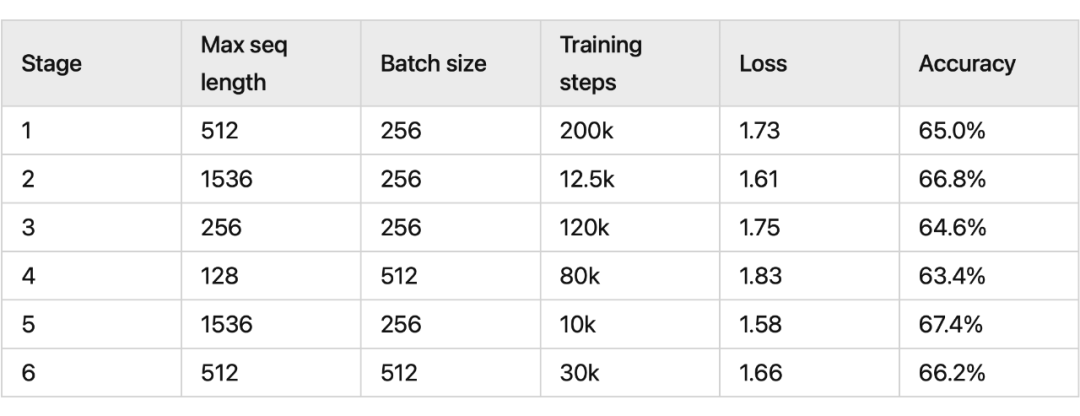
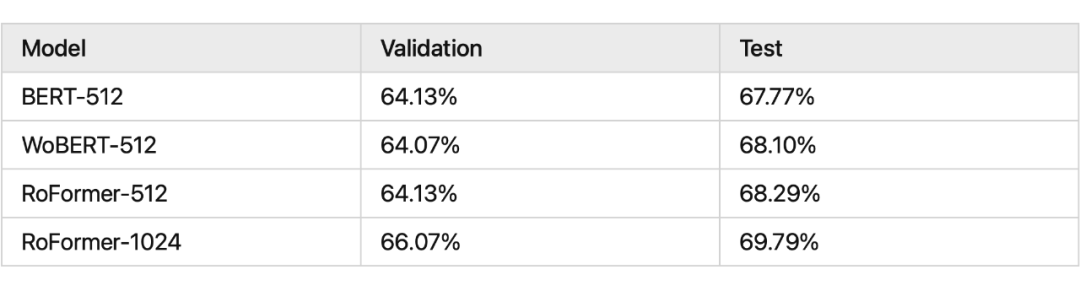

RoPE代码实现
3.1 在LLAMA中的实现
# 生成旋转矩阵
def precompute_freqs_cis(dim: int, seq_len: int, theta: float = 10000.0):
# 计算词向量元素两两分组之后,每组元素对应的旋转角度\theta_i
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
# 生成 token 序列索引 t = [0, 1,..., seq_len-1]
t = torch.arange(seq_len, device=freqs.device)
# freqs.shape = [seq_len, dim // 2]
freqs = torch.outer(t, freqs).float() # 计算m * \theta
# 计算结果是个复数向量
# 假设 freqs = [x, y]
# 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]
freqs_cis = torch.polar(torch.ones_like(freqs), freqs)
return freqs_cis
# 旋转位置编码计算
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
# xq.shape = [batch_size, seq_len, dim]
# xq_.shape = [batch_size, seq_len, dim // 2, 2]
xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2)
xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2)
# 转为复数域
xq_ = torch.view_as_complex(xq_)
xk_ = torch.view_as_complex(xk_)
# 应用旋转操作,然后将结果转回实数域
# xq_out.shape = [batch_size, seq_len, dim]
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2)
return xq_out.type_as(xq), xk_out.type_as(xk)
class Attention(nn.Module):
def __init__(self, args: ModelArgs):
super().__init__()
self.wq = Linear(...)
self.wk = Linear(...)
self.wv = Linear(...)
self.freqs_cis = precompute_freqs_cis(dim, max_seq_len * 2)
def forward(self, x: torch.Tensor):
bsz, seqlen, _ = x.shape
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(batch_size, seq_len, dim)
xk = xk.view(batch_size, seq_len, dim)
xv = xv.view(batch_size, seq_len, dim)
# attention 操作之前,应用旋转位置编码
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
# scores.shape = (bs, seqlen, seqlen)
scores = torch.matmul(xq, xk.transpose(1, 2)) / math.sqrt(dim)
scores = F.softmax(scores.float(), dim=-1)
output = torch.matmul(scores, xv) # (batch_size, seq_len, dim)
# ......
In [239]: freqs_cis
Out[239]:
tensor([[ 1.0000+0.0000j, 1.0000+0.0000j, 1.0000+0.0000j, 1.0000+0.0000j],
[ 0.5403+0.8415j, 0.9950+0.0998j, 0.9999+0.0100j, 1.0000+0.0010j],
[-0.4161+0.9093j, 0.9801+0.1987j, 0.9998+0.0200j, 1.0000+0.0020j]])
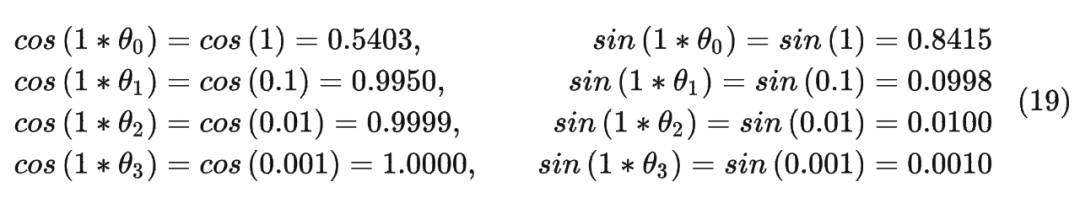
In [351]: q_ = q.float().reshape(*q.shape[:-1], -1, 2)
In [352]: q_[0]
Out[352]:
tensor([[[ 1.0247, 0.4782],
[ 1.5593, 0.2119],
[ 0.4175, 0.5309],
[ 0.4858, 0.1850]],
[[-1.7456, 0.6849],
[ 0.3844, 1.1492],
[ 0.1700, 0.2106],
[ 0.5433, 0.2261]],
[[-1.1206, 0.6969],
[ 0.8371, -0.7765],
[-0.3076, 0.1704],
[-0.5999, -1.7029]]])
In [353]: xq = torch.view_as_complex(q_)
In [354]: xq[0]
Out[354]:
tensor([[ 1.0247+0.4782j, 1.5593+0.2119j, 0.4175+0.5309j, 0.4858+0.1850j],
[-1.7456+0.6849j, 0.3844+1.1492j, 0.1700+0.2106j, 0.5433+0.2261j],
[-1.1206+0.6969j, 0.8371-0.7765j, -0.3076+0.1704j, -0.5999-1.7029j]])
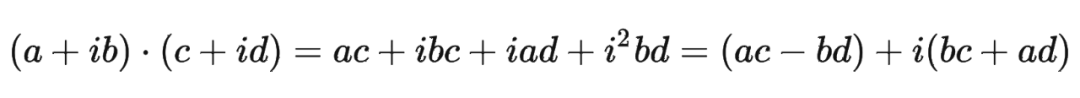
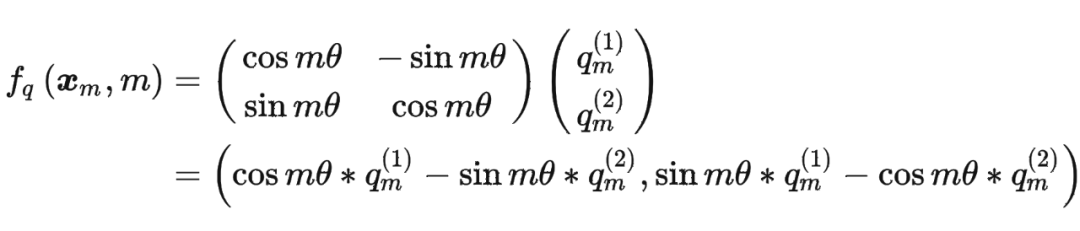
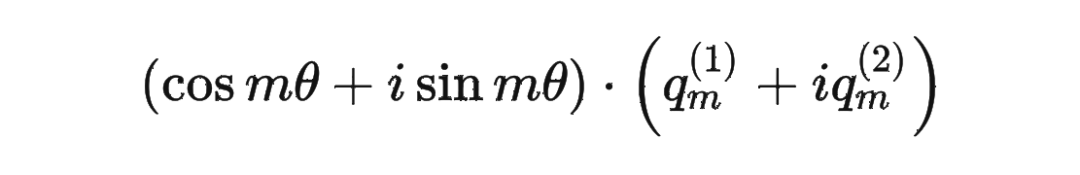
class RotaryEmbedding(torch.nn.Module):
def __init__(self, dim, base=10000, precision=torch.half, learnable=False):
super().__init__()
# 计算 \theta_i
inv_freq = 1. / (base ** (torch.arange(0, dim, 2).float() / dim))
inv_freq = inv_freq.half()
self.learnable = learnable
if learnable:
self.inv_freq = torch.nn.Parameter(inv_freq)
self.max_seq_len_cached = None
else:
self.register_buffer('inv_freq', inv_freq)
self.max_seq_len_cached = None
self.cos_cached = None
self.sin_cached = None
self.precision = precision
def forward(self, x, seq_dim=1, seq_len=None):
if seq_len is None:
seq_len = x.shape[seq_dim]
if self.max_seq_len_cached is None or (seq_len > self.max_seq_len_cached):
self.max_seq_len_cached = None if self.learnable else seq_len
# 生成 token 序列索引 t = [0, 1,..., seq_len-1]
t = torch.arange(seq_len, device=x.device, dtype=self.inv_freq.dtype)
# 对应m * \theta
freqs = torch.einsum('i,j->ij', t, self.inv_freq)
# 将 m * \theta 拼接两次,对应复数的实部和虚部
emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
if self.precision == torch.bfloat16:
emb = emb.float()
# [sx, 1 (b * np), hn]
cos_cached = emb.cos()[:, None, :] # 计算得到cos(m*\theta)
sin_cached = emb.sin()[:, None, :] # 计算得到cos(m*\theta)
if self.precision == torch.bfloat16:
cos_cached = cos_cached.bfloat16()
sin_cached = sin_cached.bfloat16()
if self.learnable:
return cos_cached, sin_cached
self.cos_cached, self.sin_cached = cos_cached, sin_cached
return self.cos_cached[:seq_len, ...], self.sin_cached[:seq_len, ...]
def _apply(self, fn):
if self.cos_cached is not None:
self.cos_cached = fn(self.cos_cached)
if self.sin_cached is not None:
self.sin_cached = fn(self.sin_cached)
return super()._apply(fn)
def rotate_half(x):
x1, x2 = x[..., :x.shape[-1] // 2], x[..., x.shape[-1] // 2:]
return torch.cat((-x2, x1), dim=x1.ndim - 1)

RoPE的外推性
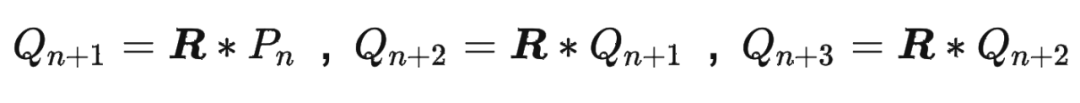
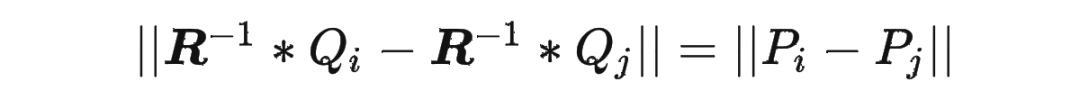

总结

附录
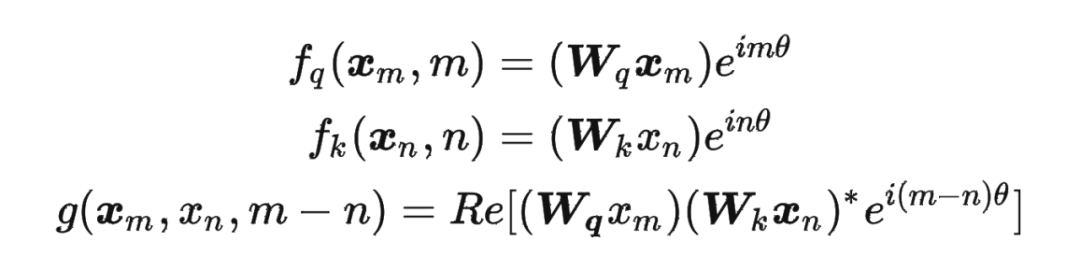
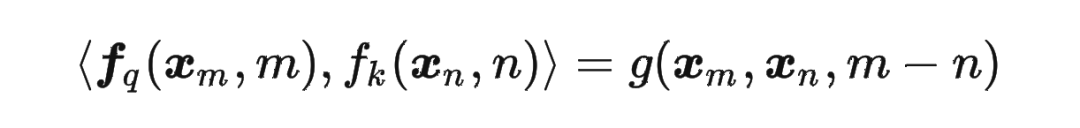
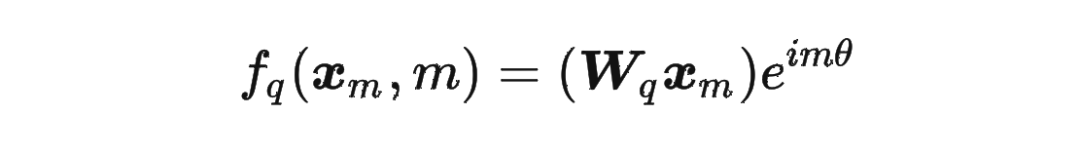
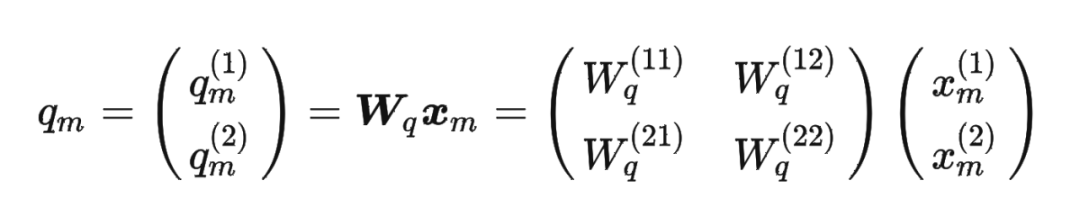
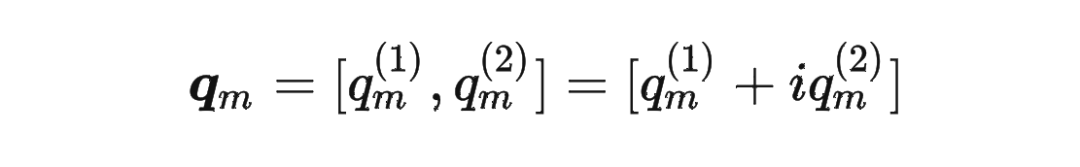
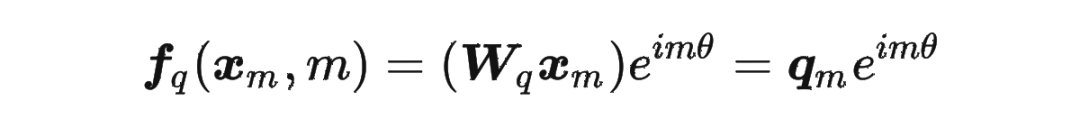
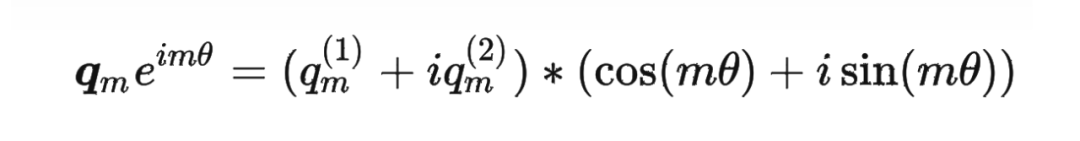
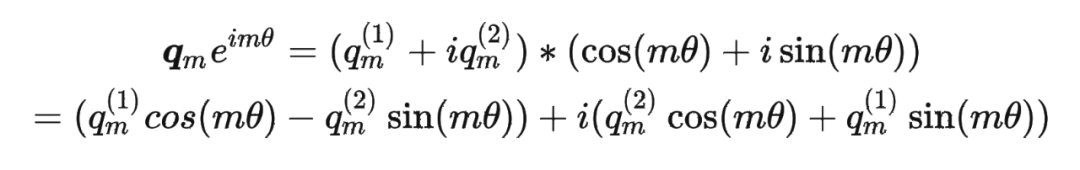
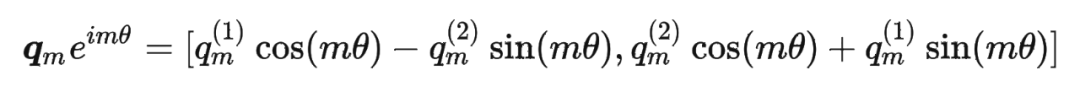
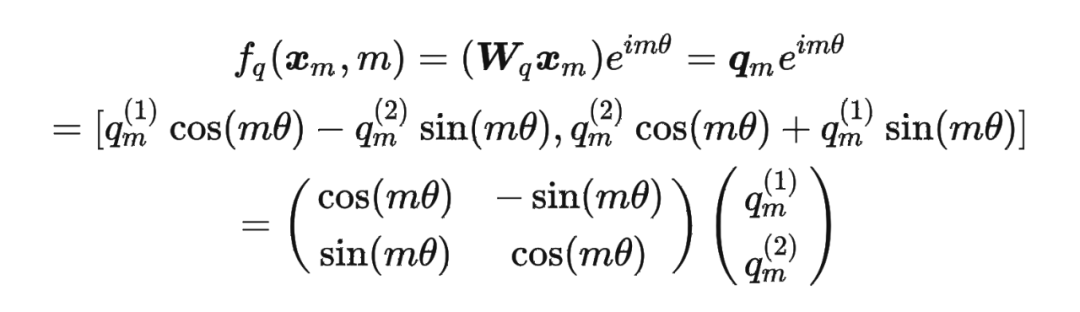
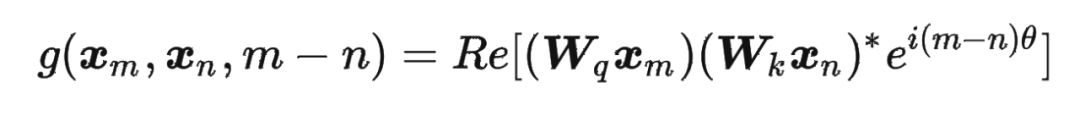
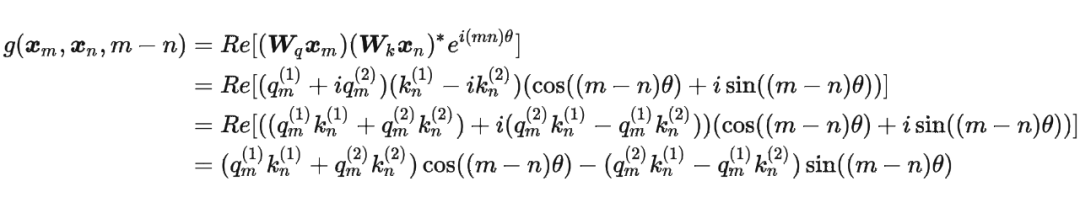
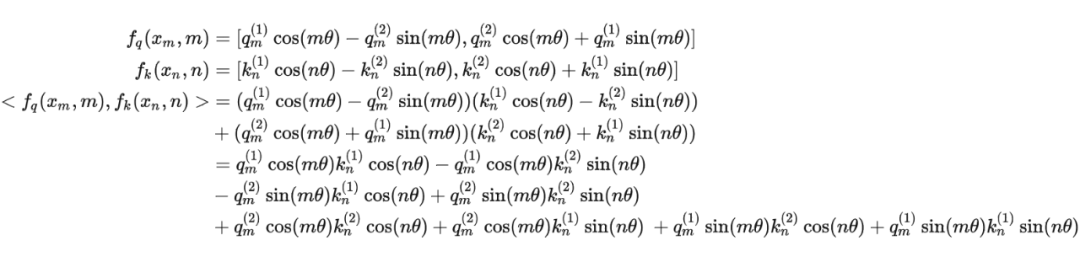
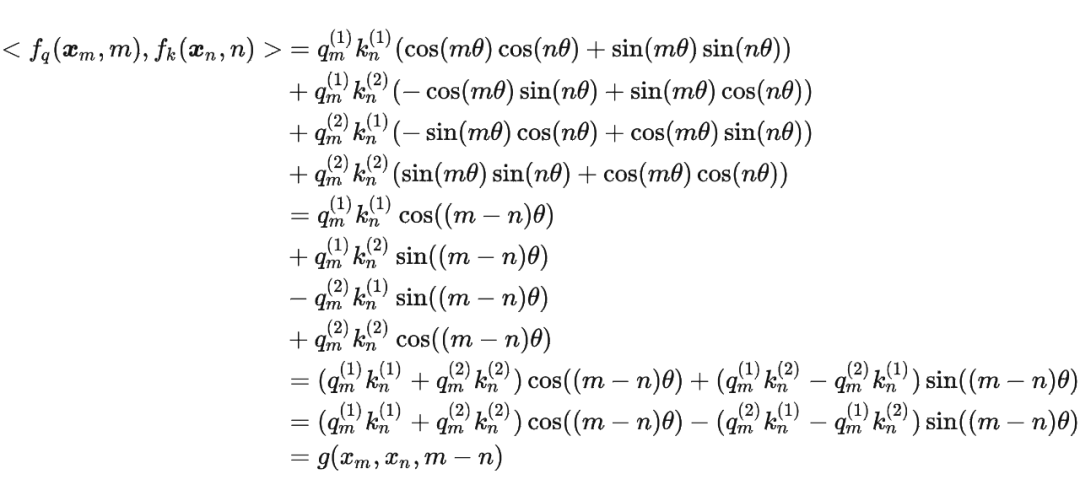
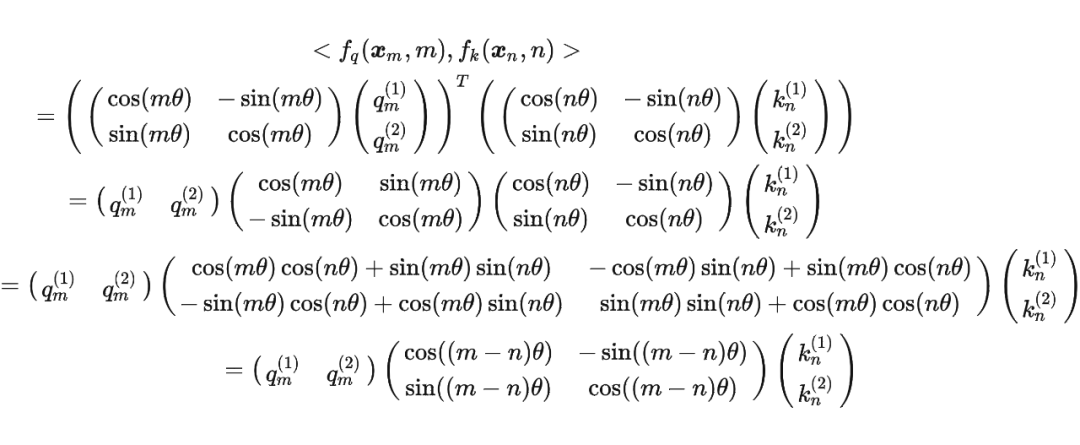
参考文献
[1] ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING https://arxiv.org/pdf/2104.09864.pdf
[2] 梁德澎:一文看懂 LLaMA 中的旋转式位置编码(Rotary Position Embedding)https://zhuanlan.zhihu.com/p/642884818
[3] 马梦之:一步一步,推导旋转位置编码(Rotary Position Embedding, RoPE)https://zhuanlan.zhihu.com/p/644585013
[4] Transformer升级之路:博采众长的旋转式位置编码
若觉得还不错的话,请点个 “赞” 或 “在看” 吧
全栈指导班
报名请扫描下方二维码,备注:“全栈班报名”

内容中包含的图片若涉及版权问题,请及时与我们联系删除




评论
沙发等你来抢