ti example 详解第 1 讲：Julia-set 分形绘制

在 Taichi 语言的官方示例 ti example 中积累了大量代码精炼，趣味性十足的 demo，但是由于没有配套解说，且 Taichi 语言本身也逐步加入了很多新功能新用法，使得很多想要学习借鉴的同学望而却步。此次文章计划准备挑选其中最具代表性的一些 demo 出来进行解说，并采用由简到难，逐步点亮 Taichi 技能树的教程形式展开，希望可以为社区中对 example 的实现原理感兴趣的同学提供参考。

ti-example 算例展示

本次文章计划将基于 Taichi 1.6.0 的版本，还没有安装 Taichi 的同学可以通过如下命令安装 Taichi：

$ pip install -U taichi

关于不同平台的安装问题，请先参考官方文档，仍有具体问题的，请关注文末的交流讨论群来和我们交流！

本系列文章此次将采用基于代码解说的方式，另一个目标是给大家提供一个和官方文档“自底向上”的风格截然不同的实战练级路径，不再拘泥于系统性地说明 Taichi 语言本身的语法，而是帮助读者理解代码中的实现原理以便后续根据自己的兴趣方向展开更多的实验开发。关于本次文章计划的选题，如果有特别希望解说的 example 可以在评论区留言，我们会根据社区需求安排在完成第一季的文章后进行不断补充。废话不多说，让我们进入本次的主题：第一个 example fractal.py 吧！

初次运行 Taichi 与 Taichi 的初始化

Taichi 是一门嵌入在 Python 中的高性能计算语言。说到“语言”，很多同学可能会先打个激灵：难道我为了加速计算又双叒要学一门新的语言了？别急，我们强调 Taichi 的语言属性更多的是因为其独立编译的属性，从用户的角度看，实际上 Taichi 的用法非常接近于大家熟悉的 Numpy，PyTorch 等 Python 库，使用时只需简单的 import 后调用相应接口即可。

安装 Taichi 以后我们可以在命令行中用如下命令来试玩 Taichi 的官方示例：

$ ti example

在随后的交互页面输入 example 编号即可运行。另外，如果需要将相应的 example 代码抓取到当前目录，可以利用 -s 选项，比如用如下命令就可以抓取到本次文章所用的示例代码了：

$ ti example -s fractal

在所有 Taichi 程序包括 fractal.py 代码中，我们需要先引入 Taichi 并将其初始化：

import taichi as ti
ti.init(arch=ti.gpu)

其中，ti.init() 中的 arch 参数告诉 Taichi 编译器应该将代码编译到何种后端。目前 Taichi 可用的后端已经非常丰富，其中 ti.cpu 代表在 CPU 上运行，ti.gpu 代表在 GPU 上运行，其中 GPU 包括多种后端包括 ti.cuda，ti.metal 等。

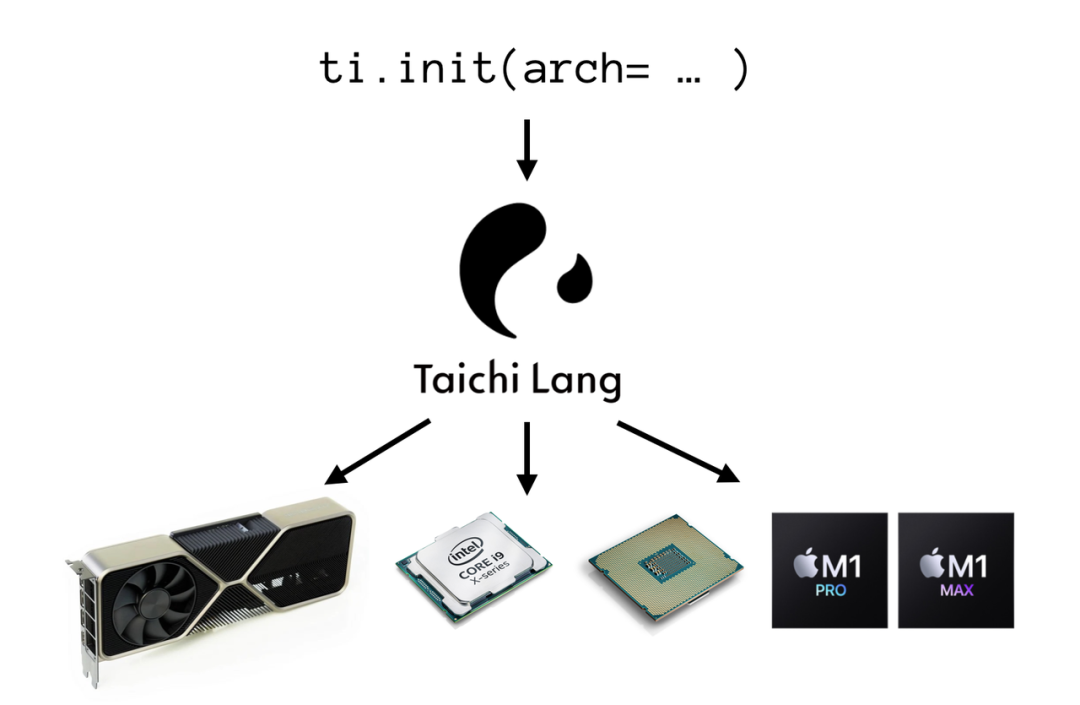
Taichi 多后端编译示意图

在了解了基本的安装与运行后，就让我们来看看用 Taichi 计算 Julia-set 分形的思路吧。

Julia 分形计算原理

fractal.py 的计算对象：Julia-set 是一种分形，而分形是一种特殊的几何形状，可以在不同的缩放层级上重复自身的模式。换句话说，当你放大或缩小分形的一部分时，你会看到与原始形状非常相似的结构。想象一下一个雪花的形状。如果你放大雪花的一个小部分，你会发现这个部分本身看起来也像一个雪花。这个特性在数学和自然界中都很常见。

Julia-set 的定义基于以下的一套规则：

1. 假设在 2D 复数平面上有一个点其坐标是
2. 对这个坐标进行这样一个迭代计算：，其中 为一个复数常数； 为复数的平方，假设 ，则
3. 如果在迭代 次以后 的模 依然在某个阈值范围以内，则认为该点 是分形内的点应该进行着色，反之则属于分形之外，不应该进行着色

举例来说，对于坐标原点 来说，由于其平方 也是 ，因此上述迭代的过程就可以简化为如下过程：

...

假设我们设置一个阈值为 20，以及最大迭代数 为 50，那么我们就可以在迭代计算 50 次以后通过比较 的模的大小得知该点是否应该着色。在下图中，我们尝试对空间中的两个点做上述的迭代运算，并观察各自的轨迹折线。可以看到，上图的起始点在迭代一定次数后其模就会开始发散，而下图的起始点则仍然收敛在一个较小的范围内：

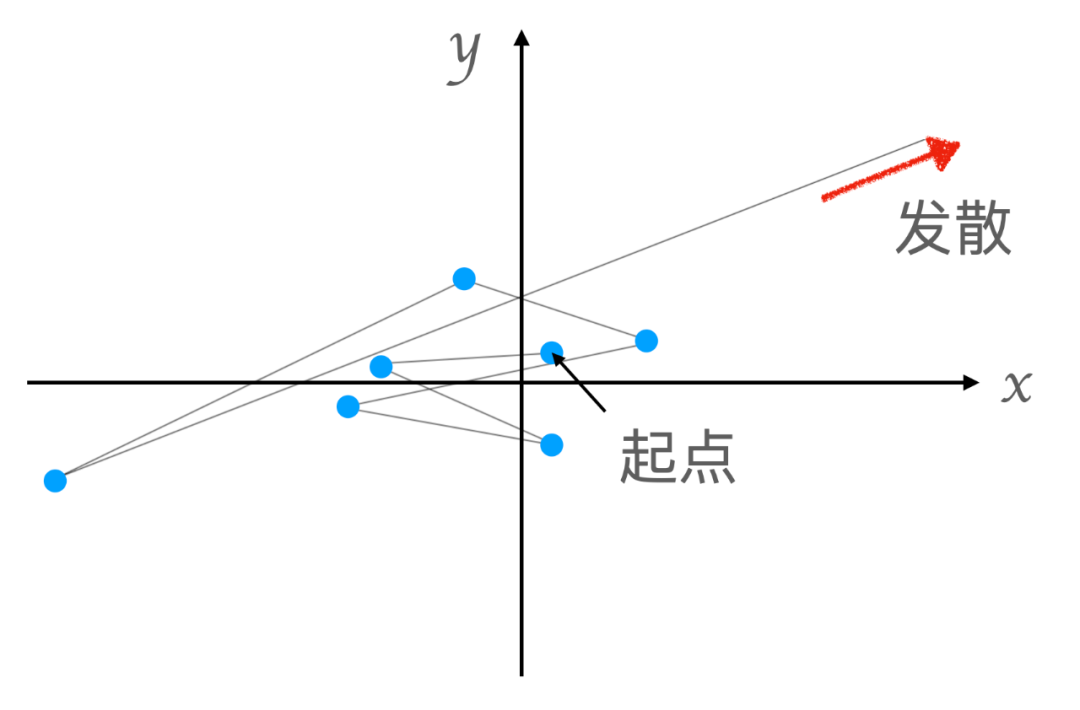
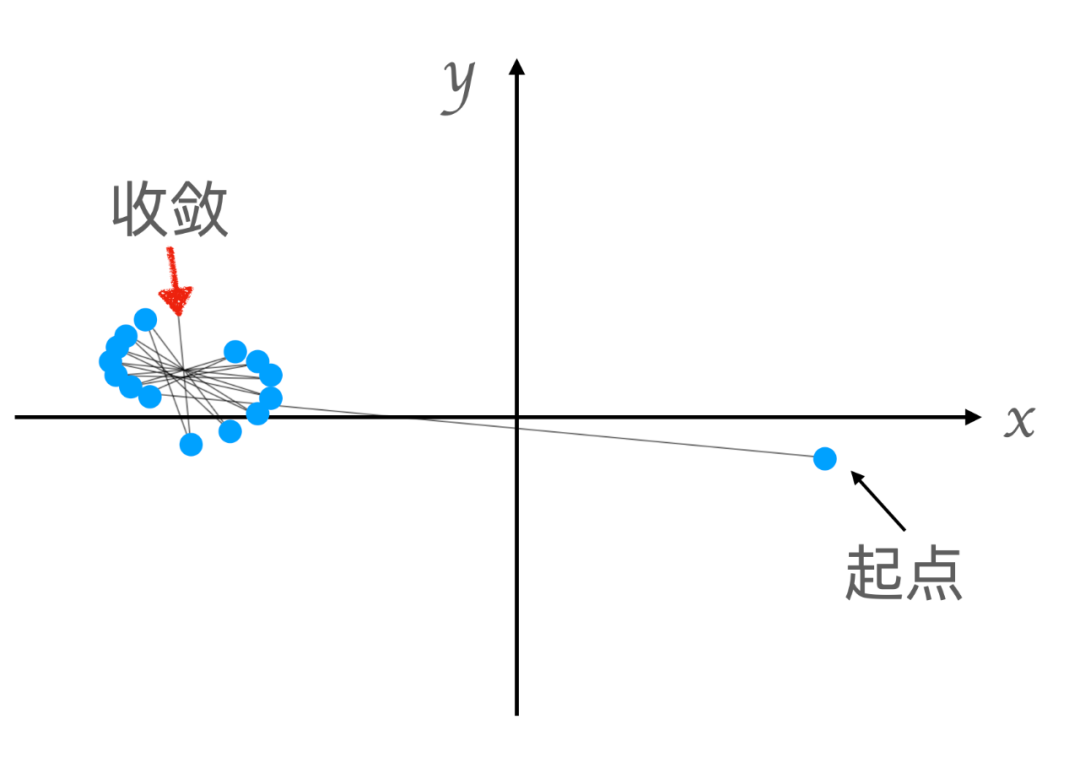
Julia-set 中点的轨迹示意

同理，我们对同一张画布上的所有坐标进行这样的迭代运算，就可以得知每个点的着色与否。理解了分形的计算原理，接下来我们就来看看如何在 Taichi 中进行这个计算吧。

Taichi 数据结构 ti.field 与核函数 ti.kernel

在任何编程语言中，数据结构和计算手段都是核心中的核心。在 Taichi 中，最基础和常用的数据结构是 ti.field，可以用来表达多维的标量，向量甚至自定义量。在 fractal.py 中，我们很直观的用一个 2 维的 ti.field 来表示画布上每一个点的灰度值：

n = 320
pixels = ti.field(dtype=float, shape=(n * 2, n))

其中 ti.filed 可以在参数中给定其数据类型 dtype 以及形状 shape ，其意义几乎是自明的因此我们不再赘述，具体的详细解释也可以参考官方文档。这里我们强调两点：

1. ti.field 的底层实现 SNodeTree 可以让我们很方便的调整其数据的内存排布，这也是 Taichi 区别于其他计算工具的重要特性之一；SNodeTree 在复杂情况下和连续内存排布的数组是不同的
2. Taichi 的自动并行功能以及核函数 kernel 也将围绕 ti.field 进行使用，两者相辅相成；Python 或者 Numpy 中的数据结构是不可以直接用 Taichi 的自动并行功能来遍历的

除了 ti.field Taichi 中也提供了更为单纯的，连续内存的数据容器：ti.ndarray ，其声明和访问方法和 ti.field 几乎一样，需要注意的是 kernel 如果需要访问 ti.ndarray 的值则需要在参数中注明其类型和维度。具体参见文档相关部分：https://docs.taichi-lang.org/docs/ndarray

有了存储灰度值的数据容器之后，我们就要根据上一节的算法来计算画布上的灰度值了。按照 Python 或者是 C/C++ 类语言的思路，遍历一个多维数组的写法大概是这样的：（下为示意代码，实际不可这样运行）

for i in range(n * 2):
    for j in range(n):
        pixel[i, j] = ...

这段代码的含义是按照先列后行的主序，对 pixel 中的元素进行一一逐次的顺序计算，并将计算结果存回 pixel 中。而在 Taichi 中，我们提出 kernel 以及自动并行的概念：我们注意到上述的 pixel 计算过程，每一个像素点的灰度值计算都是相互独立的，因此我们完全可以在多核 CPU/GPU 上并行地同时计算这些像素的值。在 fractal.py 中，我们使用了 Taichi 中提供的一种叫做 Struct-for 的 for 循环语法：

for i, j in pixel:
    pixel[i, j] = ...

这样的语法首先简化了多层 for 循环的表达，仅用一行就完成了多层嵌套循环的语义；不仅如此，在这个 for 循环中每个元素的计算还会被自动并行，由多个计算核心同时执行。关于 Taichi 中的各种 for 循环以及其细微差别，读者可以查询官方文档（https://docs.taichi-lang.org/docs/language_reference#the-for-statement）。

最后，我们还要告诉 Taichi 编译器，此部分并行计算代码希望通过 Taichi 编译器编译并部署到多核心设备上，为此我们只需给这部分函数加上一个特定的修饰符 @ti.kernel 即可：

@ti.kernel
def paint(t: float):
    for i, j in pixels:  # Parallelized over all pixels
        ...

注意到这里的 paint 参数中，我们显式地指定了其数据类型为 float ，这在 kernel 中是一个必须的要求，Taichi 需要根据这些数据类型对 kernel 代码进行编译，我们不能像在 Python 中一样随意给参数代入任何类型，这也是 Taichi 调用时和 Python 的明显区别。本算例中还用到了另一个修饰符 @ti.func ，这是用来修饰被 kernel 调用的工具函数的符号。你可以将 ti.func 理解为给 ti.kernel 打工的小弟，通过使用 ti.func 我们可以对 kernel 中某些重复的运算比如 complex_sqr() 进行提炼，使代码更加精炼简洁。至此，我们已经可以读懂 fractal.py 中的大部分主要计算逻辑。

Kernel 可能对于不熟悉 GPU 计算的读者来说是一个比较陌生的名词，想要了解更多背景信息的读者可以自行查询 CUDA 中关于核函数 kernel 的背景知识。对于 Taichi 用户来说，我们可以将 kernel 简单理解为“对大规模数据进行并行处理的函数（function）”即可。

One last thing：ti.Vector 数据类型

在分形计算中，我们用到了 ti.Vector 来表示复数 和 ：

c = ti.Vector([-2, ti.cos(t) * 0.2])
z = ti.Vector([i / n - 1, j / n - 0.5]) * 2

ti.Vector 是 Taichi 中用于表示向量的数据类型。注意这里的“向量”指的是我们在物理或者数学中常见的例如空间位置，速度，应力等概念。不同于大型数据容器，ti.Vector 旨在表达需要频繁进行向量运算的小型多维向量，其定位和 ti.i32 ，ti.f32 等类似属于数据类型而不是容器。举例来说我们在数值计算中常见的求解线性系统时遇到的大规模方程组 中的 虽然在数学上也称为向量，但是由于其规模往往极大，因此在计算上不适合用 ti.Vector 来表示。

另外，在 Taichi 中还有一个和 ti.Vector 容易混淆的接口 ti.types.vector ，此为用于构造多维向量类型的“类型产生器”，比如我们可以用如下语句自定义一个 5 维向量类型 vec5f：

vec5f = ti.types.vector(5, float)

最后，必须指出 ti.Vector 不具有全局变量的属性，仅能在当前 scope 中提供暂时的方便运算。如果要将 ti.Vector 在 kernel 间进行计算以及传递，则必须将 ti.Vector 包装成 ti.field 或者 ndarray。

结果与总结

在完成对 pixel 中像素的遍历计算后，fractal.py 通过 ti.GUI 这个简单的内置可视化窗口将其显示在了屏幕上，也就是我们在 Taichi 官方仓库主页中喜闻乐见的如下动画：

fractal.py 最终运行效果

本期我们通过对第一个 example：fractal.py 的解说，学习了 Taichi 语言的安装和基本运行方法，并且初步尝试了使用 Taichi 提供的数据容器 ti.field 以及自动并行 for 循环功能去求解一个分形图形的问题。代码虽短，其实其中凝聚了很多对于代码构造的思考和分形图案的理解。下一期我们将在此基础之上，通过一个经典却简洁的物理仿真问题：Nbody 多体模拟来向大家展示如何基于 Taichi 进行基础的物理仿真。

编辑心语

著名物理学家费曼说过："What I cannot create, I do not understand."。看过可能就会“知道”，但是只有动手做过才会真正“理解”。比如此次的主题 fractal.py 其实在如何呈现最终效果上巧妙地使用了时间 t 并对画布进行了有层次的绘制，你能自己动手试一试进一步创造出不同的动画效果吗？