点关注,不迷路,用心整理每一篇算法干货~
本文为时序领域新SOTA。它以时序多周期性为出发点,将复杂的时间变化分解为多个周期内和周期间的变化,将一维时间序列转换为一组基于多个周期的二维张量,应用二维卷积核建模,提取复杂的时间变化,显著提升了TimesNet在五种主流时间序列分析任务(短期和长期预测、填补、分类和异常检测)的表现。推荐阅读指数:5星。不足之处,还望批评指正。
论文:ICLR2023 | Timesnet: Temporal 2d-variation modeling for general time series analysis [1]
作者:Wu, Haixu, Tengge Hu, Yong Liu, Hang Zhou, Jianmin Wang, and Mingsheng Long
机构:清华
代码:https://github.com/thuml/TimesNet
引用量:29

本文以时序多周期性为出发点,将复杂的时间变化分解为多个周期内和周期间的变化,将一维时间序列转换为一组基于多个周期的二维张量,应用二维卷积核建模,提取复杂的时间变化,显著提升了TimesNet在五种主流时间序列分析任务(短期和长期预测、填补、分类和异常检测)的表现。
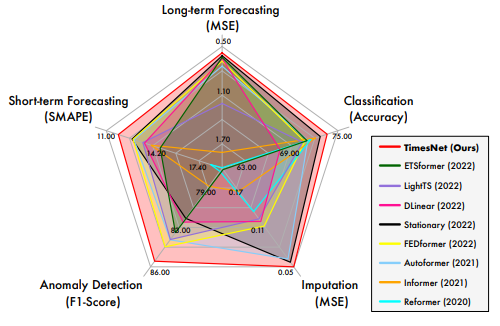
雷达图的来源是不同模型在不同任务下的得分排名(可自行见附录)
Q:怎么发现数据的多周期性?
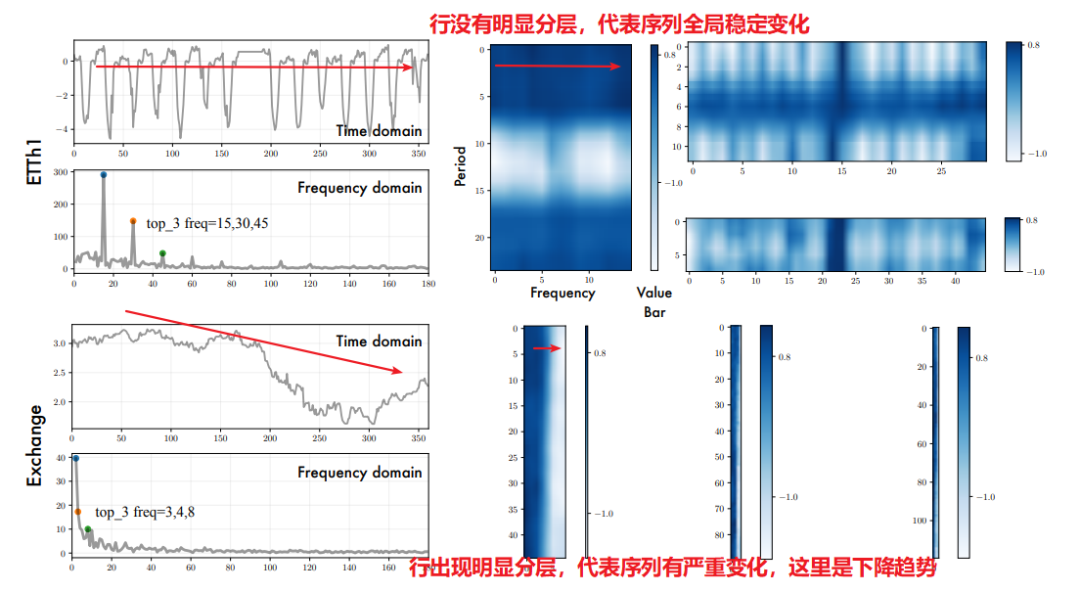
A:作者用FFT将原数据转为频谱,对每个长度为96的窗口序列选择出top 6明显频率。然后,收集对应的周期长度,并绘制其归一化密度图,如下图所示,便能看出多周期性。如Electricity,数据集包括长度12和24的周期。
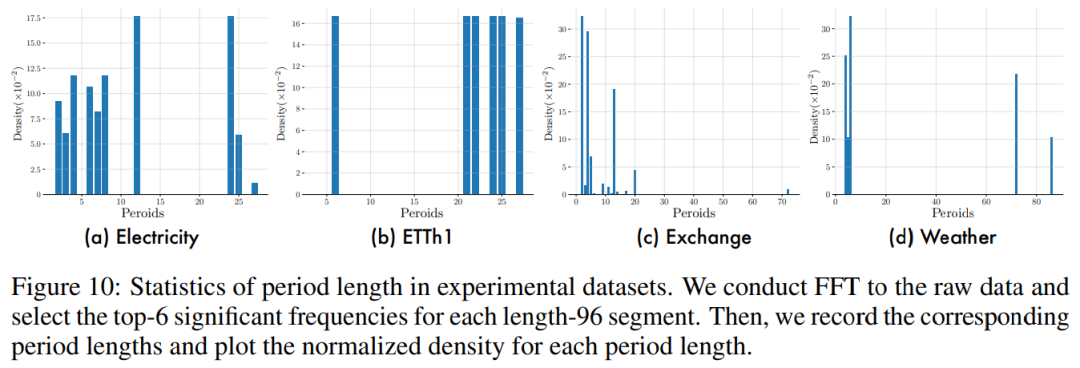
为了模型更好的从数据中捕捉多周期的变化,作者将时序多个周期抽取出来,按下图组织数据:

其中,红色为周期内变化(类似环比的概念,昨天跟今天的变化),蓝色为周期间变化(类似同比的概念,上周一和这周一的变化)。这样我们在2D数据上做卷积操作,再融合多周期下的结果,不就能捕捉到多周期的时序变化了吗?如下图所示:
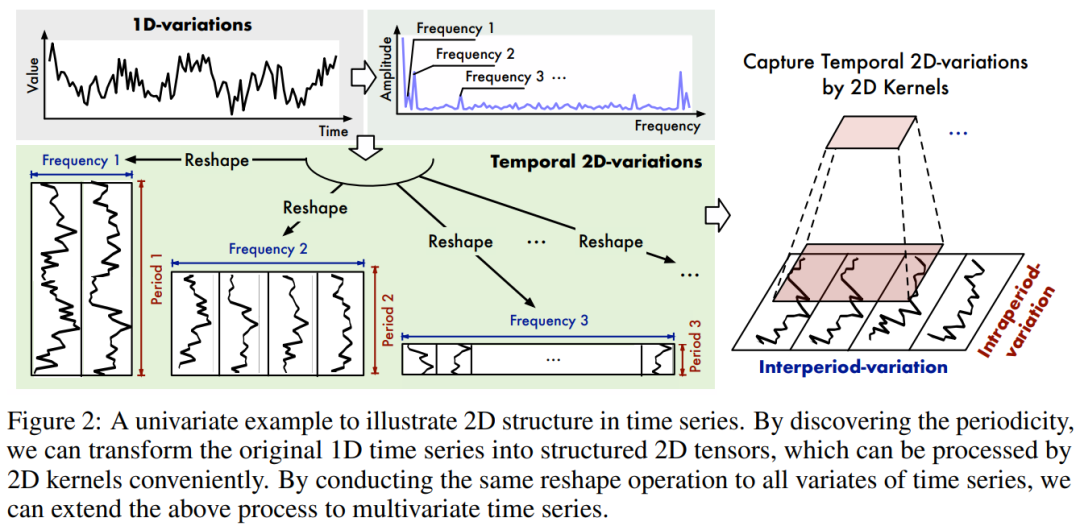
为此,作者提出了TimesNet,其里面最重要的是TimesBlock模块。该模块做了以下工作:
- 将1D时序转为2D结构数据;
- 2D卷积核捕捉信息;
- 动态合并多周期。
Q:首先,那如何将1D时序转为2D结构数据?
A:先用FFT得到频域,然后计算每个频率的振幅,A_j代表频率j的振幅。选择振幅最高的topk个频率,最后T/j得到对应频率的周期长度。

代码如下:
def FFT_for_Period(x, k=2):# [B, T, C]# [32,192,16] -> [32,97,16]# 使用快速傅里叶变换,得到T/2+1个频率xf = torch.fft.rfft(x, dim=1)# find period by amplitudes# 在样本维度上求均值,得到所有样本的平均振幅# 在通道维度上求均值,得到所有特征的平均振幅# 得到的频率列表维度为 [T/2+1]frequency_list = abs(xf).mean(0).mean(-1)# 频率列表首位元素为直流分量,值较大,为避免影响后续topk选取,置为0# ref: https://github.com/thuml/Time-Series-Library/issues/7frequency_list[0] = 0# 从频率列表中选择振幅最高的k个元素 [k]# 返回两个张量,第一个是未使用的排序结果,第二个是topk的索引_, top_list = torch.topk(frequency_list, k)# 计算实际周期,即时间步数除以top_list中每个频率对应的索引值(周期长度)# 得到的结果维度为[32, k]top_list = top_list.detach().cpu().numpy()period = x.shape[1] // top_list # [k]# 返回实际周期和振幅# 振幅通过在最后一维上求均值得到每个频率的平均振幅 [B, k]return period, abs(xf).mean(-1)[:, top_list]
之后,就是按照不同周期长度,对数据截取堆叠成2D。由于可能出现输入序列的时间长度不能被给定的周期长度整除,所以需要做0值填补,保证1D转化成2D能顺利完成。
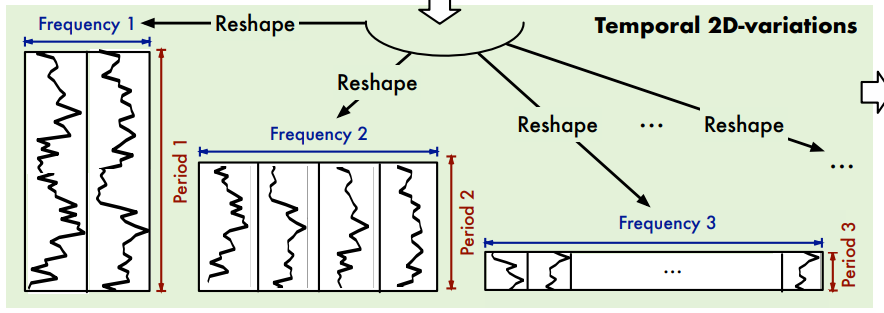
代码如下:
def forward(self, x):B, T, N = x.size()# period_list: 各top振幅频率j的周期长度,维度[k]# period_weight: 各样本下,各top振幅频率j的平均振幅,维度[B, k]period_list, period_weight = FFT_for_Period(x, self.k)res = []for i in range(self.k):# 获取第i个频率对应的周期长度period = period_list[i]# padding# 若周期过大,超过数据范围则需要padding# 为什么数据范围要考虑pred_len?# 因为对于预测任务来说,TimesNet的pipeline是:# 在embedding之后先将序列长度扩充为self.seq_len + self.pred_len,然后再不# 断refine预测结果。所以在中间层的TimesBlock其实在处理预测的中间结果(其长度# 为self.seq_len + self.pred_len)。if (self.seq_len + self.pred_len) % period != 0:# 计算调整后的序列长度,使其能够整除周期长度length = (((self.seq_len + self.pred_len) // period) + 1) * period# 创建一个0填充张量,形状为 [B, 填充长度, N]padding = torch.zeros([x.shape[0], (length - (self.seq_len + self.pred_len)), x.shape[2]]).to(x.device)# 合并out = torch.cat([x, padding], dim=1)else:length = (self.seq_len + self.pred_len)out = x# reshape# 将输入张量进行形状变换和维度置换# 将长度为 length 的序列划分为 length//period 个长度为 period 的子序列# 将通道数特征放在第 2 维度上,将子序列放在第 3 维度上# 得到的结果维度为 [B, N, length//period, period]out = out.reshape(B, length // period, period,N).permute(0, 3, 1, 2).contiguous()# 2D conv: from 1d Variation to 2d Variationout = self.conv(out)# reshape backout = out.permute(0, 2, 3, 1).reshape(B, -1, N)res.append(out[:, :(self.seq_len + self.pred_len), :]) # 保留前seq_len+pred_len长度的T,后面padding部分丢弃res = torch.stack(res, dim=-1)# adaptive aggregation# 基于每个A,softmax算权重period_weight = F.softmax(period_weight, dim=1)period_weight = period_weight.unsqueeze(1).unsqueeze(1).repeat(1, T, N, 1)# 加权融合res = torch.sum(res * period_weight, -1)# residual connectionres = res + xreturn res
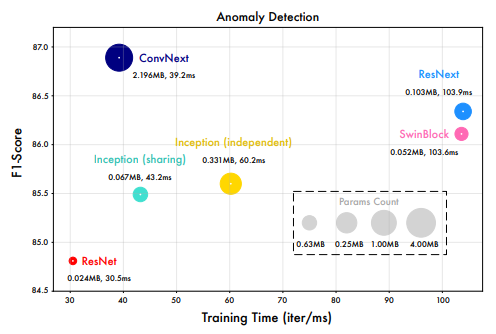
若看完上面的代码,你也便知道TimesBlock后续在2D数据上是如何做“2D卷积核捕捉信息”和“动态合并多周期”了。简单来说,作者是用了Inception去2D卷积捕捉信息。你也可以用其它CV的骨干网络替换,如下图所示。
# parameter-efficient designself.conv = nn.Sequential(Inception_Block_V1(configs.d_model, configs.d_ff,num_kernels=configs.num_kernels),nn.GELU(),Inception_Block_V1(configs.d_ff, configs.d_model,num_kernels=configs.num_kernels))
确实能学到东西,有关注重点:
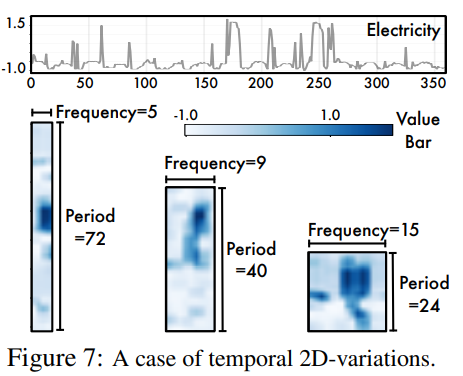
而动态合并多周期是:基于频率振幅算softmax权重,加权求和合并多周期下的卷积结果。作者也尝试过其它合并方式,比如直接求和和直接用振幅加权求和,效果都没有振幅+softmax+加权求和好。
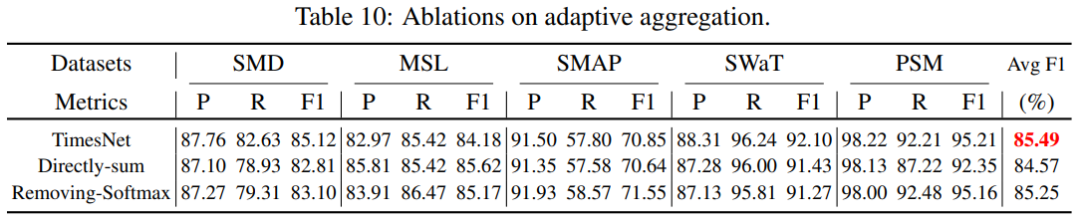
以上就是TimesBlock的完整内容,而TimesNet就是残差连接一连串TimesBlock。如下图所示,这里不做赘述:
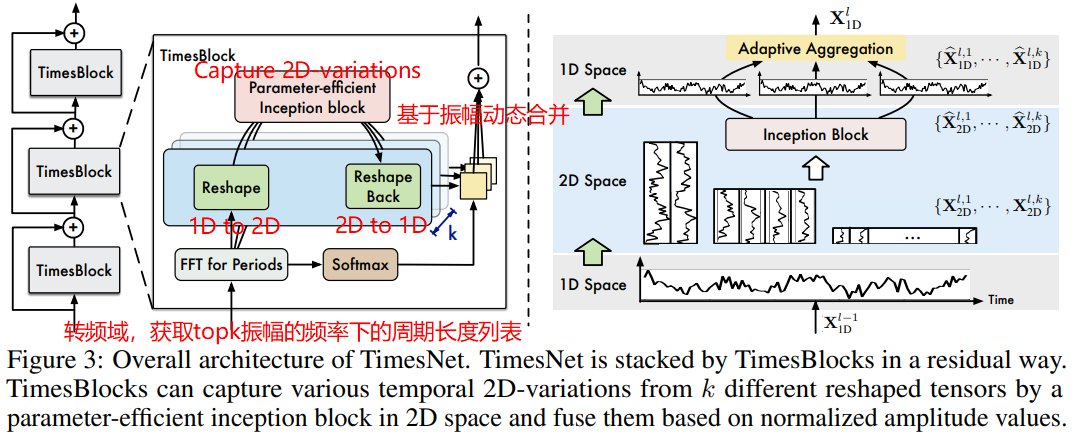
数据维度变换过程公式如下:
作者将TimesNet放到他们自研的Time-Series-Library库中,代码不长,思路也挺直戳要点的。感兴趣的朋友可以自行阅读代码,加深理解。在数据正式进入TimesNet中,有数据预处理:
- 参考他们之前发的Non-stationary Transformer做标准化;
- 做embedding:token embedding + position embedding + temporal embedding。然后再喂入线性层。需要注意,embedding输出,在时间维度上是:seq_len+pred_len。原因作者在Github有回复[2]:“对于预测任务来说,TimesNet的pipeline是:在embedding之后先将序列长度扩充为self.seq_len + self.pred_len,然后再不断refine预测结果。所以在中间层的TimesBlock其实在处理预测的中间结果(其长度为self.seq_len + self.pred_len)。”
def forecast(self, x_enc, x_mark_enc, x_dec, x_mark_dec):# encoder输入 x_enc: (batch_size, seq_len, enc_in)# encoder时间戳特征 x_mark_enc: (batch_size, seq_len, ts_fnum)# decoder输入 x_dec: (batch_size, label_len+pred_len, dec_out)# decoder时间戳特征 x_mark_dec: (batch_size, label_len+pred_len, ts_fnum)# Normalization from Non-stationary Transformer# 窗口标准化means = x_enc.mean(1, keepdim=True).detach()x_enc = x_enc - meansstdev = torch.sqrt(torch.var(x_enc, dim=1, keepdim=True, unbiased=False) + 1e-5)x_enc /= stdev# embedding:token embedding + postion embedding + temporal embedding。enc_out = self.enc_embedding(x_enc, x_mark_enc) # [B,T,d_model]# 用MLP在时间维度上,获取未来预测部分的序列。即[B,T,C]->[B,T+pred_len,d_model]enc_out = self.predict_linear(enc_out.permute(0, 2, 1)).permute(0, 2, 1) # align temporal dimension# TimesNet# 经过多少个TimeBlock# TimeBlock -> layer_norm -> TimeBlock -> layer_normfor i in range(self.layer):enc_out = self.layer_norm(self.model[i](enc_out))# porject back 输出预测序列 [B,pred_len,dec_out]dec_out = self.projection(enc_out)# De-Normalization from Non-stationary Transformer# 逆窗口标准化dec_out = dec_out * \(stdev[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1))dec_out = dec_out + \(means[:, 0, :].unsqueeze(1).repeat(1, self.pred_len + self.seq_len, 1))return dec_out
此外,每经过完一个TimesBlock,都会做一个Layer Normalization。无论是BN还是LN,两种Normalization都是为了让该层参数稳定,避免梯度消失或爆炸。具体区别如下:
- Batch Normalization: 对一批样本的每个特征做归一化,保留不同样本间的大小关系,适用CV领域;
- Layer Normalizatiom: 对每个样本所有特征做归一化,保留一个样本内不同特征间的大小关系,使用NLP领域。
来看下实验吧!我这边就只展示长短期预测表现吧,论文算附录部分的实验内容实在太多了,建议自行阅读。
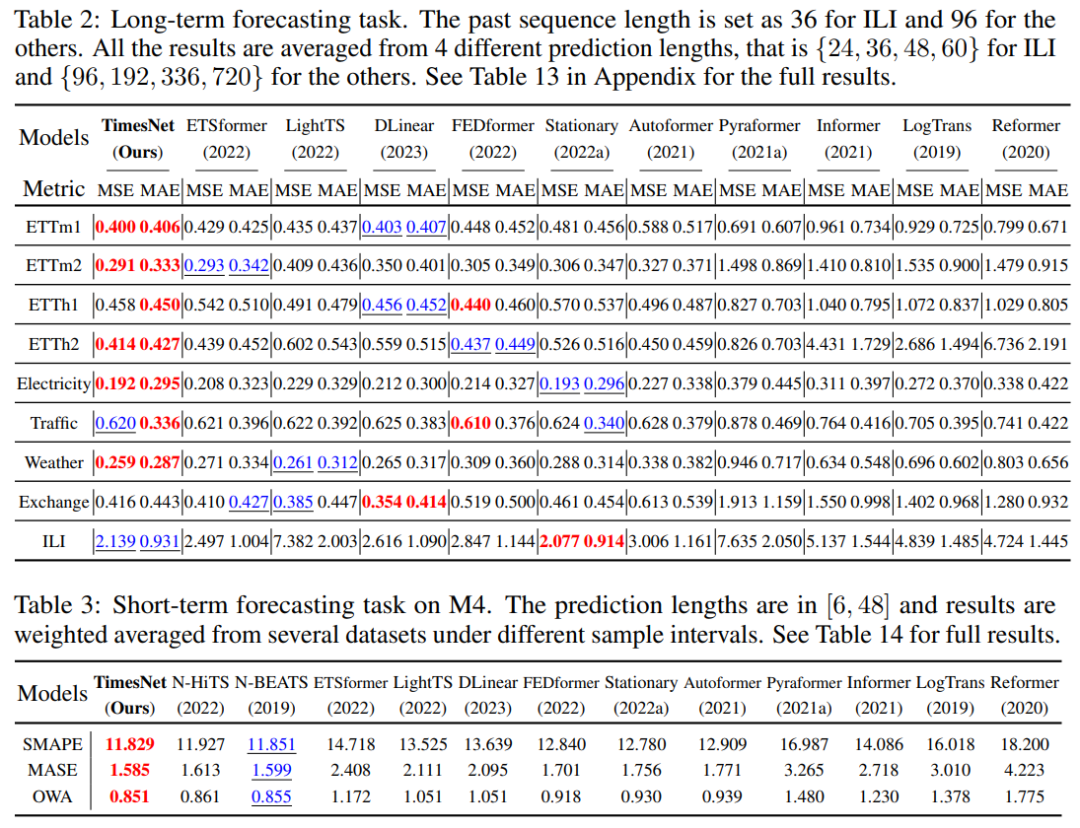
Q:FFT之后选择top k振幅的频率,k怎么定?
A:做实验调参,作者发现k=3适用时序填补、分类和异常检测任务。k=5适用于短期预测。
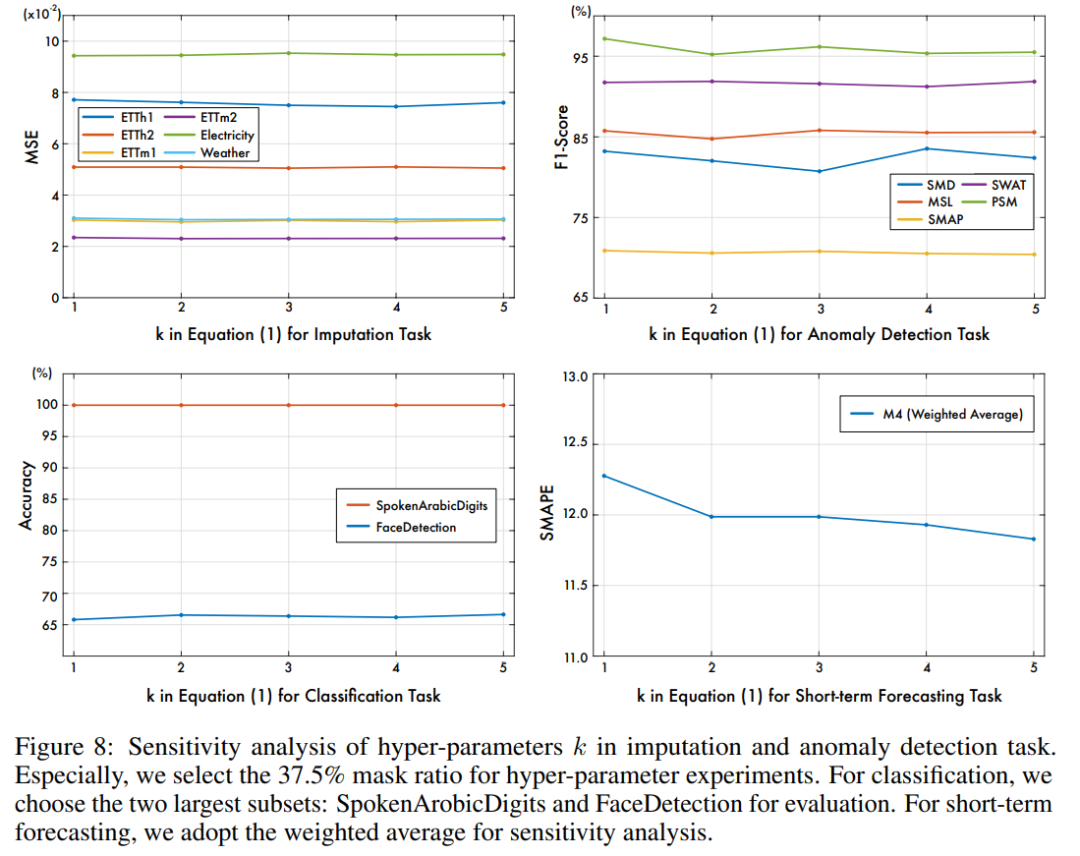
Q:d_model怎么定?
A:作者是根据不同任务,按公式配置不同d_model,可参考下面这表:
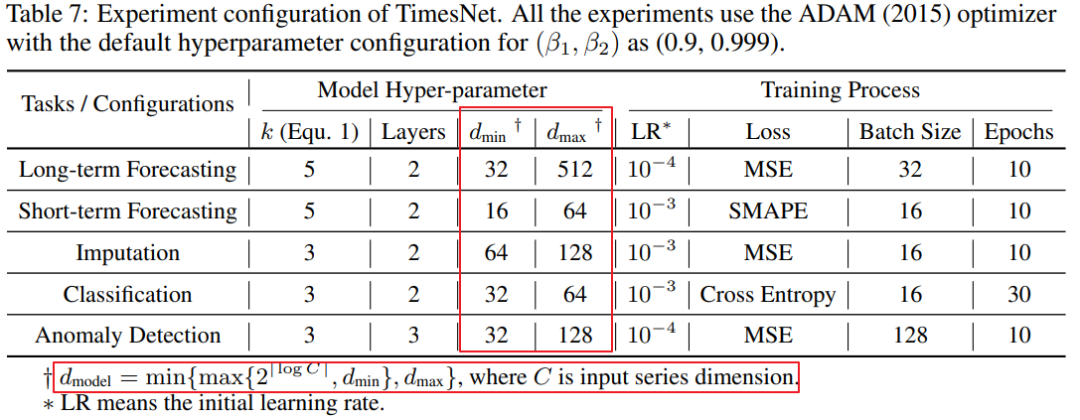
最后,总结全文,其实就是从时序数据可能存在多周期性,所以基于频域,将1D数据转化为2D后,应用2D卷积核,捕获2D周期间和周期内的时序变化,同时基于振幅,动态加权合并多周期的表征结果,给各大时序任务表现带来的明显的提升。

加交流群请加微信,备注机构+方向拉群~


内容中包含的图片若涉及版权问题,请及时与我们联系删除





评论
沙发等你来抢