✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
⛄ 内容介绍
随着科技的进步和股票市场的兴起,对股票开盘价的预测已成为投资者的迫切需要,而传统的预测方法无法准确预测股票开盘价的走势.因此,提出了一种基于长短期记忆神经网络的股票开盘价时间序列预测方法.首先,对获取的数据进行预处理,为后续的预测模型奠定了基础;其次,构建基于长短期记忆神经网络股票开盘价时间序列预测模型;最后,使用MATLAB进行仿真.与反向传播神经网络预测模型进行对比,长短期记忆神经网络模型的预测误差率仅为1.12%,预测精度提高了18.25%.仿真结果表明,长短期记忆神经网络对股票开盘价的预测较传统方法精度更高,为投资者对股票价格趋势发展提供了技术支撑.
LSTM(Long Short-Term Memory)是一种循环神经网络RNN)的变体,旨在解决传统RNN在处理长期依赖关系时出现的梯度消失和梯度爆炸问题。LSTM引入了一种记忆单元(memory cell)和门控机制(gate mechanism),以更好地捕捉和保持输入序列中的长期依赖信息。
LSTM的核心思想是通过三个门控单元(input gate、forget gate、output gate)来控制记忆单元中的信息流动,从而灵活地控制信息的存储和遗忘。下面是LSTM的基本原理:
输入门(Input Gate):输入门控制新的输入信息进入记忆单元。通过对输入数据和上一个时间步的隐藏状态进行操作,得到一个介于0和1之间的数值,表示是否接受新的输入。
遗忘门(Forget Gate):遗忘门控制何时遗忘之前的记忆。通过对输入数据和上一个时间步的隐藏状态进行操作,得到一个介于0和1之间的数值,表示是否保留之前的记忆。
记忆单元(Memory Cell):记忆单元负责存储和传递长期依赖信息。它根据输入门和遗忘门的控制,决定是否更新和保留记忆。
输出门(Output Gate):输出门控制从记忆单元输出的信息。通过对输入数据和上一个时间步的隐藏状态进行操作,得到一个介于0和1之间的数值,表示输出的权重。
LSTM的计算过程可以简单地概括为以下几个步骤:
输入数据和上一个时间步的隐藏状态通过输入门进行加权输入,得到候选记忆。
输入数据和上一个时间步的隐藏状态通过遗忘门进行加权输入,得到遗忘因子。
将候选记忆和遗忘因子相乘,得到更新后的记忆单元。
更新后的记忆单元通过输出门进行加权输出,得到当前时间步的隐藏状态。
LSTM网络通过以上的门控机制,可以有效地捕捉和保持长期依赖关系,避免梯度消失和梯度爆炸问题,从而提升模型在处理序列数据时的性能。
需要注意的是,LSTM网络可以根据具体问题进行扩展和修改,例如引入多层LSTM、双向LSTM等变体结构,以适应不同的应用需求。同时,LSTM也可以与其他神经网络结构相结合,构建更强大和复杂的深度学习模型。
⛄ 部分代码
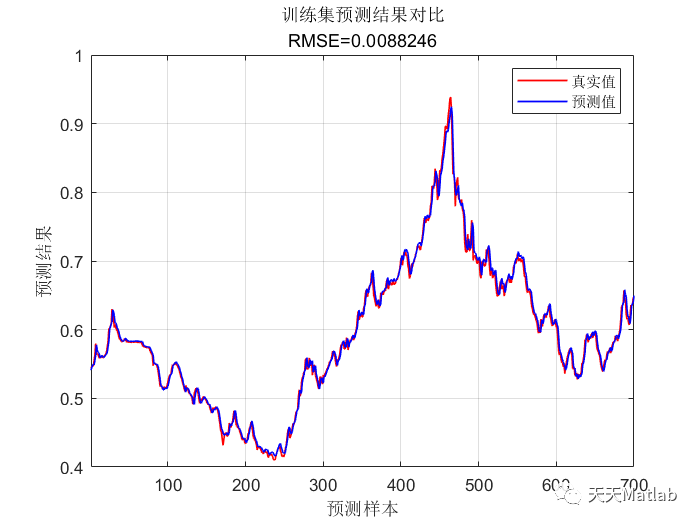
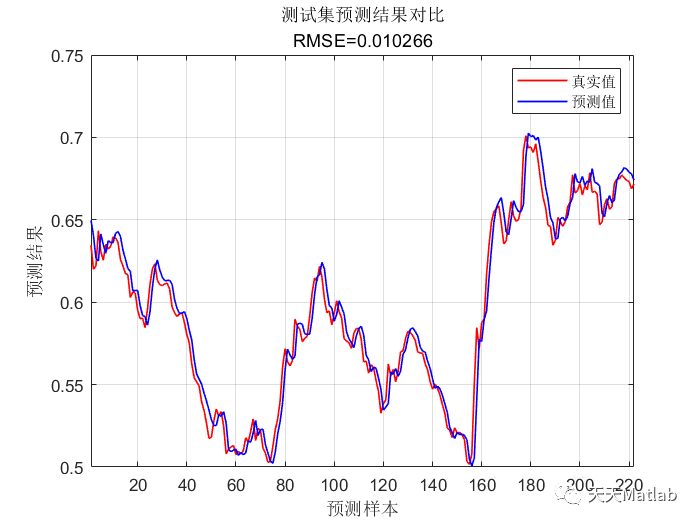
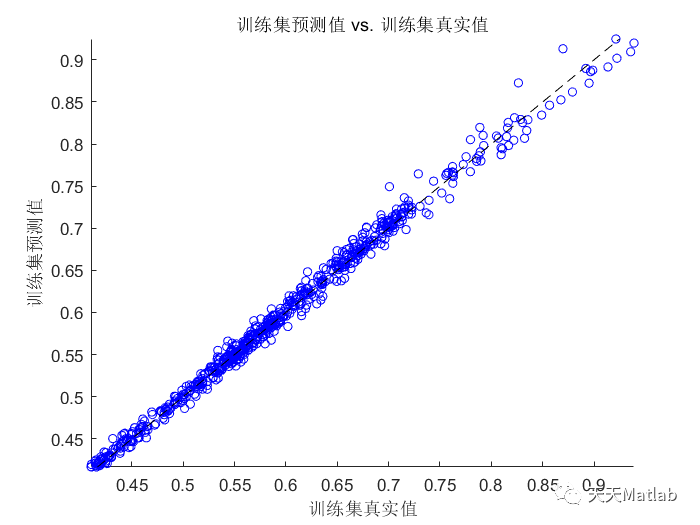
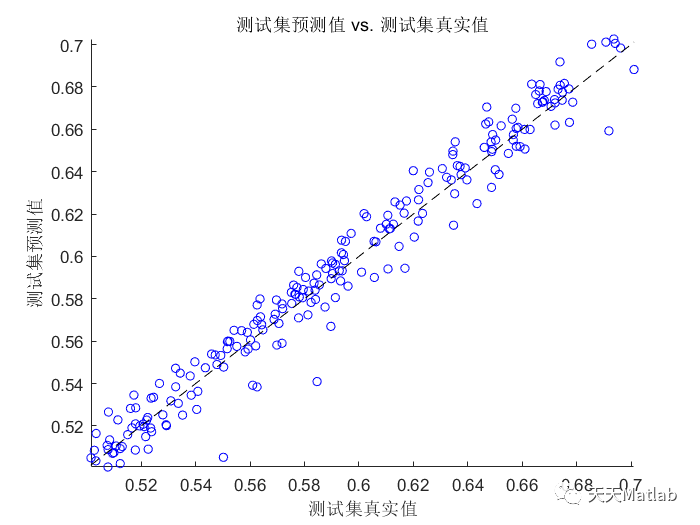
%% 清空环境变量warning off % 关闭报警信息close all % 关闭开启的图窗clear % 清空变量clc % 清空命令行%% 导入数据(时间序列的单列数据)result = xlsread('数据集.xlsx');%% 数据分析num_samples = length(result); % 样本个数kim = 15; % 延时步长(kim个历史数据作为自变量)zim = 1; % 跨zim个时间点进行预测%% 划分数据集for i = 1: num_samples - kim - zim + 1res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];end%% 划分训练集和测试集temp = 1: 1: 922;P_train = res(temp(1: 700), 1: 15)';T_train = res(temp(1: 700), 16)';M = size(P_train, 2);P_test = res(temp(701: end), 1: 15)';T_test = res(temp(701: end), 16)';N = size(P_test, 2);%% 数据归一化[P_train, ps_input] = mapminmax(P_train, 0, 1);P_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);t_test = mapminmax('apply', T_test, ps_output);%% 数据平铺% 将数据平铺成1维数据只是一种处理方式% 也可以平铺成2维数据,以及3维数据,需要修改对应模型结构% 但是应该始终和输入层数据结构保持一致P_train = double(reshape(P_train, 15, 1, 1, M));P_test = double(reshape(P_test , 15, 1, 1, N));t_train = t_train';t_test = t_test' ;%% 数据格式转换for i = 1 : Mp_train{i, 1} = P_train(:, :, 1, i);endfor i = 1 : Np_test{i, 1} = P_test( :, :, 1, i);end%% 创建模型layers = [sequenceInputLayer(15) % 建立输入层lstmLayer(10, 'OutputMode', 'last') % LSTM层reluLayer % Relu激活层fullyConnectedLayer(1) % 全连接层regressionLayer]; % 回归层%% 参数设置options = trainingOptions('adam', ... % Adam 梯度下降算法'MaxEpochs', 1200, ... % 最大训练次数'InitialLearnRate', 5e-3, ... % 初始学习率'LearnRateSchedule', 'piecewise', ... % 学习率下降'LearnRateDropFactor', 0.1, ... % 学习率下降因子'LearnRateDropPeriod', 800, ... % 经过 800 次训练后 学习率为 0.005 * 0.1'Shuffle', 'every-epoch', ... % 每次训练打乱数据集'Plots', 'training-progress', ... % 画出曲线'Verbose', false);%% 训练模型net = trainNetwork(p_train, t_train, layers, options);%% 仿真预测t_sim1 = predict(net, p_train);t_sim2 = predict(net, p_test );%% 数据反归一化T_sim1 = mapminmax('reverse', t_sim1, ps_output);T_sim2 = mapminmax('reverse', t_sim2, ps_output);%% 均方根误差error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);%% 查看网络结构analyzeNetwork(net)%% 绘图figureplot(1: M, T_train, 'r-', 1: M, T_sim1, 'b-', 'LineWidth', 1)legend('真实值', '预测值')xlabel('预测样本')ylabel('预测结果')string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};title(string)xlim([1, M])gridfigureplot(1: N, T_test, 'r-', 1: N, T_sim2, 'b-', 'LineWidth', 1)legend('真实值', '预测值')xlabel('预测样本')ylabel('预测结果')string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};title(string)xlim([1, N])grid%% 相关指标计算% R2R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;R2 = 1 - norm(T_test - T_sim2')^2 / norm(T_test - mean(T_test ))^2;disp(['训练集数据的R2为:', num2str(R1)])disp(['测试集数据的R2为:', num2str(R2)])% MAEmae1 = sum(abs(T_sim1' - T_train)) ./ M ;mae2 = sum(abs(T_sim2' - T_test )) ./ N ;disp(['训练集数据的MAE为:', num2str(mae1)])disp(['测试集数据的MAE为:', num2str(mae2)])% MBEmbe1 = sum(T_sim1' - T_train) ./ M ;mbe2 = sum(T_sim2' - T_test ) ./ N ;disp(['训练集数据的MBE为:', num2str(mbe1)])disp(['测试集数据的MBE为:', num2str(mbe2)])%% 绘制散点图sz = 25;c = 'b';figurescatter(T_train, T_sim1, sz, c)hold onplot(xlim, ylim, '--k')xlabel('训练集真实值');ylabel('训练集预测值');xlim([min(T_train) max(T_train)])ylim([min(T_sim1) max(T_sim1)])title('训练集预测值 vs. 训练集真实值')figurescatter(T_test, T_sim2, sz, c)hold onplot(xlim, ylim, '--k')xlabel('测试集真实值');ylabel('测试集预测值');xlim([min(T_test) max(T_test)])ylim([min(T_sim2) max(T_sim2)])title('测试集预测值 vs. 测试集真实值')⛄ 运行结果
⛄ 参考文献
[1] 徐一轩,伍卫国,王思敏,等.基于长短期记忆网络(LSTM)的数据中心温度预测算法[J].计算机技术与发展, 2019, 29(12):7.DOI:10.3969/j.issn.1673-629X.2019.12.001.
[2] 魏昱洲,许西宁.基于LSTM长短期记忆网络的超短期风速预测[J].电子测量与仪器学报, 2019(2):8.DOI:CNKI:SUN:DZIY.0.2019-02-008.
🍅 私信完整代码和数据获取及论文数模仿真定制
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络(CNN)、LSTM、支持向量机(SVM)、最小二乘支持向量机(LSSVM)、极限学习机(ELM)、核极限学习机(KELM)、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
2.图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
3 路径规划方面
旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
4 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配
、无人机安全通信轨迹在线优化
5 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
6 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
7 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
8 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长 火灾扩散
9 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合、状态估计
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢