新智元报道  

编辑：编辑部
【新智元导读】P/NP猜想是千禧年七大数学难题之一。如今，MSRA北大北航等机构华人团队，通过97轮「苏格拉底式推理」，让GPT-4得出结论P≠NP。

大语言模型，果然可以用来研究数学定理！
最近，微软亚洲研究院、北大、北航等机构的研究人员，通过97个回合的「苏格拉底式」严格推理，成功让GPT-4得出了「P≠NP」的结论！
论文地址：https://arxiv.org/abs/2309.05689
几个月前，数学天才陶哲轩曾在一篇博客中称，2026年，AI将与搜索和符号数学工具相结合，成为数学研究中值得信赖的合著者。
6月，加州理工、英伟达、MIT等机构的学者，就构建了一个基于开源LLM的定理证明器LeanDojo。
如今，GPT-4用出色的表现再次证明，LLM的确有进行科学研究和科学发现的能力。

P/NP难题有多难

作为美国克雷数学研究所（CMI）在2000年公布的七个千禧年难题之一，「P/NP问题」目前依然是理论信息学中计算复杂度理论领域里的未解之谜。
人们喜欢把它描述为「很可能是位居理论计算机科学核心的未解决问题」，也是人类提出的最深刻的问题之一。如果解决解决P/NP难题，将彻底改变人类文明进程。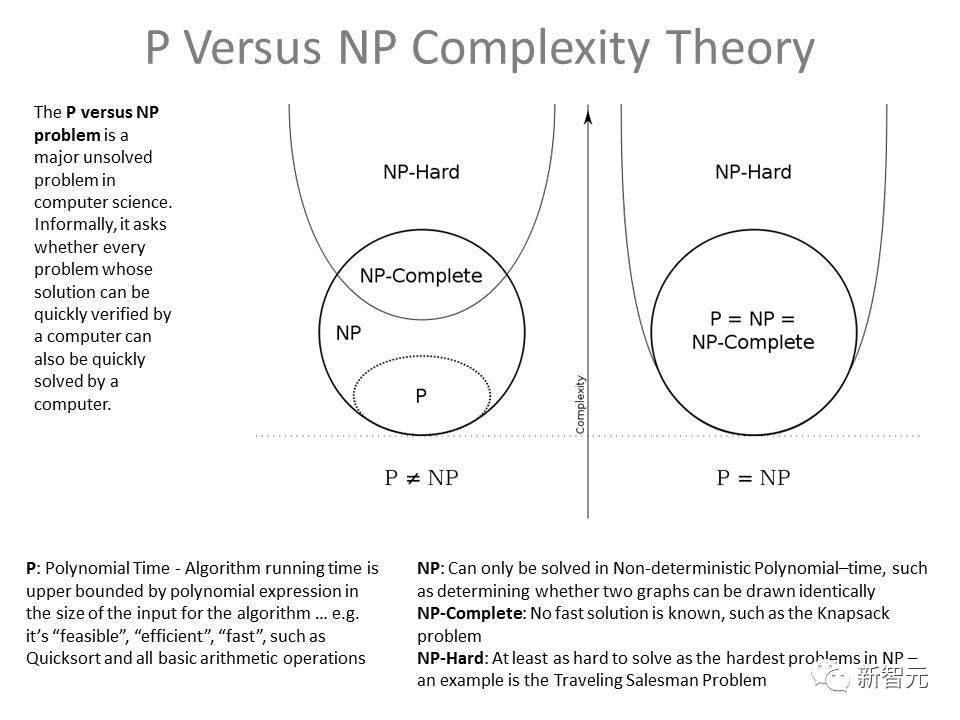
1971年，数学家Stephen A. Cook和Leonid Levin相对独立地提出这个问题：两个复杂度类P和NP是否是恒等的？
具体来说，一些永远无法通过简单计算得到答案的问题，就属于P/NP问题。
一个复杂问题如果能在多项式时间内解决，就被称为P问题，意味着计算机很容易将它求解。
那NP问题就是除了P问题之外的问题吗？未必。我们并不能证明一个问题能在多项式时间内解决，也无法证明它不能在多项式时间内解决。
所以，NP问题并不是非P类问题。
听起来似乎很复杂，我们可以用集水浒英雄卡的故事来类比。二十多年前集过卡的读者应该都知道，无论是加大购买量，还是扩大购买范围，都很难集齐全套水浒英雄。
这其实就是一个P/NP问题——是否有一种方法，让集卡的过程轻而易举？
所以，GPT-4是怎样得出P≠NP的？让我们往下看。

97轮对话，给出P≠NP结论

在这项研究中，研究者GPT-4学会了一种「苏格拉底式推理」。
他们引入了五个不同的角色（比如精通概率论的数学家），作为协助证明者，根据自己擅长证明不同的部分。
GPT-4用这种方法，开发了一种推理路径，得出了和北航Ke Xu、北工商Guangyan Zhou（论文三作和四作）最近提出结果一致的结论！
论文地址：https://arxiv.org/pdf/2302.09512.pdf
在最初的14轮对话中，GPT-4被引导设计出了初步的证明模式。
GPT-4被问的第一个问题是：「你能从哲学角度而不是计算机理论角度找到P!=NP问题背后的根本问题吗？」
在这个提示中，技巧在于鼓励模型创造性回答，避免进行检索。比如，「如何证明 P!=NP」这样的提示可能会引导大模型进行检索。
用上「苏格拉底式推理」中的转换模式后，就可以生成更具创新性的回答。
对于这个问题，GPT-4是这么回答的——
P!=NP问题背后的基本哲学问题，可以看作是创造力、直觉和洞察力（通常与NP问题相关）与系统化、算法和确定性方法（与P问题相关）之间的矛盾。
如果P=NP，那就意味着宇宙有一种基本的简单性，表面上看似复杂的问题都有高效、优雅的解决方案。
看来，GPT-4对P!=NP理解得很透彻，在此基础上，研究者开始提问了——
「 是否所有表面上看似复杂的问题都有高效、优雅的解决方案？如果不是，可以用什么方法来证明？」
GPT-4回答说，并非所有表面看来复杂的问题都有高效、优雅的解决方案，这可以归因于多种因素，比如所涉及变量的数量、变量之间关系的性质，或问题本身的内在难度。
然后，它提出了六种方法，其中一种是「矛盾证明」，即要证明一个问题没有高效、优雅的解决方案，可以假设存在这样的解决方案，然后证明这一假设会导致矛盾，这样就可以有力地证明某些解法不可能存在。
可以看到，GPT-4在回答问题过程中，真的像人类一样拥有思辨能力。
紧接着，研究人员趁热打铁，继续问道，「我们想用矛盾证明P!=NP，请列出几种可能的思路。」
这次GPT-4依然给出了六个答案，不过并不严谨。
要通过矛盾证明，必须找到一个无法在多项式时间内解决的NP完全（NP-complete）问题。
不过，这个回答可以启发GPT-4在以后的对话中思考NP完全问题。
在第四轮提问中，GPT-4的回答中出现了诸多亮点。

「该怎样构建这些问题呢？」
比如它回答说：我们可以从众所周知的NP完全问题入手，例如旅行商问题 （TSP）、布尔可满足性问题（SAT）或分团问题（Clique）。
随后的提问中，GPT-4被引导着给出了越来越多智慧的回答，也让研究开始一步步深入问题中心。

就这样，经过14轮连续对话，研究人员让GPT-4对3-13步的历史内容，梳理出一个证明思路。
对此，GPT-4的总结中，突出显示的两个部分是研究后续证明的2个关键点。
第4点建立了一个基本的直觉，即一旦证明了极难CSP的存在，就可以使用「矛盾证明」来证明这些问题无法在多项式时间内求解。
而第6点恰好成为后续证明工作的通用模式。
从下一轮开始，研究人员便遵循这一初步方案，严格地进行证明。
然后，研究者按照草稿，在随后的83轮对话中进行了严格的推理。
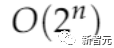而这97轮对话，可以说构建出了一个极难的NP完全问题，其中一些实例在时间复杂度低于（即穷举搜索）的情况下是不可解的，也就是说，证明结论为P≠NP。

是的，如果你能严格证明存在一种特定类型的NP完全问题，当变量数趋于无穷大时，无法在多项式时间内求解这类问题，就可以认为，证明了P!=NP。

在Ke Xu和Guangyan Zhou的论文中，他们构建了CSP和SAT的极难示例，证明了这些示例在没有穷举法的情况下无法求解。

而GPT-4，也得出了一致的结论。

是的，如果我们能够证明不存在一种算法能够以低于的时间复杂度解决某些SAT实例，那么当变量数量趋于无穷大时，它确实可以为某些无法在多项式时间内解决的NP完全问题的存在提供强有力的证据。

这项研究再次证明，GPT-4有充分的潜力与人类合作，共同探索极其复杂的专家级难题。
LLM不仅能掌握基本知识，还可以在广泛的解空间中发现新的见解。这也预示着科学LLM的范式下，科学发现的无限前景。

苏格拉底式推理

那么，GPT-4展现出如此强大，思维推理能力，背后的极致究竟是什么呢？
古希腊哲学家苏格拉曾说过，「我不能教会别人任何事，我只能让他们思考」。
这次，研究人员恰巧就从中汲取了灵感，提出一种通用问题的解决框架——苏格拉底式推理（Socratic Reasoning）。
简单讲，苏格拉底方法就是让我们「一步一步思考」，提出一系列问题激发批判性思维。
这对于大模型来说，如果能够进行批判性思考，就可以针对复杂问题提出高效的解决方案。
对此，研究团队指出这一框架旨在推动LLM解决高度复杂任务，协调各种子问题，并引导其搭建高层次推理途径。
「苏格拉底式推理」是在人类与LLM之间的一系列对话回合中进行的，是与LLM一起解决复杂挑战的递归机制。
如下图所示，「苏格拉底式推理」有5种强大的提示模式：演绎、转换、分解、验证、整合。
通过发掘新的见解和观点，将复杂问题分解为子问题或步骤，并通过质疑回答进行自我完善。

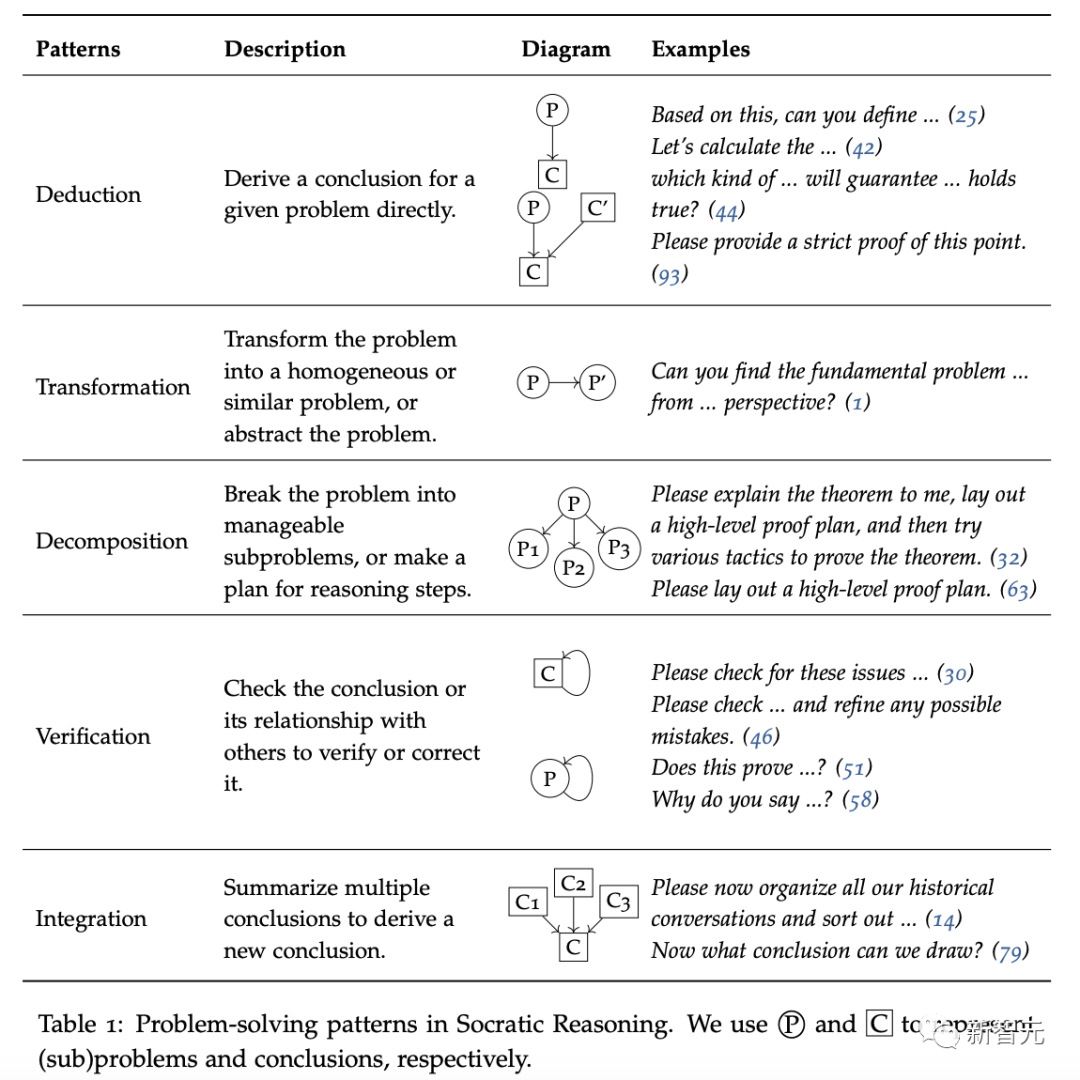
「苏格拉底式推理」中的问题解决模式（用和分别表示（子）问题和结论
一般来说，在处理可以直接从推理中得出结论的问题时，会采用「演绎模式」（如 「让我们一步步思考」）来指导LLM直接得出结论。
对于更复杂的问题，首先要求LLM将问题转化为新问题，或分解为若干子问题。然后，通过递归方法，直到找到「原子问题」。

P vs. NP问题对话转换示例

在生成新问题或得出新结论时，通过「验证模式」，利用LLM自我批判能力进行验证和完善。
最后，「整合模式」要求 LLM 基于子问题的结果合成结论。
整个流程，研究人员鼓励LLM通过一系列对话，递归地继续上述过程，直至解决目标问题。
这篇论文，研究人员揭示了大模型能够在解决科学问题中大有可为，能够在得出复杂问题结论中细化攻坚的策略。
通过97论文对话引导，GPT-4展现出超人能力，完成了千禧数学难题全推理过程。

作者介绍

Qingxiu Dong，北京大学计算语言学研究所博士生。
Li Dong，微软亚洲研究院首席研究员。
此前，他曾于2010年至2015年，在北航软件开发环境国家重点实验室跟随Ke Xu从事研究工作。
Ke Xu，北京航空航天大学计算机科学教授。
此前，他在北京航空航天大学获得了学士、硕士和博士学位。研究兴趣包括算法与复杂性、数据挖掘和网络。
参考资料：
https://arxiv.org/abs/2309.05689





内容中包含的图片若涉及版权问题，请及时与我们联系删除