点击下方卡片,关注「集智书童」公众号

随着检测器的快速发展,边界框回归(BBR)损失函数不断进行更新和优化。然而,现有的 IoU 基于 BBR 仍然集中在通过添加新损失项来加速收敛,忽略了 IoU 损失项本身的局限性。尽管从理论上讲,IoU 损失可以有效地描述边界框回归的状态,但在实际应用中,它无法根据不同的检测器和检测任务进行自适应调整,且不具备较强的泛化能力。
基于上述情况,作者首先分析了 BBR 模型,并得出结论:区分不同的回归样本以及使用不同尺度的辅助边界框计算损失可以有效加速边界框回归过程。对于高 IoU 样本,使用较小的辅助边界框计算损失可以加速收敛,而较大的辅助边界框适合于低 IoU 样本。然后,作者提出了 Inner-IoU 损失,通过辅助边界框计算 IoU 损失。对于不同的数据集和检测器,作者引入一个缩放因子比来控制计算损失的辅助边界框的尺度大小。最后,将 Inner-IoU 集成到现有的 IoU 基于损失函数中进行仿真和比较实验。
实验结果表明,利用本文提出的方法进一步提高了检测性能,验证了 Inner IoU 损失的有效性和泛化能力。
目标检测是计算机视觉中的基本任务,包括目标分类和定位。边界框回归损失函数是检测器定位分支的重要组成部分,检测器的定位精度在很大程度上取决于边界框回归,在当前的检测器中发挥着不可替代的作用。
在 BBR 中,IoU 损失可以准确描述预测边界框与 GT 框之间匹配的程度,确保模型在训练过程中可以学习到目标的位置信息。作为现有主流边界框回归损失函数的基本部分,IoU 定义如下:
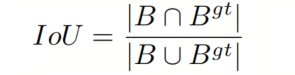
B 和 分别代表预测框和 GT 框。定义 IoU 之后,相应的损失可以定义如下:
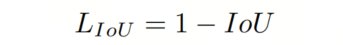
至今,基于 IoU 的损失函数逐渐成为主流并占据主导地位。大多数现有方法基于 IoU 并进一步添加新的损失项。例如,为了在Anchor框与 GT 框重叠区域为 0 时解决梯度消失问题,提出了 GIoU。GIoU定义如下,其中 C 是覆盖 B 和 的最小框:
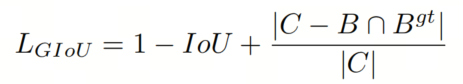
与 GIoU 相比,DIoU函数在 IoU 的基础上添加了一个新的距离损失项,主要通过最小化两个边界框中心点之间的归一化距离来达到更快收敛和更好的性能。它表示如下:
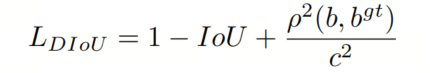
其中 b 和 分别是 B 和 的中心点,指的是欧氏距离, 是最小边界框的 diagonal。
CIoU进一步考虑了形状损失,并在 DIoU 损失的基础上添加了形状损失项。它表示如下:
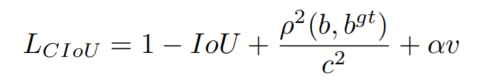
其中 是正交平衡参数:
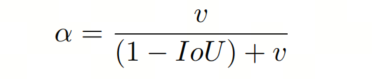
其中 衡量 aspect ratio 的一致性:
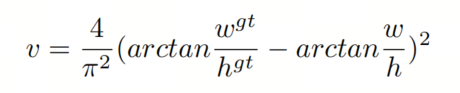
和 分别表示目标框的宽度和高度, 和 分别表示预测框的宽度和高度。当目标框和预测框的 aspect ratio 相同时,CIoU 将退化为 DIoU。
与 DIoU 相比,EIoU直接最小化目标框和Anchor框的宽度和高度以及中心位置的归一化差值。EIoU定义如下:
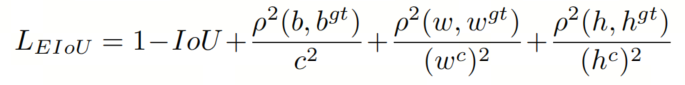
和 分别是覆盖目标框和预测框的最小边界框的宽度和高度。
最近的 SIoU 在考虑了Anchor框与 GT 框之间角度对边界框回归影响的基础上,将角度损失引入边界框回归损失函数。它定义如下:
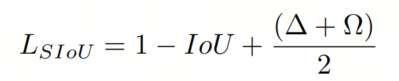
角度损失表示 GT 框和Anchor框中心点连接之间的最小角度:
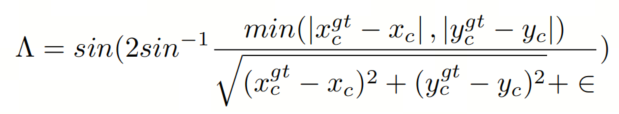
这一项旨在将Anchor框移动到最近的坐标轴,并根据角度变化优先考虑接近 X 轴或 Y 轴。当角度值为 45° 时,Λ = 1。当中心点沿 X 轴或 Y 轴对齐时,Λ = 0。
在考虑角度成本后,重新定义距离损失如下:
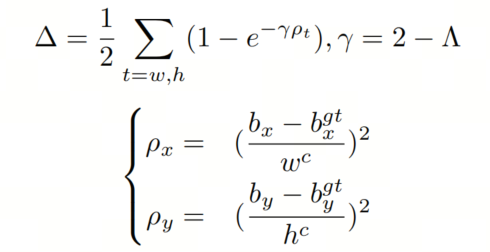
形状损失主要描述 GT 框和Anchor框之间的大小差异,定义如下:
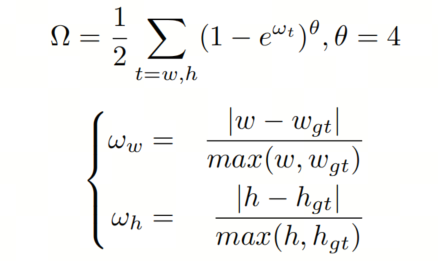
的值决定了形状成本的重要性。这个参数的范围从 2 到 6。
尽管上述边界框回归损失函数可以通过向 IoU 损失函数添加新的几何约束来加速收敛和改进检测性能,但它们并没有考虑 IoU 损失本身的合理性,这决定了检测结果的质量。为了弥补这一不足,作者提出了 Inner-IoU 损失,通过使用辅助边界框来加速回归,而无需添加任何新的损失项。
本文的主要贡献如下:
作者分析了边界框回归的过程和模式,并根据边界框回归问题的固有特性,提出在模型训练过程中使用较小的辅助边界框计算损失,以对高 IoU 样本的回归产生正向效果,而低 IoU 样本产生相反效果。
作者提出了 Inner-IoU 损失,通过引入比例因子控制来生成不同尺度的辅助边界框以计算损失。将其应用于现有的 IoU 基于损失函数可以实现更快和更有效的回归结果。
作者进行了一系列仿真和比较实验,实验结果表明,作者的方法在检测性能和泛化方面优于现有方法,对于不同像素大小的数据集,它实现了 SOTA。
IoU 损失函数在计算机视觉任务中有广泛的应用。在边界框回归过程中,不仅可以评估回归状态,还可以通过计算回归损失来加速收敛。在这里,作者讨论 IoU 变化与边界框大小之间的关系,分析边界框回归问题的本质特征,并解释本文提出方法的可行性。
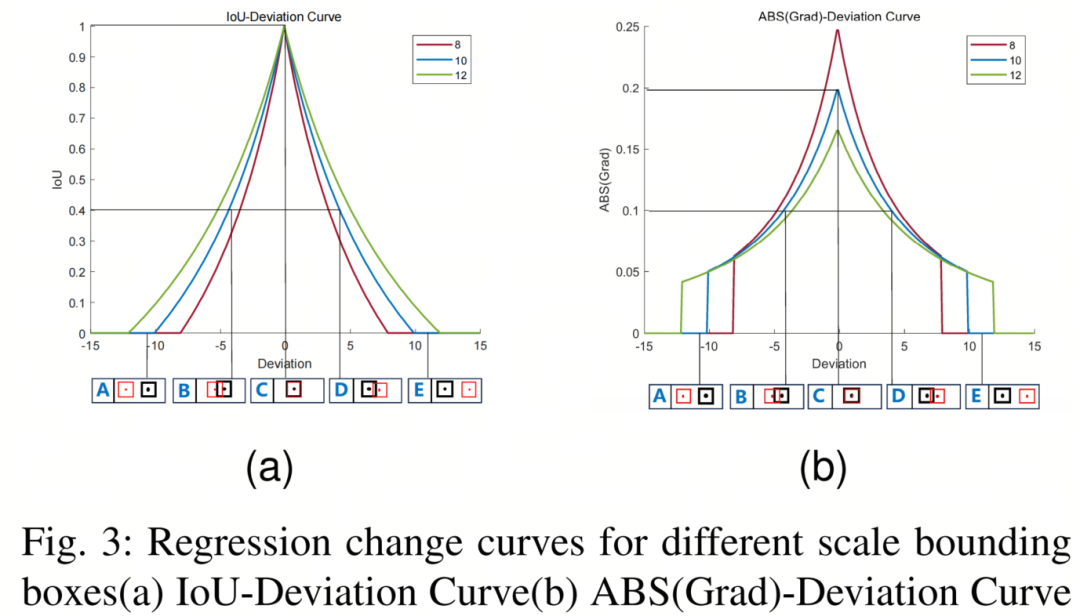
如图 3 所示,图 3a 显示了 IoU 偏差曲线,水平轴和垂直轴分别表示偏差和 IoU 值。三种不同颜色的曲线对应不同尺度边界框的 IoU 变化曲线。A、B、C、D 和 E 分别表示Anchor框和 GT 框的 5 种不同位置关系,其中红色边界框表示长度和宽度为 10 的Anchor框,对应的 GT 框用黑色边界框表示。
图 3b 显示了 ABS(Grad)偏差曲线。与图 3a 不同,图 3b 的垂直轴表示 IoU 偏差的绝对值。作者假设实际边界框大小为 10,使用大小为 8 和 12 的边界框作为辅助边界框。在图 3 中,A 和 E 对应低 IoU 样本的回归状态,而 B 和 D 对应高 IoU 样本的回归状态。从图 3 可以得出以下结论:
由于辅助边界框与实际边界框之间的尺度差异,回归过程中 IoU 值的变化趋势与实际边界框 IoU 值的变化趋势一致,可以反映实际边界框回归结果的质量。
对于高 IoU 样本,较小尺度辅助边界框的 IoU 偏差的绝对值大于实际边界框 IoU 偏差的绝对值。
对于低 IoU 样本,较大尺度辅助边界框的 IoU 偏差的绝对值大于实际边界框 IoU 偏差的绝对值。
基于以上分析,使用较小尺度辅助边界框计算 IoU 损失有助于提高高 IoU 样本的回归速度并加速收敛。相反,使用较大尺度辅助边界框计算 IoU 损失可以加速低 IoU 样本的回归过程。
为弥补现有 IoU 损失函数在不同的检测任务中的泛化能力较弱且收敛速度较慢的不足,作者提出使用辅助边界框计算损失以加速边界框回归过程。在 Inner-IoU 中,作者引入了尺度因子比,可以控制辅助边界框的尺度大小。通过为不同数据集和检测器使用不同尺度的辅助边界框,可以克服现有方法在泛化能力方面的局限。
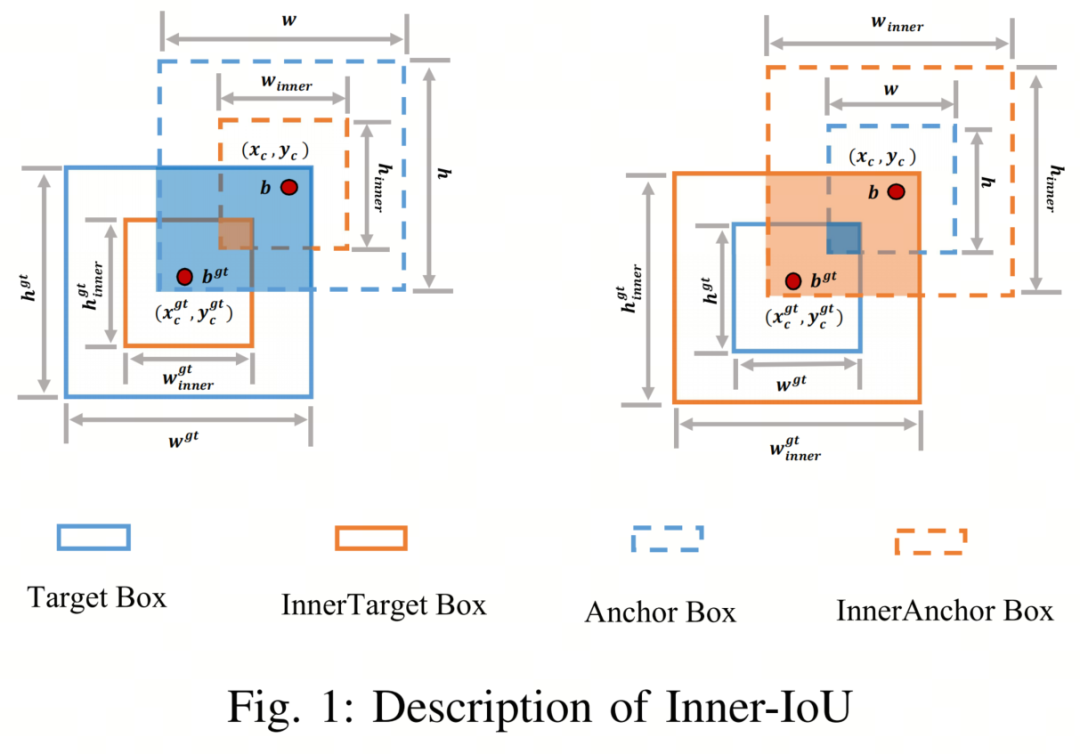
GT框和Anchor框分别表示为 和 B,如图 1 所示。GT 框的中心点和内 GT 框的中心点用表示,而 代表Anchor框和内Anchor框的中心点。GT 框的宽度和高度分别用 和 表示,而Anchor框的宽度和高度用 和 表示。变量“ratio”对应缩放因子,通常在 [0.5, 1.5] 的范围内。
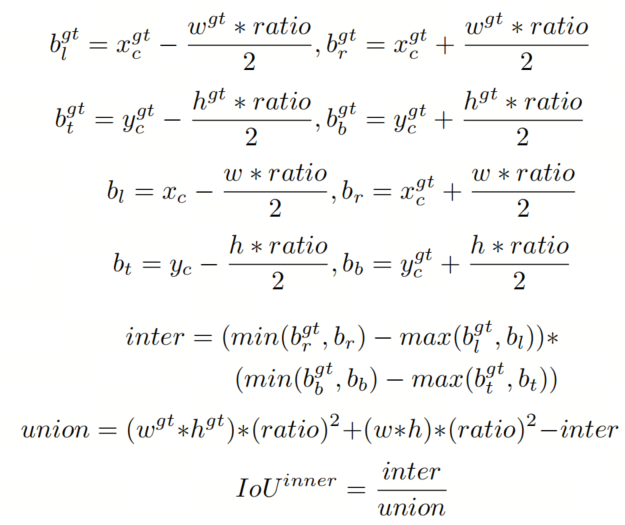
Inner-IoU 损失继承了 IoU 损失的一些特征,同时具有自己的特点。Inner-IoU 损失的范围与 IoU 损失相同,为 [0,1]。由于辅助边界框与实际边界框之间仅存在尺度差异,损失函数的计算方法相同,Inner-IoU 偏差曲线与 IoU 偏差曲线相似。
与 IoU 损失相比,当比例小于 1 且辅助边界框尺寸小于实际边界框时,回归的有效范围小于 IoU 损失,但梯度的绝对值大于从 IoU 损失获得的梯度,可以加速高 IoU 样本的收敛。相反,当比例大于 1 时,较大尺度的辅助边界框扩展了回归的有效范围,对低 IoU 样本的回归具有增强效果。
将 Inner-IoU 损失应用于现有的基于 IoU 的边界框回归损失函数,如 、、、、 和 ,如下所示:
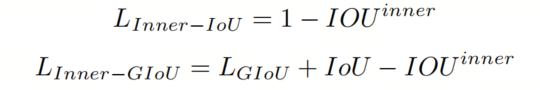
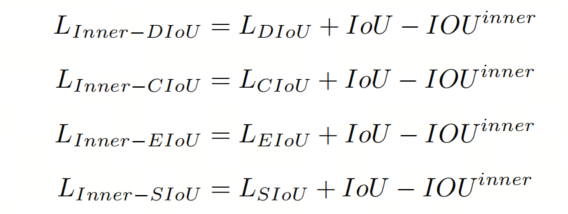
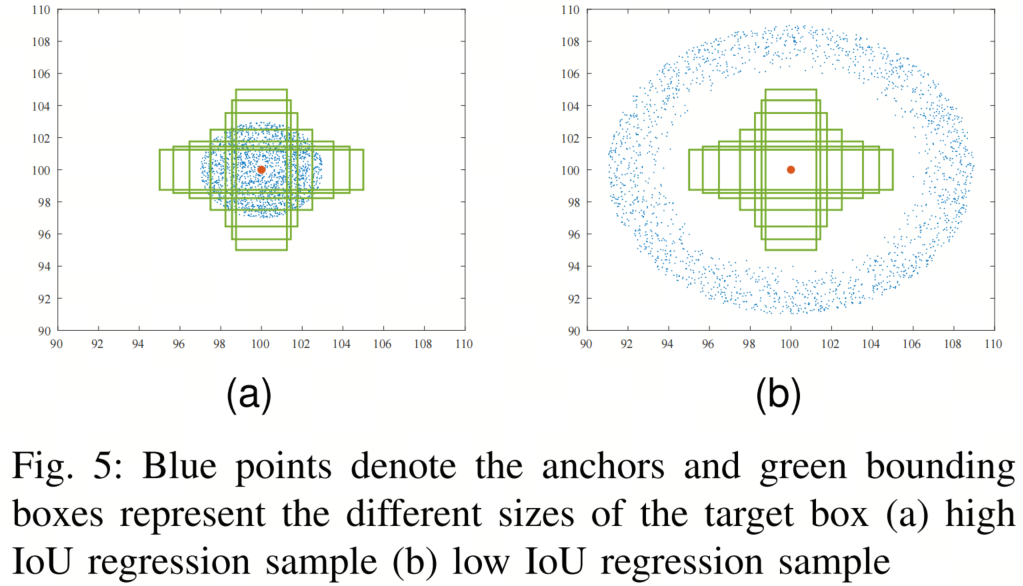
如图 5 所示,本文通过模拟实验分析了两种不同场景下的边界框回归过程。在图 5a 和图 5b 中,设置了7个不同的绿色边界框作为目标框,目标框的中心点设置为(100,100),比例分别为 1:4、1:3、1:2、1:1、2:1、3:1 和 4:1。在图 5a 中,Anchor框随机分配 2000 个点,其位置分布以(100,100)为中心,半径为 3。对于每个点的尺度,Anchor框的面积设置为 0.5、0.67、0.75、1、1.33、1.5 和 2。
对于给定的点和尺度,适应 7 个 aspect ratios,即遵循与目标框相同的目标设置(即 1:4、1:3、1:2、1:1、2:1、3:1 和 4:1)。图 5b 的Anchor框分布不同于图 5a,其位置分布以(100,100)为中心,半径为 6 至 9。尺寸和比例与图 5a 相同。总之,在每个实验中,应将 2,000 × 7 × 7 个Anchor框拟合到每个目标框。
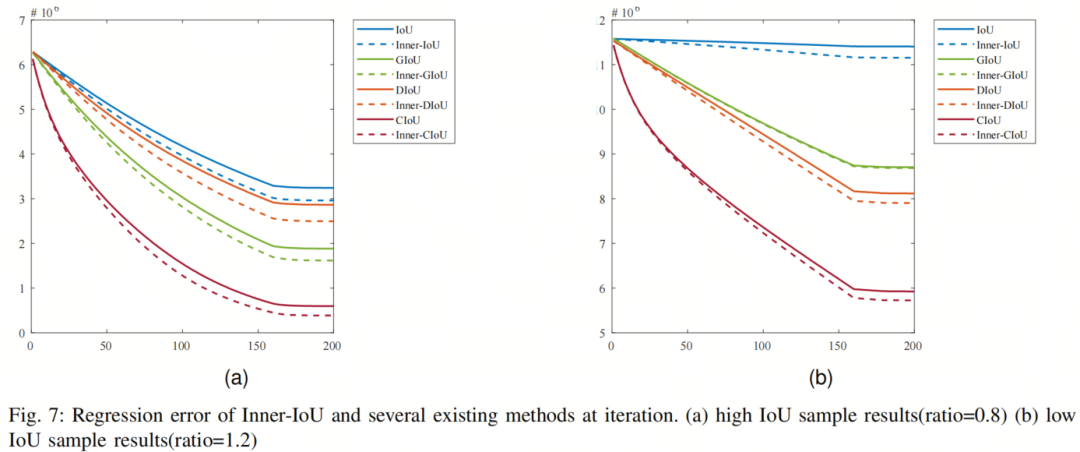
因此,总共有 686,000=7 × 7 × 7 × 2,000 种压缩情况。模拟实验的结果如图 7 所示,其中图 7a 表示高 IoU 回归样本场景下的收敛结果。为了加速高 IoU 样本的回归,尺度因子比例设置为 0.8。图 7b 表示低 IoU 回归样本场景下的收敛结果,比例设置为 1.2。可以看出,图中表示作者方法的虚线收敛速度优于现有方法。
本实验对比了 CIoU 方法和 SIoU 方法,使用 YOLOV7-tiny 作为检测器,VOC2007 trainval 和 VOC2012 trainval 作为训练集,VOC2007 test 作为测试集。训练集包含 16551 张图像,而测试集包含 4952 张具有 20 个类别的图像。作者在训练集上训练了 150 个Epoch,以展示作者方法的优势。
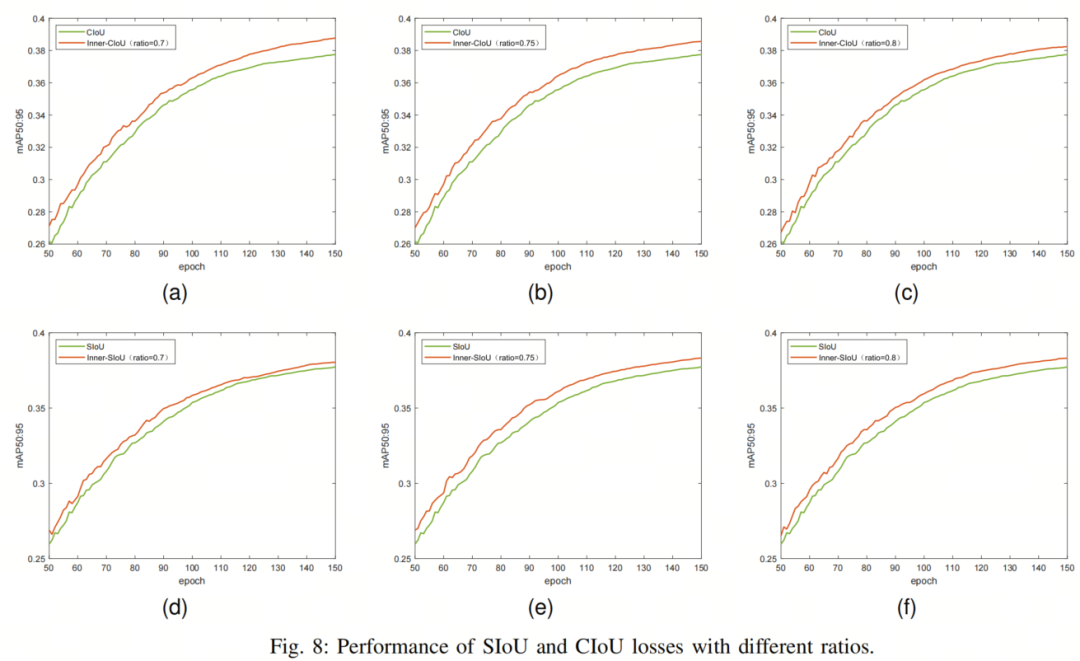
作者可视化了所提出方法与原始方法的训练过程,如图 8 所示。图 8a、图 8b 和图 8c 分别显示了 CIoU 和 Inner-CIoU 的训练过程曲线,相应比例分别为 0.7、0.75 和 0.8。图 8d、图 8e 和图 8f 分别为 SIoU 和 Inner-SIoU 在比例为 0.7、0.75 和 0.8 时的训练过程曲线。
在图 8 中,橙色曲线代表本篇论文提出的方法,而现有方法用绿色曲线表示。可以看出,在 50 到 150 个Epoch的训练过程中,本文提出的方法优于现有方法。
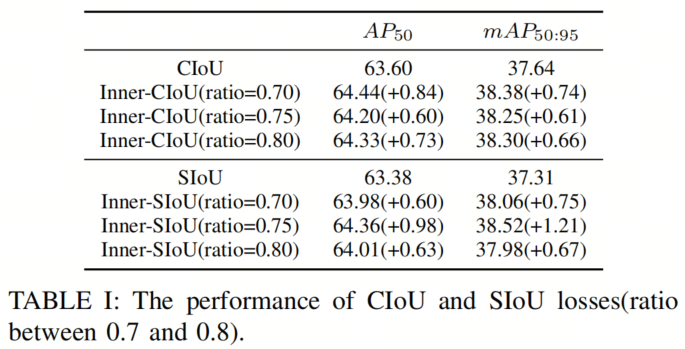
对比实验在测试集上的结果如表 1 所示。可以看出,应用本文方法后,检测效果得到了提高,AP50 和 mAP50:95 均提高了 0.5% 以上。

图 2 和图 6 展示了检测样本的比较。从图中可以看出,与现有方法相比,所提出的方法定位更准确,假检测和漏检测较少。

为了证明所提出方法的可泛化性,作者在 AI-TOD 数据集上进行了比较实验,使用 SIoU 作为比较方法。
AI-TOD 包括 28036 张空中图像,8 种目标类型,以及 700621 个目标实例,其中 14018 张图像作为训练集,其余 14018 张图像作为测试集。与现有的目标检测任务数据集相比,AITOD 的平均大小为 12.8 像素,远小于其他数据集。实验结果如表 II 所示。
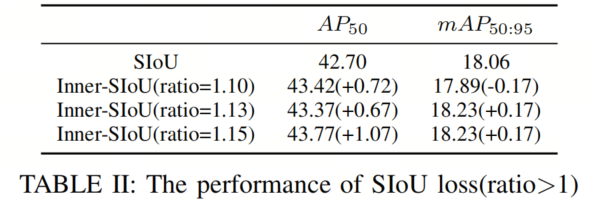
在对比实验 1 中,通过将比例值在 0.7 和 0.8 之间设置为小于 1,生成了一个比实际边界框小的辅助边界。实验结果表明,它可以提高高 IoU 样本的收益。在实验 2 中,当比例值大于 1 时,通过生成更大的辅助边界框来加速低 IoU 样本的收敛。

此外,图 4 展示了测试集上的检测结果比较,通过比较可以看出所提出方法的优势。
[1]. Inner-IoU: More Effective Intersection over Union Loss with Auxiliary Bounding Box.

点击上方卡片,关注「集智书童」公众号
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢