ICLR2023 | 基于能量受限扩散的可扩展transformer

编译 | 曾全晨

审稿 | 王建民

今天为大家介绍的是来自严骏驰教授团队的一篇论文。现实世界数据生成通常错综复杂，与标准学习方法中的独立同分布数据假设相去甚远，这对于揭示学习实例表示的几何结构构成了挑战。为此，作者引入了一种能量受限扩散模型，通过它们的相互作用将数据集中的实例信息相互传递。实验证明了作者的模型在各种任务中作为通用编码器的广泛适用性，具有出色的性能。

现实世界的数据是从复杂的交互过程中生成的，其潜在原理通常是未知的。这种性质与标准表示学习范式的常见的数据是独立同分布的假设不同。然而，由于缺乏关于真实数据生成的先验知识，实际上很难建立可行的方法来揭示数据之间的依赖关系。为了解决这个问题，以前的研究人员考虑对实例之间的潜在相互作用进行编码，但这需要足够的自由度，会显著增加从有限标签中学习的难度。研究人员转向将实例关系被抽象化成图的方法，并且目前已经在设计具有表达力架构方面取得了显著进展，例如图神经网络（GNNs）。然而，观察到的关系可能是不完整/有噪声的。观察到的数据关系与底层数据几何形态之间的潜在不一致可能导致基于图形学习的结构化表示和真正的数据依赖之间的系统偏差。

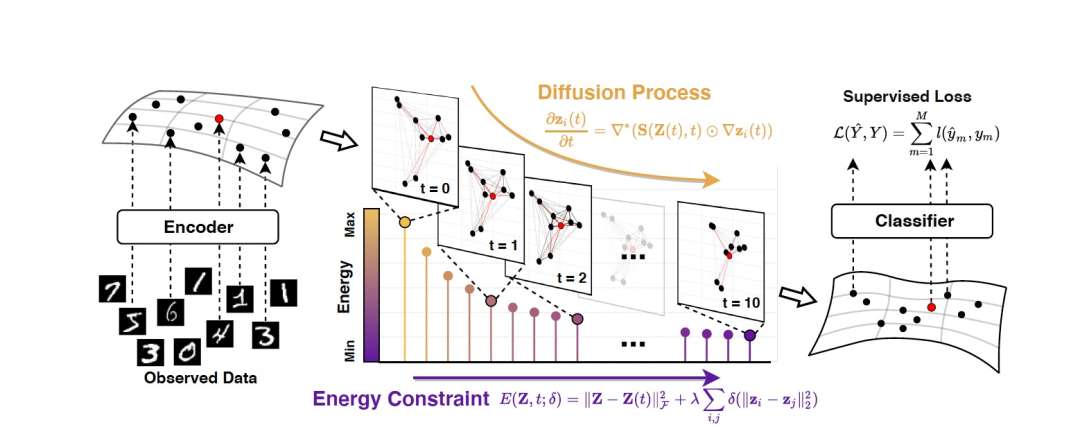
图 1

为了解决这个困境，作者提出了一种新颖的通用编码器框架（如图1所示），从观测数据（部分标记实例的数据集）中揭示数据依赖关系。作者的模型基于前馈连续动态（偏微分方程）来设计，其中数据集中的所有实例被视为黎曼流形上的位置，具有潜在结构，而实例的特征则像热量一样流过底层的几何结构。它的主要优势在于扩散的灵活性，即信息传播速率的度量：允许在每个层中的任意实例对之间进行特征传播，并通过成对连接权重自适应导航这个过程。此外，为了引导实例表示朝向一些内部一致性的理想约束，作者引入了一个合理的能量函数，该函数对演化方向进行逐层正则化。基于这一理论，作者提出了一类新型的神经编码器，称为DIFFORMER，并提供了两种实际的实例化版本：一种是简化版本，用于计算实例之间的所有基于数据对的交互作用；另一种是更具表现力的版本，可以学习复杂的潜在结构。

考虑一组部分标记的实例 {x_i}，它们的标记部分是 {(x_j, y_j)} (代标记的实例只占数据集的一小部分)。在某些情况下，存在将这些实例连接起来的关系结构，可以表示为一个图 G = (V, E)，其中节点集 V 包含所有实例，边集 E = {e_ij} 包含观察到的关系。在不失一般性的情况下，作者的方法不假设图结构作为输入。模型的起点是一个扩散过程，它将一组数据作为整体处理，并通过信息流产生实例表示，这些信息流的特征由各向异性扩散过程描述，此处灵感来自于在黎曼流形上的热扩散过程。作者使用一个矢量值函数 z_i(t)来定义时间 t 和位置 i 处的实例状态。各向异性扩散过程描述了实例状态的演化：

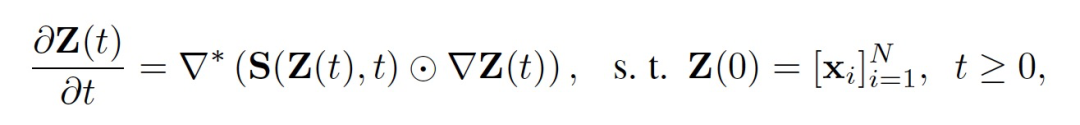
其中S(Z(t), t) 定义了扩散系数，该系数控制了在时间 t 时任意一对实例之间的扩散强度。扩散过程取决于每个实例在特定时间点 t 的状态。梯度算子 ∇ 用来衡量源状态和目标状态之间的差异。而散度算子 ∇∗ 用来对某一点上的信息流进行求和。这两个算子都是在由 N 个位置组成的离散空间上定义的。上述方程的物理含义是，在位置i的热量的时间变化等于进入该点的热通量，并且可以明确地写为：

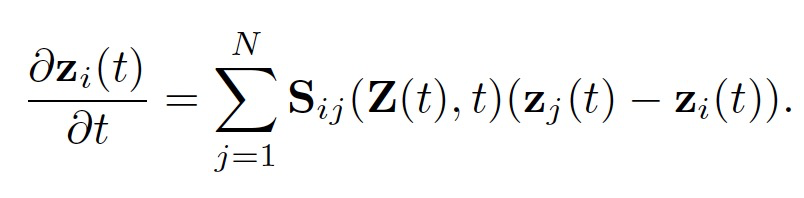
这样的扩散过程可以作为一种归纳偏见，引导模型在每一层进行实例信息交互学习。作者利用涉及步长 τ 的有限差分的显式欧拉方法对上述方程求数值解，得到：

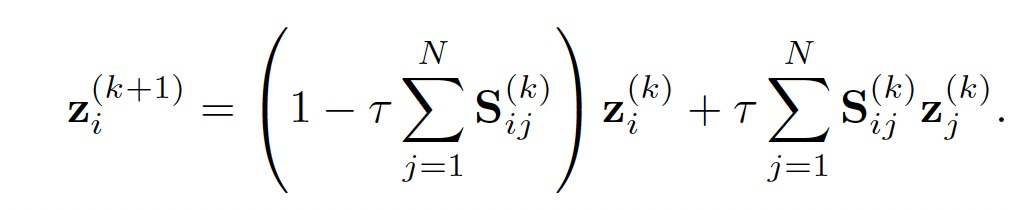
数值迭代可以在 τ ∈ (0, 1) 的范围内稳定收敛。可以采用在有限步K传播步骤之后的状态用于最终的预测。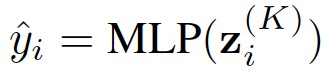

问题的关键在于如何定义一个合适的扩散率函数，以诱导一个期望的扩散过程，该过程可以最大化信息效用并符合一些内在的一致性。由于对S^(k) 的显式形式或内部结构没有先验知识，因此作者将扩散率视为时间相关的潜在变量，并引入一个能量函数，用于衡量给定步骤 k 时实例状态的预期量：

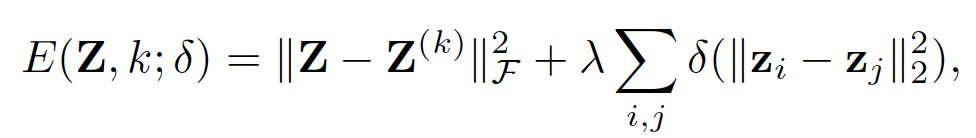
δ 被定义为在感兴趣的特定区间上是非递减且凹的函数。权重 λ 权衡了两个效应：1）对于每个实例 i，与当前状态 z_i 不远的状态具有较低的能量；2）对于所有实例，它们的状态之间的差异越小，产生的能量越低。扩散过程描述了实例状态通过演变的微观视角，而能量函数提供了一个宏观视角，用于量化一致性。一般来说，我们期望最终的状态能够产生较低的能量，这表明物理系统达到了一个稳定点。因此，作者将两种思想统一到一个新的扩散系统中，其中实例状态将朝着产生更低能量的方向演变，目标是找到一系列 S^(k) 的动态传递和能量约束，满足如下所示：

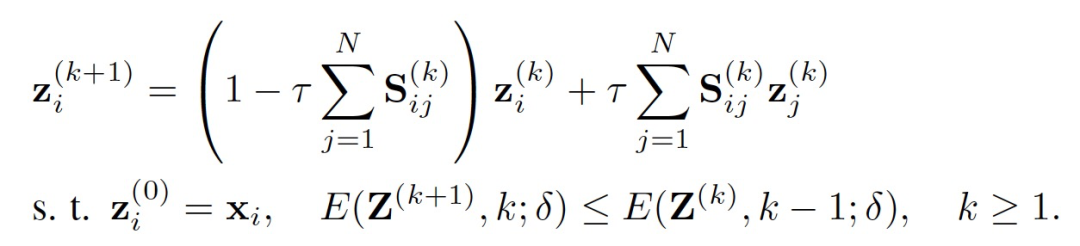
该公式引导了一类新的几何流动，这些流动发生在潜在流形上，其动态是通过优化时变能量函数来隐式定义的（图1）。

文章的关键贡献是以下定理，揭示了几何扩散模型与能量迭代最小化之间的潜在联系，论证了基于当前状态Z^(k) 的 S^(k) 的显式闭合形式解并实现了能量的严格下降（论证过程请见文章附录B部分）：

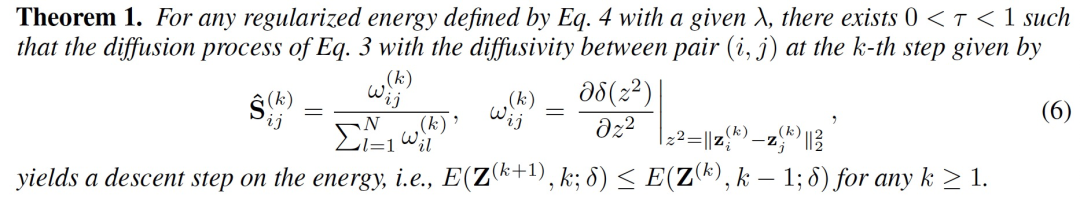
该定理论述了最优扩散的存在，其形式是当前步骤中实例状态之间的l2距离的函数。该结果使我们能够展开隐式过程，并以前馈方式从初始状态计算S^ (k)。因此得到了一类新的神经模型架构，其层次计算由以下方式指定：

在论证完可行性之后作者给出了该方法的两种实现方式，并且在附录E中贴心的给出了伪代码示例。首先，由于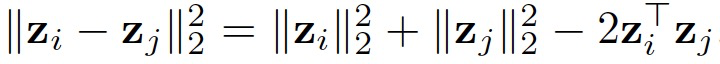，可以在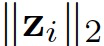为常量的条件下，通过改变变量将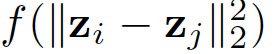转化为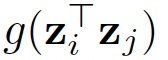的形式。第一种模型设计方案为采用线性方程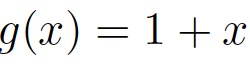来计算定理1中的：

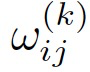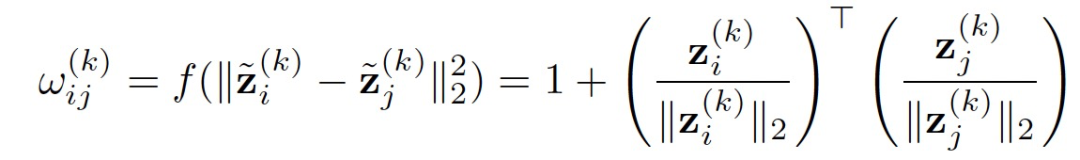
该方法的一大好处是可以重新安排计算方式大大加速计算过程，实例之间的传播计算复杂度从O（N^2）降低到O（N）：

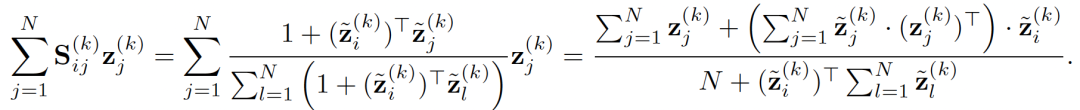
这种处理方式与作者之前发表在ICLR2022的Nodeformer相同，很适用于大型图的计算。作者将这种实现方式成为称为DIFFORMER-s。

第二种实现方式计算上稍微复杂点，但提高了模型对复杂潜在几何结构的建模能力。其计算方式如下：

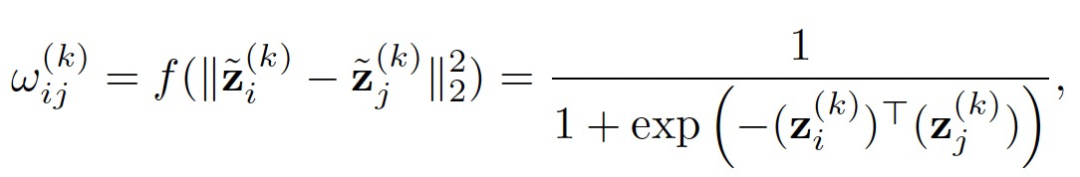
作者将这种实现方式成为称为DIFFORMER-a。

以上作者提出的模型可以应用在任意条件下。当应用者想要输入一个初始图结构时，可以稍微更改实例节点的传播方式，以符合初始图结构，具体如下：

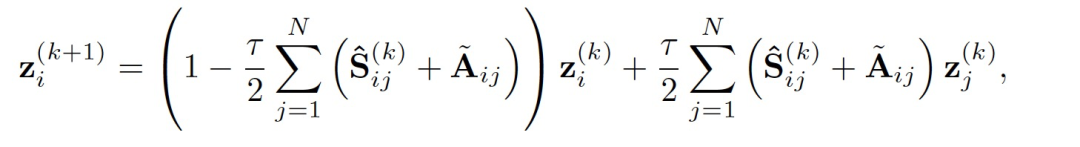
作者的理论产生了一个通用的扩散框架，将一些现有的模型统一。作为一个非详尽的比较，表1呈现了与MLP、GCN和GAT的关系。

表 1

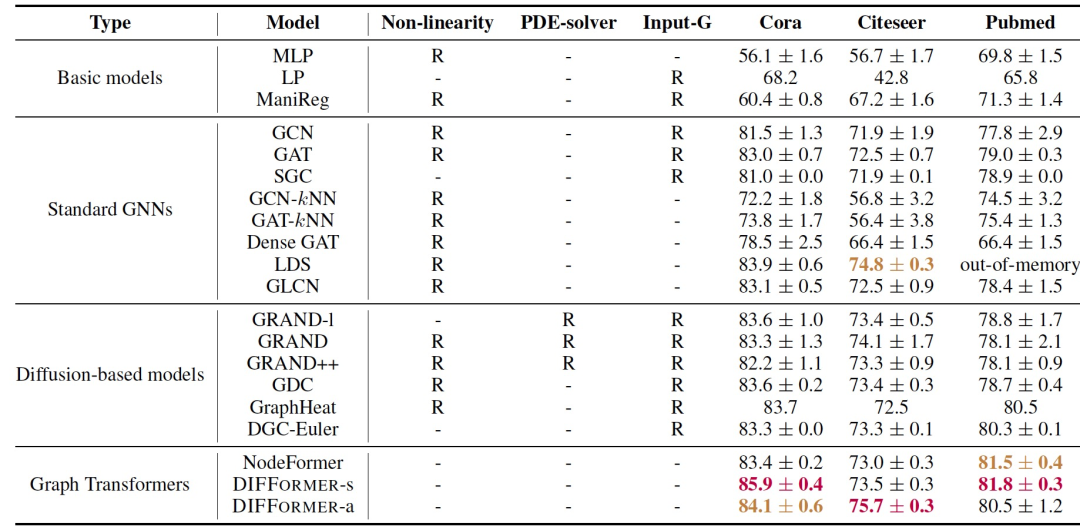
表 2

作者在三个网络Cora、Citeseer和Pubmed上测试了DIFFORMER。表2报告了测试准确性。作者与几组基线模型进行了比较，这些模型从不同方面与作者的模型相关联。表2显示DIFFORMER在三个数据集上取得了最佳结果，且改进明显。此外，作者注意到简单的扩散度模型DIFFORMER-s明显超过了没有非线性的对应模型。这些结果表明DIFFORMER可以作为用于节点级预测的非常有竞争力的编码器干，学习了生成信息丰富的表示并提高了下游应用的性能。

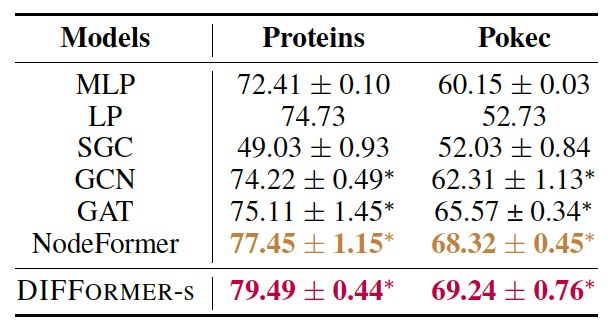
表 3

作者还考虑了两个大规模图数据集，ogbn-Proteins（一个多任务蛋白质相互作用网络）和Pokec（一个社交网络）。表3呈现了结果。由于数据集的规模（两个图的节点数分别为0.13M和1.63M）以及表2中许多方法和DIFFORMER-a可能会遇到的可扩展性问题，作者只将DIFFORMER-s与标准GNN进行比较。可以发现DIFFORMER在性能上明显优于普通的GNN，这表明它在大规模数据集上具有良好的效能。

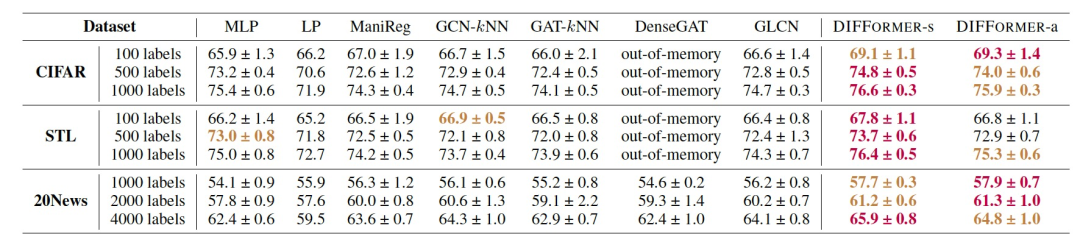
表 4

接下来，作者在CIFAR-10、STL-10和20News-Group数据集上进行实验，以测试DIFFORMER在带有有限标签的标准分类任务上的性能。对于由20News数据集，作者选择了10个主题，并使用TF-IDF值大于5的词作为特征。对于CIFAR和STL两个公共图像数据集，作者首先使用无监督的自我监督方法SimCLR（不使用标签进行训练）来训练一个ResNet-18，以提取特征图作为实例的输入特征。这些数据集不包含图结构，因此作者对于GNN竞争对手使用kNN来构建基于输入特征的图，并且对DIFFORMER不使用输入图。表4报告了DIFFORMER和包括MLP、ManiReg、GCN-kNN、GAT-kNN、DenseGAT和GLCN在内的竞争对手的测试准确性。两个DIFFORMER模型在几乎所有情况下都比MLP表现得更好，表明学习实例间相互依赖性的有效性。此外，DIFFORMER在GCN和GAT上取得了显著的改进，这些方法在某种程度上受到手工构建的图的限制，导致传播效果不佳。此外，DIFFORMER明显优于GLCN，GLCN是一种学习新（静态）图结构的强大基线，这证明了作者模型的演化扩散性在适应不同层面上的优越性。

作者提出了一个以能量驱动的扩散模型。该模型将所有实例作为一个整体，并编码成演化状态，旨在最小化能量函数，从而实现隐式的正则化。作者进一步设计了两种实现方式，可以学习底层数据几何上的复杂相互作用。大量实验证明了该模型的有效性和优越性。

Wu, Q., Yang, C., Zhao, W., He, Y., Wipf, D., & Yan, J. (2023). Difformer: Scalable (graph) transformers induced by energy constrained diffusion. arXiv preprint arXiv:2301.09474.