如何预测交通堵塞？来自复杂系统的出行指南

1. 交通堵塞的时间呈幂律分布

交通拥堵已成为影响城市健康的“顽疾”。就像生物对疾病有自愈能力一样，交通也能从各种干扰中自发恢复。基于大规模 GPS 数据集，2019年的PNAS研究揭示了交通从拥堵中恢复的行为在所有拥堵尺度上都受三个幂律定律的支配。这些无标度律与微观细节无关，包括交通需求的波动和相应的管理。

相关研究：

Scale-free resilience of real traffic jams

论文地址：

https://www.pnas.org/doi/10.1073/pnas.1814982116

不同城市的交通堵塞聚集大小（左列）与持续时间的分布，不论是北京还是深圳的二维公路网，或是一维的高速路，都呈现幂律分布。

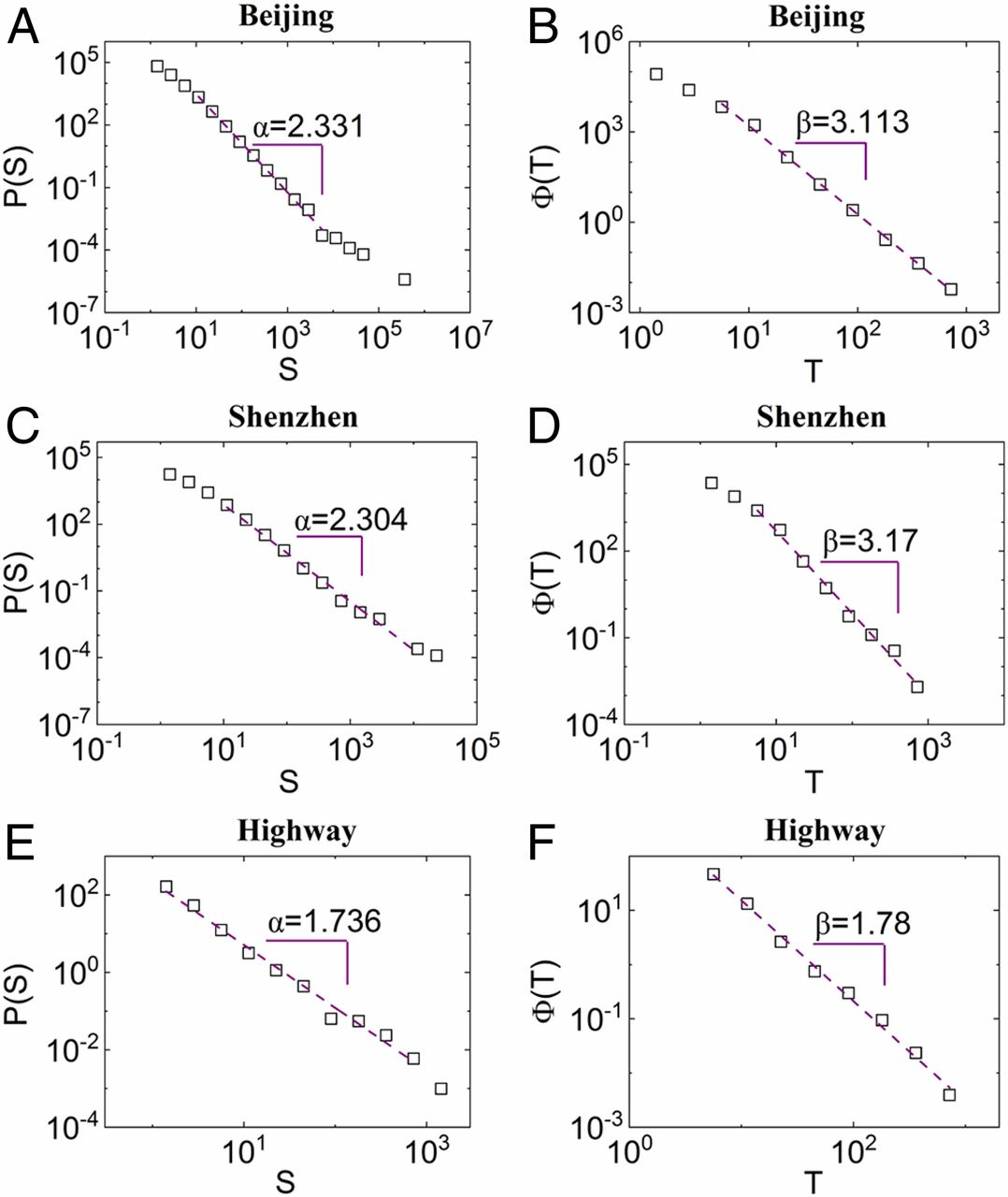
图1：交通堵塞恢复力的无标度幂律

不论是工作日还是周末，或者是圣诞节这样的节假日，交通堵塞的恢复稳定性规律不会改变。

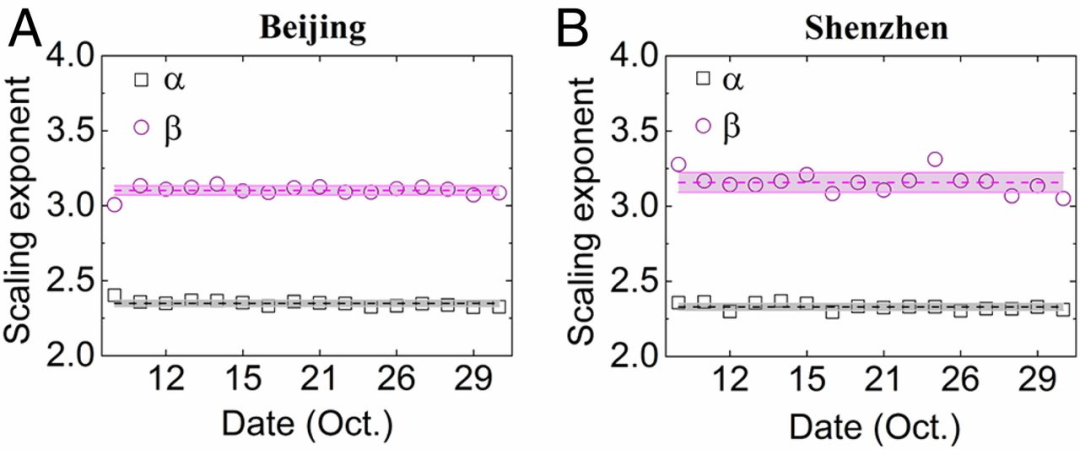
图2：不同时间的空间和时间幂律指数稳定

更大的交通堵塞所影响的空间更大，恢复所需的时间也越长。

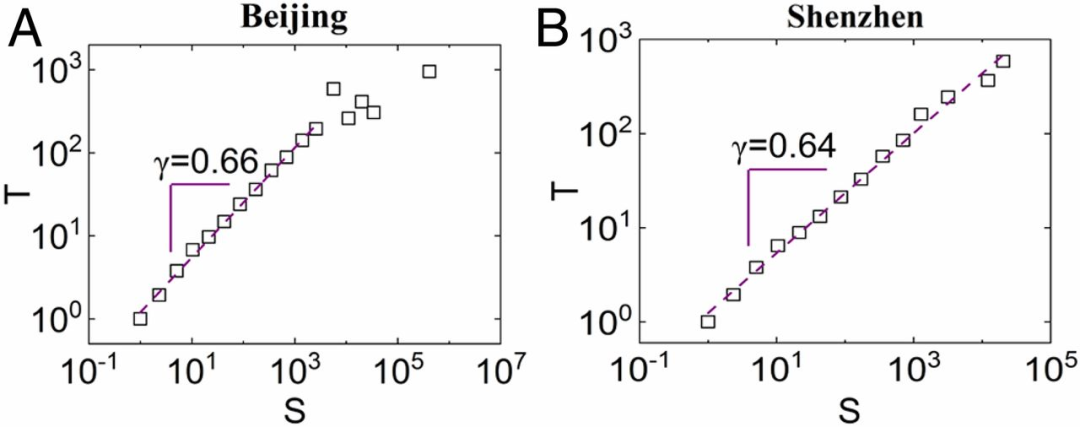
图3：交通堵塞的影响空间与持续时间之间的关系

对交通堵塞韧性符合幂律的发现，可以为更好地理解和设计这些复杂的工程系统在内部和外部干扰下的运行提供参考。

2. 交通堵塞存在多稳态

乘客所经历的不同交通状态可能是由于局部的随机拥堵，也可能是由系统对扰动的反应决定的整体网络状态。在生态学、生物学和气候学等许多领域的自然系统中都曾发生过不同状态之间的突然转变，例如生态系统的急速崩溃。

2020年的一项研究基于渗滤理论和高分辨率 GPS 数据集，发现特大城市中存在这样的多稳态及临界点，且这样的多稳态在不同日子里是相对固定的。

论文题目：

Multiple metastable network states in urban traffic

论文链接：

https://www.pnas.org/doi/10.1073/pnas.1907493117

该研究关注的是城市交通中，有多少区域还没有完全堵塞从而可以视为一个连通的区域，图4中早上7:41的北京，被分为很多相互不连通的区域，其中最大的一部分占比不到0.25，而7分钟之后，全市的交通看起来有50%以上是联通的。将最大联通区域占比绘制散点图，可看出其明显存在分离，意味着交通堵塞存在多个稳定态。

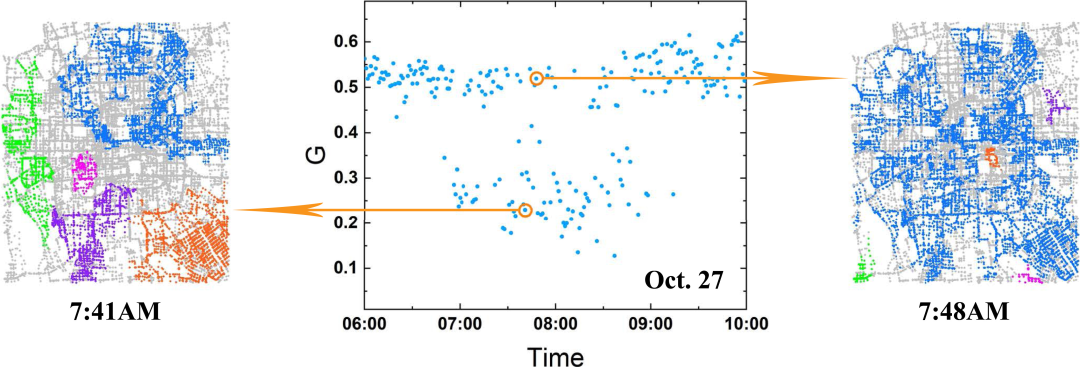
图4：不同时间段的最大联通区域示意及散点图

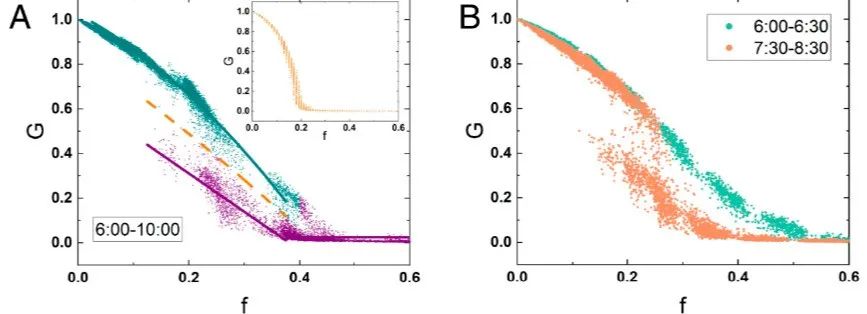
图5：早高峰时北京的最大联通区域占比的分布符合多稳定态的理论预期

基于渗流模型，可依据给定（已有）数据对临界点进行预测，预测的临界点与真实数据的差值呈幂律分布（图6a），说明真实情况下影响因素可能为多因素混合，工作日的系统临界点分布也存在双峰（图6b）。由于多稳态下，常常存在迟滞效应（hysteresis），故而如图6c中所示，变化是不连续的，而渗流模型预测的临界点也对应了真实场景下突变发生的那一点。

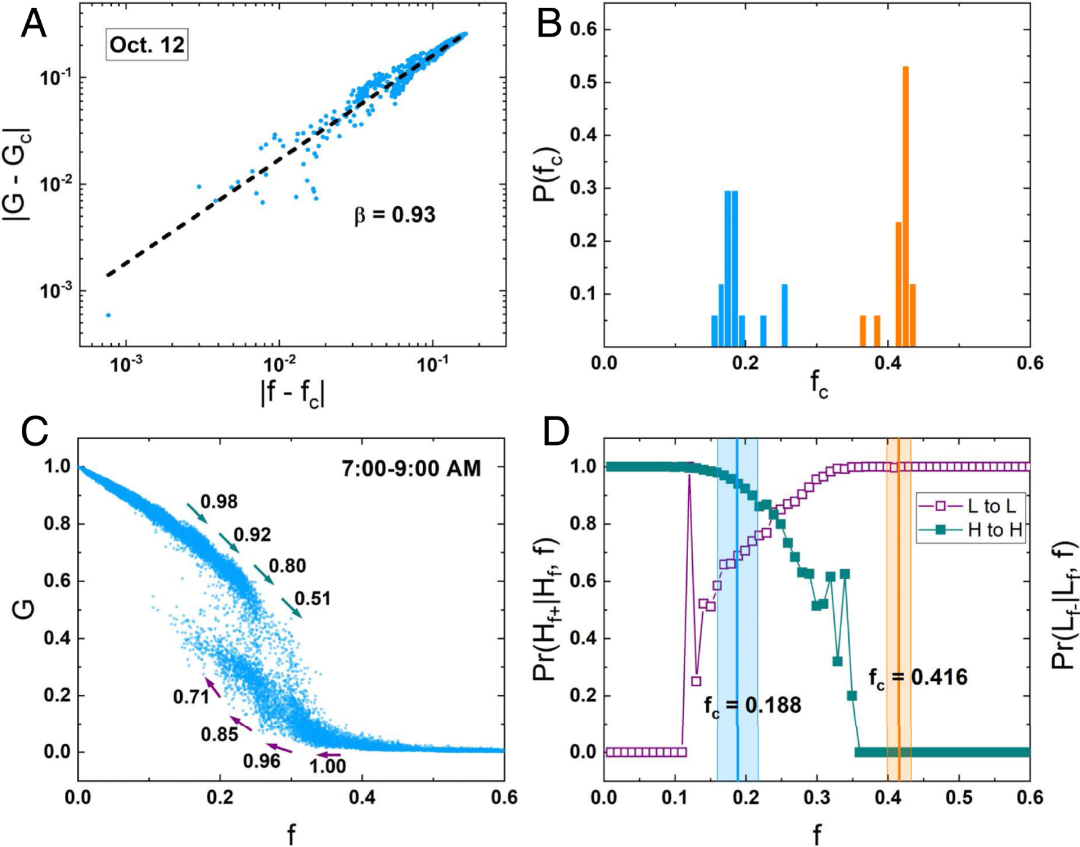
图6：渗流模型预测的临界点与真实数据

之所以会出现多稳态，是由于交通拥堵会出现长程相关性，而长距离联系可以决定网络的整体流量传导性。理解了上述现象，结合渗流模型，就可以帮助城市管理者设计预警信号，防止系统进入严重拥堵状态。例如对瓶颈区域实施更具体的交通信号控制或对进入拥堵区域收费，以动态调整交通流量。

3. 交通堵塞可通过SIR模型描述

前述研究考虑的是工作日早高峰时处处都拥堵的情况。而像由于演唱会等非日常事件引起的堵车，则可通过流行病领域的SIR模型（易感-感染-恢复）对其建模。

2020年的研究，为网络交通动力学引入了两个宏观特征，即拥堵传播率 β 和拥堵消散率 μ。通过使用这些嵌入常微分方程系统的新参数来描述拥塞传播的动力学，这与著名的SIR模型类似。通过多城市实证分析，可验证所提出的基于传染的动力学模型，可用于监测、预测和控制网络中随时间变化的拥塞链路比例。

论文题目：

A simple contagion process describes spreading of traffic jams in urban networks

论文链接：

https://www.nature.com/articles/s41467-020-15353-2

网络中拥塞的积累程度和恢复速度取决于基本再生系数 R0 所代表的传播率与恢复率之比。在任何给定的 ρ 条件下，当需求增加时，R0 也会增加，这清楚地表明交通堵塞的规模会越来越大，并且需要更长的时间来恢复出行需求。

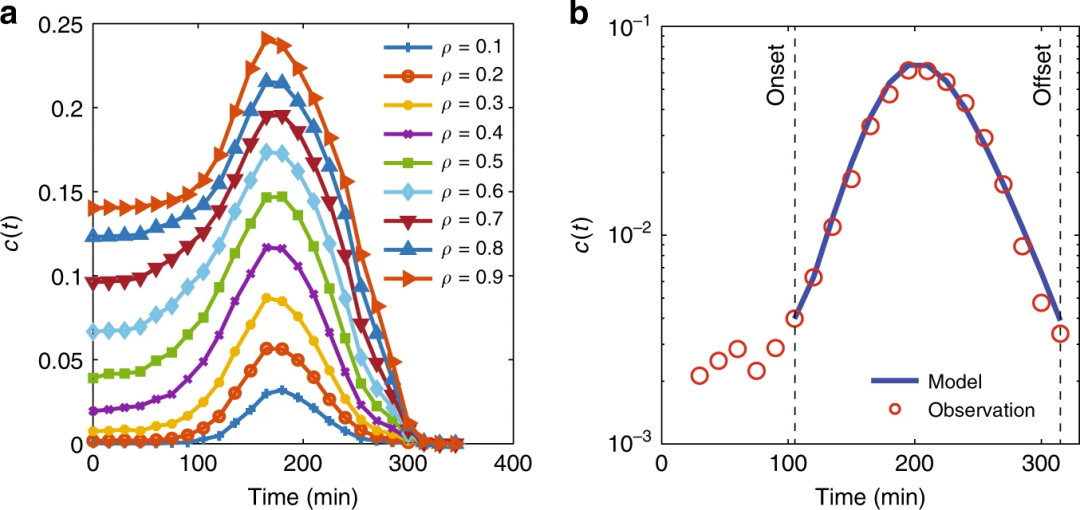
图7 模型不同参数下交通堵塞持续时间的分布与墨尔本真实分布于模型预测的对照

通过对6个城市的对比，发现不同城市在小 ρ 值下的 R0 惊人地相似，这表明在宏观层面上，这些城市的拥堵传播动力学趋于一致。

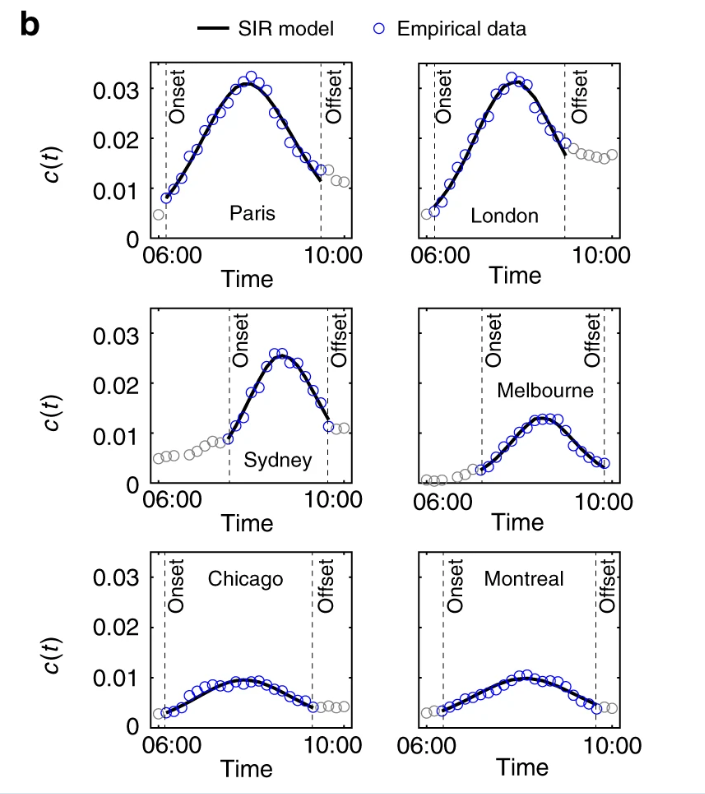
在经典的 SIR 模型中，当受感染的个体恢复后，不会再次受到感染。这显然不能直接适用于交通网络，因为在交通网络中，链路可能在短时间内恢复并再次拥塞。不过，如果分析的时间聚合足够大，则该假设仍可能成立。这也是为何说该模型可能不适合早高峰这样一条路刚通畅没多久又堵上的情况。

4. 交通堵塞的预测要趁早

由于交通动力学的复杂性，严重交通堵塞很难预测。了解交通瓶颈的网络动力学有助于避免严重交通堵塞，改善整体交通状况。而最近的一篇 Nature Communications 研究开发了一种基于早期传播阶段预测严重拥堵的方法。其框架遵循交通堵塞的网络传播和消散过程，这些过程源于瓶颈的出现、增长及其恢复和消失。

论文题目：

Spatiotemporal dynamics of traffic bottlenecks yields an early signal of heavy congestions

论文链接：

https://www.nature.com/articles/s41467-023-43591-7

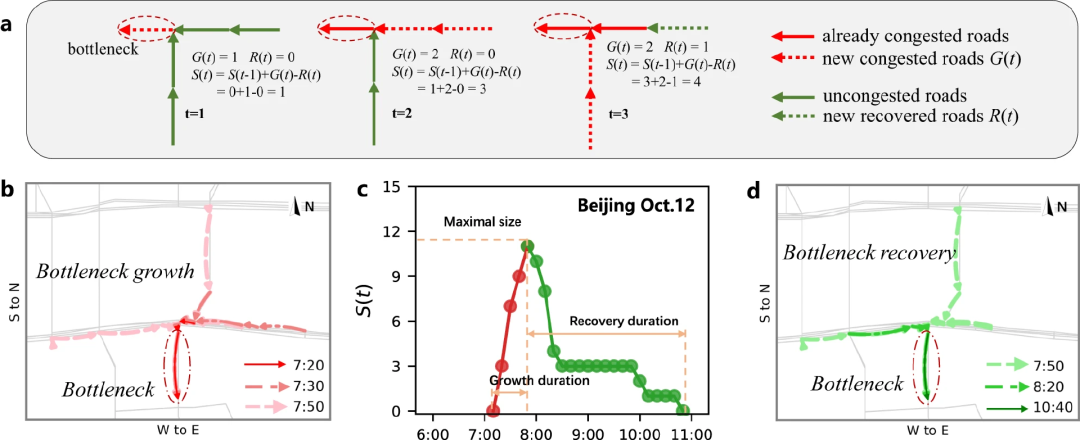
图9：交通堵塞中的瓶颈路段的拆分

预测的基础，在于整个网络中的宏观交通拥堵是由众多分散的拥堵成分组成的，而这些拥堵成分可能是由特定的瓶颈造成的，因此可以通过识别瓶颈的时空动力学来改善整体交通状况。识别交通瓶颈不仅有助于避免自身拥堵，还能缓解因网络传播而造成的其他相关拥堵道路。

基于大规模城市交通速度数据，可发现交通拥堵的消散时间近似于幂律分布，通常情况下，交通拥堵的消散速度比其增长速度慢近一倍。

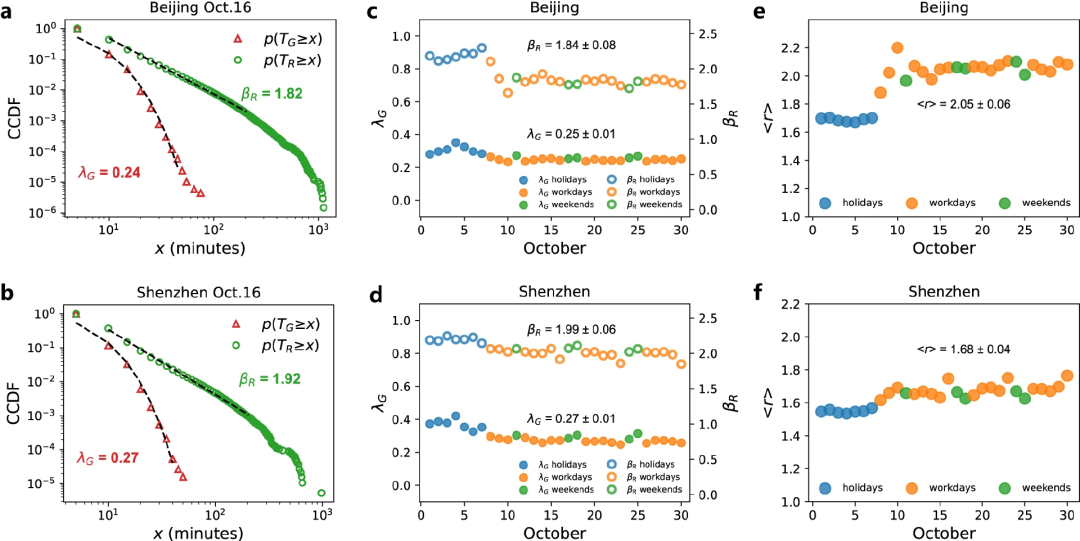
图10：北京和深圳交通堵塞发生和恢复时间及幂律系数的散点图

最佳的预测时间，是在拥堵发生的最初 15 分钟，其增长速度也与拥堵的最大规模高度相关，这意味着可以在交通堵塞前15分钟，根据瓶颈预测交通堵塞所持续的时间。

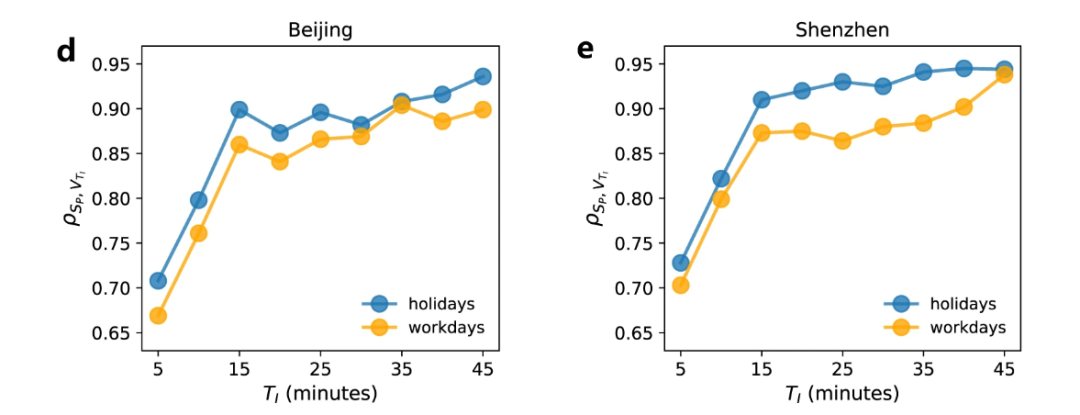
图11：堵塞开始之后经过的分钟数与其交通堵塞最大规模的相关系数

这里提供的机器学习模型可应用于城市交通控制系统，以预测严重的交通瓶颈，并在其扩散为大规模网络拥堵之前加以预防。

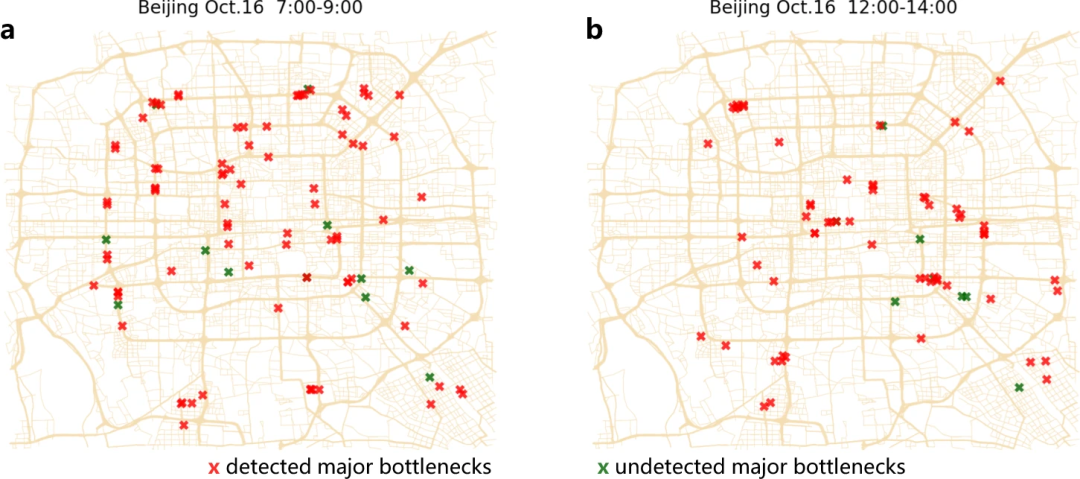
图12：预测得出的主要瓶颈路段，其中红色为成功预测

5. 总结与展望

对交通堵塞的研究，从方法论上，有借鉴元胞自动机、级联失效及多道变道等多种方式，也有考虑人与系统互动，例如有研究基于主体对人们避开堵塞路段这一博弈行为及其影响进行建模（参考《来自复杂系统的出行指南》 ）。而复杂系统的研究利用临界、渗流、传播等工具，抽离了不同地区交通堵塞的特殊性，例如道路宽度、车辆类型等因素，先对现象进行一般性描述，之后再给出基于模型描述机制的预测模型。

从数据来看，现有研究所依据的数据多来自车辆的高精度GPS定位，而随着5G的普及，可通过手机定位进行建模，从而扩大数据量。随着人工智能的兴起，可以将交通堵塞预测模型用于感知和控制交通状况，同时与附近的智能汽车进行交互，并以近乎实时的方式警告旅客避开可能导致严重交通瓶颈的道路，同时提供替代路线。

空间拥堵传播会严重影响不同信号交叉口之间的协调控制性能。根据确定的时空传播机制，实时控制系统可考虑不同交通区域之间的相互关系，并在最拥堵区域的拥堵扩散到全局性堵塞之前，对其实施更好的协调控制。城市管理者可给予预测结果，调整道路定价策略，为没有替代路线的潜在旅客重新安排出发时间，以减少预测区域的交通需求。

相关读书会推荐

城市科学读书会：空间网络与空间认知（北京大学助理教授董磊老师）

重点介绍了空间网络的基本概念、实证研究和常用模型，以及信息熵视角下的城市、空间认知和导航模型。

https://pattern.swarma.org/study_group_issue/513

相关课程推荐

城市交通的健康管理（北京航空航天大学研究员李大庆老师）

基于渗流理论，结合交通路况数据，对交通拥堵从产生、演化到恢复的全寿命周期的分析，挖掘系统的弹性规律，希望可以为城市交通的可靠性管理提供新途径。

https://campus.swarma.org/course/1020