【新智元导读】最近的数学圈,都被椭圆曲线的murmuration(椋鸟群飞)现象震惊了。由经验不足的本科生无意中做出的这个成果,竟让一位华人数学家离「千禧年问题」更近了一步。而且这次数学难题的破解,是由AI来完成的!
这次数学家们用AI发现的,是椭圆曲线中的murmuration(椋鸟群飞)现象。他们发现,如果以正确的方式观察,在椭圆曲线中会出现像飞行中的椋鸟群一般的图案。现在,murmuration相关研究已经轰动了数学圈,每周都有相关新研究问世。椭圆曲线的数据,恰巧按照conductor来排序;一个经验不足的本科生,恰巧没有处理某个数值,让曲线的震荡极为明显;按照conductor预排序的数据集,恰巧被人提前做了出来……任何一个要素的变动,都会导致人类与这一重要的数学发现失之交臂,或许再晚上几十年……并且,被陶哲轩认证的说法再次被证实:数学家们要做好准备了,AI将在十年内,赶上甚至超过最优秀的人类数学家!
它看似简单,却是把高中数学连接向深奥的数学研究的一条快速通道。它是1990年代Andrew Wiles证明费马大定理过程中的核心,还是现代密码学的关键工具。在2000年,克莱数学研究所将椭圆曲线统计特性的一个猜想,列为七大「千禧年问题」之一,悬赏100万美元的奖金。在1960年代,这一猜想被数学家Bryan Birch和Peter Swinnerton-Dyer提出,至今尚未得到证明。因此,深入探索椭圆曲线,已经成为了数学领域的一项重要的高风险任务。在2022年,数学家利用统计技术和AI,竟然在椭圆曲线上发现了一些出乎意料的全新特性!他们发现:如果以正确的方式观察,椭圆曲线就能「像椋鸟成群结队一样飞翔」。任教于普林斯顿大学和高级研究院的数学家Peter Sarnak表示:「机器学习总会给我们带来一些意料之外的惊喜!」椭圆曲线上为什么会出现这些特性呢?刚发现时,许多数学家感到非常困惑。近期的一些研究发现,这些类似椋鸟群飞翔时不断变化的形状(murmuration),并不仅仅是2022年研究中的特例,而是椭圆曲线普遍的共性。
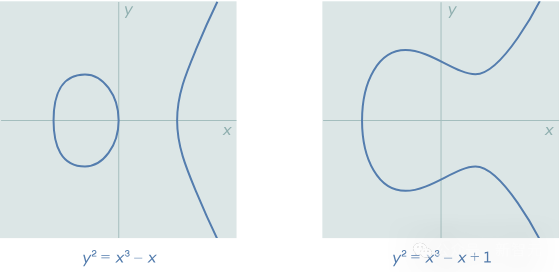
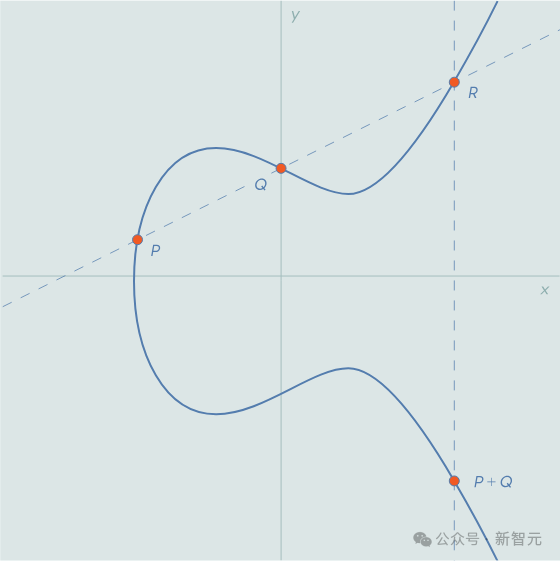
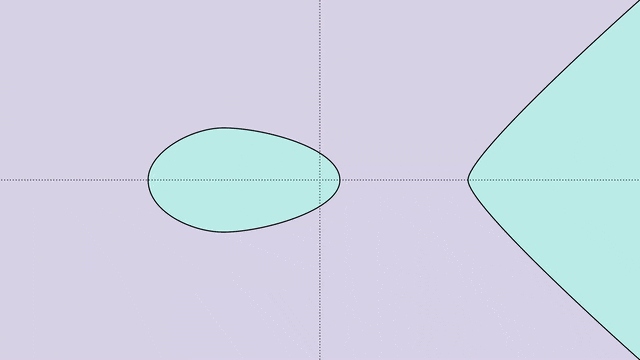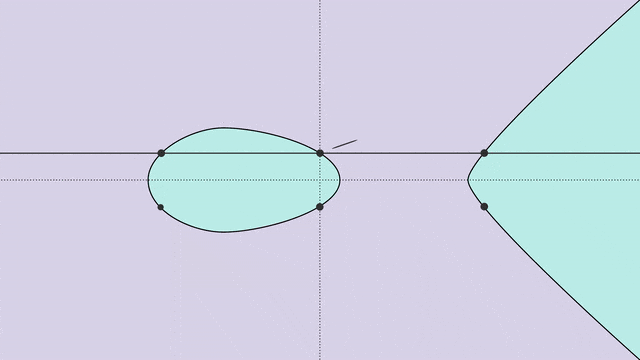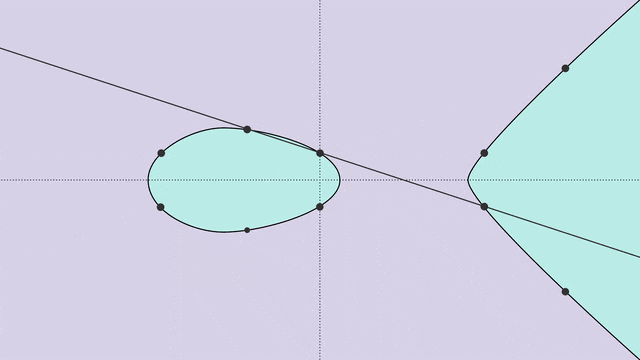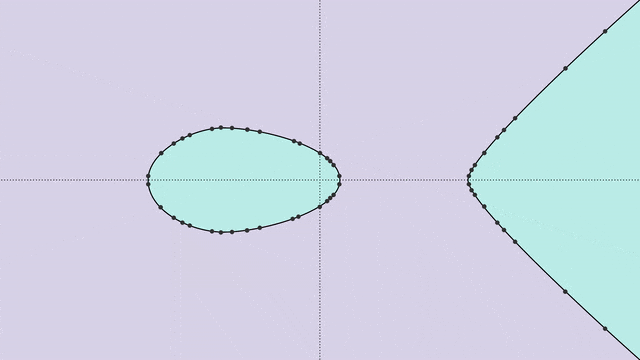
要弄明白这些模式究竟是什么,我们首先得对椭圆曲线及其分类有所了解。椭圆曲线是通过一个变量(通常用y表示)的平方与另一个变量(通常用x表示)的三次方之间的关系来定义的:y^2=x^3+Ax+B,这里的A和B是满足几个简单条件的一对数值。椭圆曲线方程定义了一条可以在平面上绘制的曲线,如下所示。虽然看起来很普通,但对于数论学者来说,椭圆曲线却是非常强大的工具。这是因为,数论学者需要在整数中寻找规律。他们不喜欢让变量x和y所有数字中取值,而是希望将它们限制在特定的数系中,也即在给定的数系上定义一个曲线。而仅限于有理数的椭圆曲线,在数论的研究中格外有用。普林斯顿数学家Sarnak说,「实数或复数域上的椭圆曲线非常单调,真正有深度的,是定义在有理数域上的椭圆曲线。」如果我们在椭圆曲线上任意两个有理点之间画一条直线,那么这条线再次与曲线相交的位置,也会是有理点。利用这个性质,我们可以在椭圆曲线上定义一种「加法」运算,如下图所示。在点P和点Q之间画一条直线,这条直线将与曲线相交于第三点R。(如果这条直线不与曲线相交呢?数学家们就会巧妙地添加一个「无穷远处的点」。)接下来,就是见证奇迹的时刻——R沿x轴的镜像点,就是P+Q的和!结合这种加法运算,曲线的所有解,就形成了一种称为「群」的数学对象。曲线的秩反映了它拥有的有理数解的数量:秩为0的曲线只有有限个解,而那些秩较高的曲线,则有无限个解。秩的概念不是那么容易理解。数学家并不总是有办法计算出秩的数值,也不能确定它的最大值能达到多大。(目前已知的某个特定曲线的最大精确秩是20。)此外,椭圆曲线还与质数(只能被1和自身整除的数)有着紧密的联系。我们可以把有限域想象成一个时钟,其「小时数」就等同于该质数:到达这个质数时如果你继续往后数,数字就会从0开始。例如,在质数7构成的有限域中,5加2的结果是0,5加3的结果是1。每个椭圆曲线,都有一个称为a_p的数列,这个序列反映了由质数p定义的有限域内椭圆曲线的解的数量。如果a_p的值较小,曲线的解就更多;反之,a_p的值较大,则解的数量更少。尽管计算曲线的秩相当复杂,但是找出a_p序列却容易得多。基于一台非常早期的计算机上计算出的成果,数学家Birch和Swinnerton-Dyer提出了一个猜想。他们认为,椭圆曲线的秩与a_p序列之间存在特定的关系。谁要是能证明他们的猜想是正确的,不仅能赢得一百万美元的奖金,还将在数学史上青史留名。
在2020年,英国皇家学会伦敦数学科学研究所的研究员Yang-Hui He(何杨辉),决定借助AI来挑战椭圆曲线问题。何教授本科学的是物理,然后在MIT取得了数学物理博士学位。但随着时间的推移,他对数论的兴趣与日俱增,并且开始考虑用AI来探索数字中的未知规律。此前,他就已经开始利用机器学习,对弦论中广泛使用的Calabi-Yau流形进行分类了。
论文地址:https://arxiv.org/abs/1812.02893在2020年8月,何杨辉在诺丁汉大学的一场在线讲座中,表达了自己对于用AI发现数学新知识的悲观看法。当时,他是这么说的:「我没有任何进展,因为我不是这一领域的专家。我甚至都没有找到正确的方法。」当时的听众之一、威斯敏斯特大学的数学家Thomas Oliver回忆道,他之所以认为数论很难,是因为无法简单地把机器学习应用在数论研究中。
由左至右:Kyu-Hwan Lee,Thomas Oliver,何杨辉后来,Thomas Oliver便叫上康涅狄格大学的数学家Kyu-Hwan Lee一同,与何杨辉展开了更深度的合作。「我们最初的目的,只是想了解一下机器学习是什么,而不是真的去深入研究数学,」Oliver说。「但很快,我们发现机器学习可以帮我们理解许多问题。」Oliver和Lee建议,大家可以用AI研究L函数,即通过序列a_p与椭圆曲线密切相关的无穷级数。为此,他们利用椭圆曲线及其相关L函数的在线数据库(LMFDB),训练了一个极其学习分类器。这个数据库收录了超过300万条有理数范围内的椭圆曲线及其相关的L函数。2020年10月,他们发表了一篇论文,通过分析L函数的信息,来预测椭圆曲线的特定性质。
论文地址:https://arxiv.org/abs/2010.0121311月,他们再次发表论文,利用机器学习对数论中其他对象进行了分类。
论文地址:https://arxiv.org/abs/2011.08958
论文地址:https://arxiv.org/abs/2012.04084但即便如此,三人都搞不明白,为什么机器学习算法会如此有效。
Lee把揭开这一谜团的任务,交给自己的本科生Alexey Pozdnyakov。
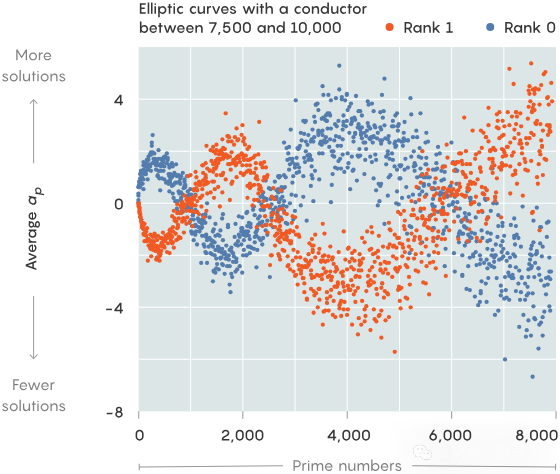
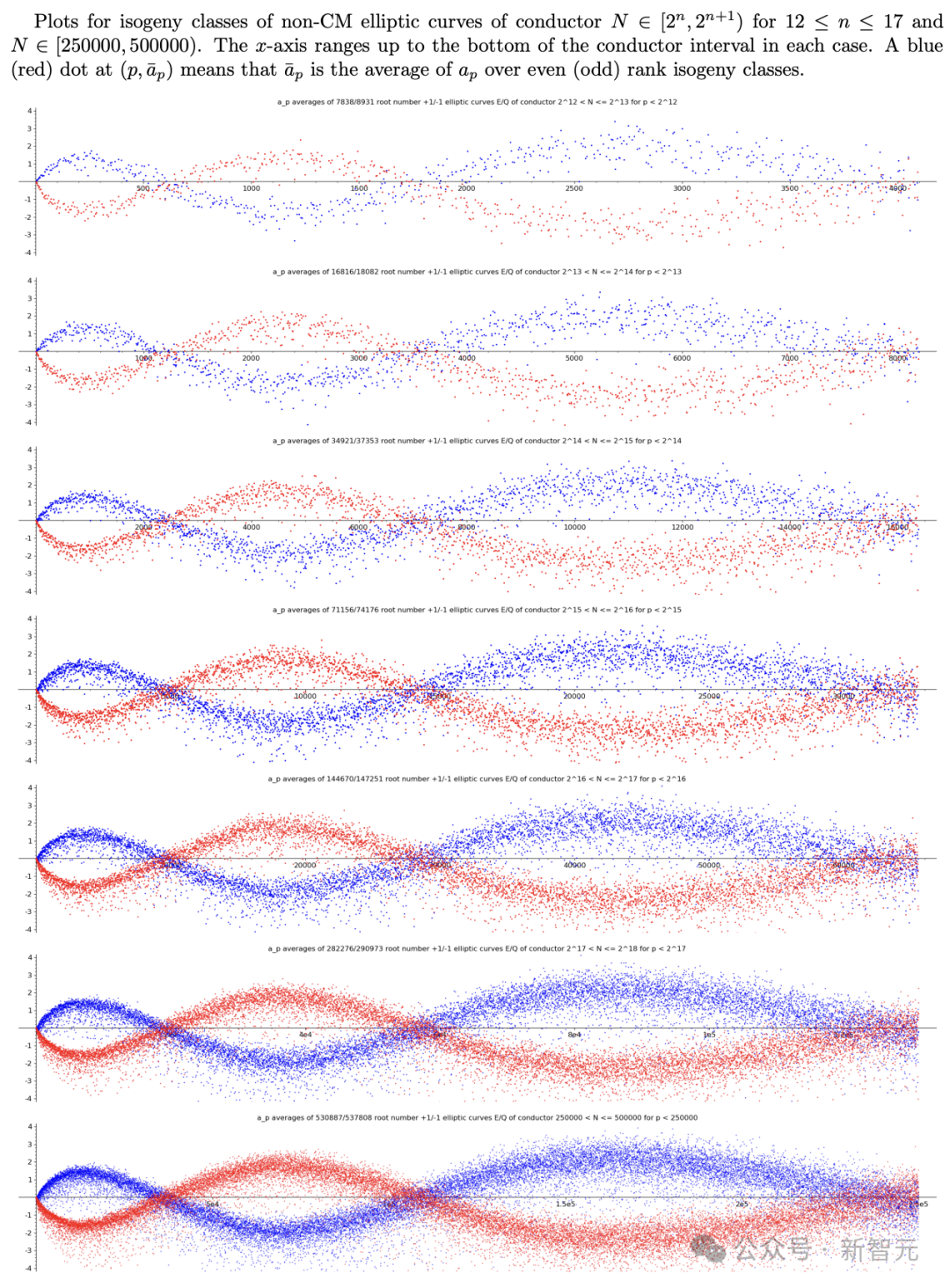
康涅狄格大学的本科生Alexey Pozdnyakov是世界上第一个观察到这种模式的人LMFDB通过一个叫做conductor的量,来对椭圆曲线进行分类,这个量概括了曲线在某些质数上表现不佳的信息。于是,Pozdnyakov尝试同时研究大量具有相似conductor值的曲线,比如conductor值为7,500到10,000之间的所有曲线。总的来说,这项研究涵盖了大约10,000条椭圆曲线。其中,有大约一半的秩为0,另一半的秩为1(更高秩的曲线极其罕见)。接着,Pozdnyakov分别计算了秩为0和秩为1的曲线的a_p值的平均数,并将这些数据绘制成图。结果显示,这两组数据形成了两个截然不同、清晰可辨的波。而这,就是机器学习能够准确预测特定曲线等级的原因。最初,Pozdnyakov只是很高兴自己完成了导师交代的任务。Kyu-Hwan教授立刻敏锐地意识到,这其中绝对有不寻常的发现!当Lee教授和Oliver教授知道后,他们也非常惊喜。Pozdnyakov向他们展示了上面的那张图,他们立刻联想到了鸟群在空中飞行时形成的图案。Kyu-Hwan教授随后查到,这种现象叫做murmuration。何教授随后提议,将论文命名为「椭圆曲线的murmuration」。
论文地址:https://arxiv.org/abs/2204.10140论文引起强烈反响
2022年4月,他们将论文上传,分享给一些数学家。大家忐忑地想,或许这个所谓的发现早就为人熟知,毕竟曲线实在太明显了。然而,出乎他们意料的是,论文一经发布,立刻引起了数学界的轰动。MIT科学家Andrew Sutherland对此尤为感兴趣。
作为LMFDB的管理编辑之一,Sutherland发现,原有的300万条椭圆曲线对于他的研究目标来说,是远远不够的。他希望通过研究更大范围的conductor,来检验所谓的「murmuration」是否具有普遍性。因此,他从另一个拥有约1.5亿条椭圆曲线的庞大数据库中提取了数据。但他对此仍然不满足,于是又从另一个包含3亿条椭圆曲线的数据库中再次提取数据。最后,Sutherland的数据集,包含了超过10亿的椭圆曲线。通过这个数据集,绘制出了非常高清的图像。他发现,无论是是15000条椭圆曲线,还是100万条,这种「murmuration」始终都会显现。更令人惊讶的是,即使在椭圆曲线涵盖的质数范围越来越大时,这种图形的形状依然保持不变,这种现象被称为「尺度不变性」。Sutherland还发现,这种「murmuration」不仅存在于椭圆曲线中,也会出现在更一般的L函数中。他将这些发现发送给了滑铁卢大学的Michael Rubinstein教授和Sarnak教授。他对此百思不得其解:「如果这背后有一个已知的原因,我相信你们一定能告诉我」。
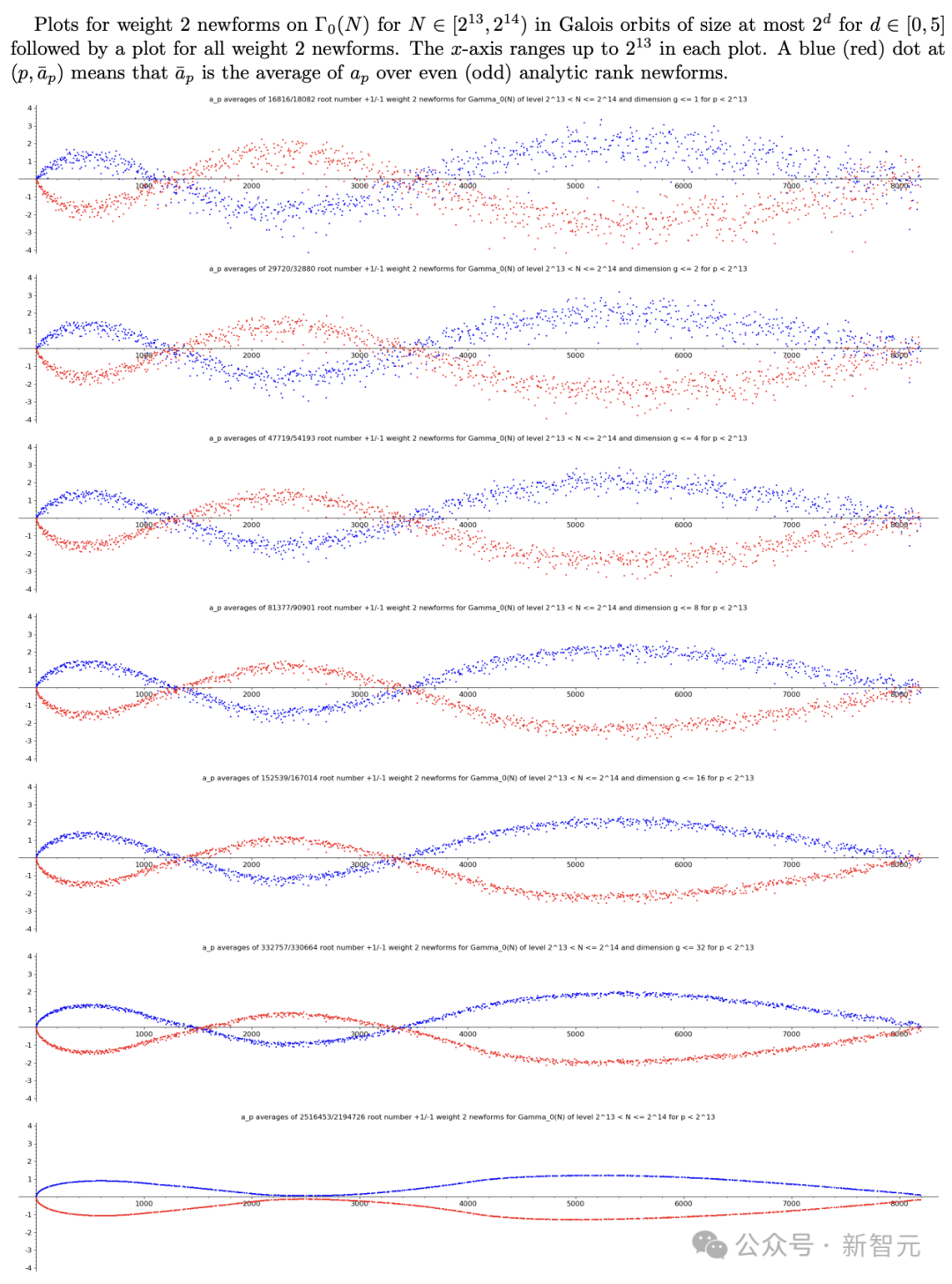
2023年8月,何杨辉、Lee和Oliver在布朗大学的计算与实验数学研究所(ICERM)举办了一场专门探讨murmuration的研讨会,并吸引了包括Sarnak和Rubinstein在内的众多学者参与。会上,Sarnak的学生Nina Zubrilina介绍了自己在模形式中,针对murmuration的研究成果。模形式是一种特殊的复函数,它们与椭圆曲线相似,都有对应的L函数。Zubrilina发现,在conductor较大的模形式中,murmuration呈现出一种趋向于集中成一条清晰的曲线,而非分散的模式。随后,她在2023年发表的一篇论文中,证明了这种murmuration遵循一个明确的公式。
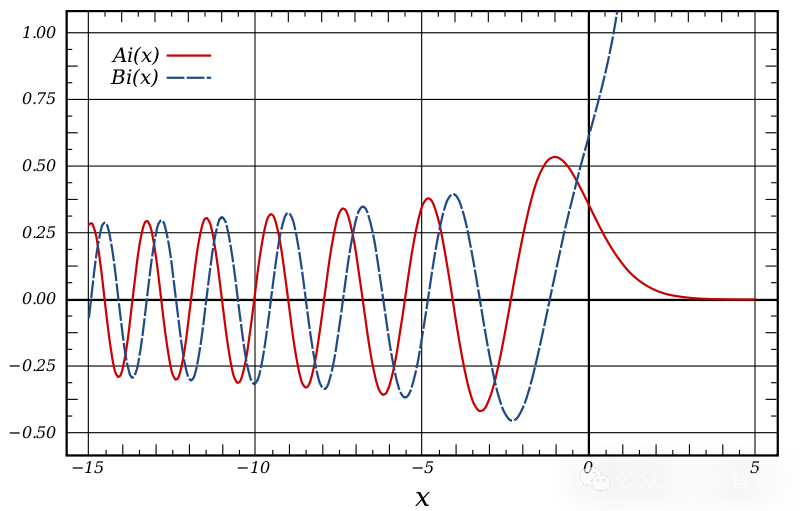
论文地址:https://arxiv.org/abs/2310.07681Sarnak对此评价道:「Nina的重大贡献在于她提出了一个『Zubrilina murmuration密度公式』。她运用了高深的数学知识,证明了一个与数据完美吻合的精确公式。」尽管这个公式相当复杂,但Sarnak认为它是一种重要的新型函数,甚至可以和定义微分方程解的艾里函数相媲美——后者定义了在物理学中各种情况下使用的微分方程的解,从光学到量子力学。而Zubrilina公式的提出,直接引爆了这个领域,现在几乎每周都有相关的新论文发布。Sarnak解释说,这些研究主要是采用Zubrilina的方法,进一步探讨murmuration的不同方面。Jonathan Bober、Andrew Booker和Min Lee来自布里斯托大学,他们与ICERM的David Lowry-Duda合作,在一篇10月份的论文中证明了模形式存在一种不同的murmuration。此外,Kyu-Hwan Lee、Oliver和Pozdnyakov还证明了在被称为狄利克雷特征的对象中存在murmuration,这些对象与L函数有着密切的联系。数学的重大发现,有很多「偶然」
如今回想起来,对于这一发现背后所需的重大运气,Sutherland仍然会不住感慨。如果当初,椭圆曲线的数据没有按照conductor来排序,那么murmuration可能就不会被发现。「他们很幸运地使用了LMFDB中已经按conductor预排序的数据,这是关联椭圆曲线和对应模形式的关键,但这并不是显而易见的……两个方程式看似相似的曲线,其conductor却可能大相径庭。」例如,方程y^2=x^3–11x+6的conductor是17,而将减号改为加号后,y^2=x^3+11x+6的conductor则为100,736。不仅如此,murmuration的发现,也在一定程度上多亏了本科生Pozdnyakov的经验不足。「如果没有他,我们可能不会发现这一点,」Oliver说,「因为专家通常会把a_p的绝对值归一化为1。但他没有这样做……因此,振荡才变得非常明显。」Oliver指出,AI算法用于按等级排序椭圆曲线的统计模式,存在于一个具有数百维的参数空间中——这对人类来说太复杂了,难以在脑海中排序,更不用说可视化了。虽然是机器学习首先发现了这些隐藏的振荡,但数学家们直到后来才明白,这些振荡实际上就是murmuration。
何杨辉是一位杰出的数学物理学家,目前是伦敦数学科学研究所的研究员,以及牛津大学默顿学院的导师。与此同时,何教授还在伦敦大学城市学院担任数学客座教授,在南开大学担任长江学着讲座教授,并且还是STEMM全球科学协会主席。何教授的研究工作横跨量子场理论、弦理论、代数几何和数论等多个领域,并深入探索AI和机器学习在这些问题中的应用,是利用AI进行纯数学研究的领域先驱之一。目前,何教授已发表超过200篇科学论文,并定期举行公开讲座。此外,他还积极参与科普活动,担任BMUCO顾问和One Garden研究员,致力于将科学知识普及给更广泛的公众。何杨辉在1975年9月出生于中国芜湖,在中国和澳大利亚度过了他的小学时光,随后在澳大利亚和加拿大完成了高中学业。1996年,何杨辉以最高荣誉(summa cum laude,同时获得Allen Shenstone奖和Kusaka Memorial奖)从普林斯顿大学获得物理学学士学位,并同时取得了应用数学和工程物理的双重证书。紧接着,他在1997年以优异的成绩从剑桥大学获得了硕士学位,并在2002年在麻省理工学院理论物理中心完成了他的博士学位研究(获得了美国国家科学基金会奖学金和麻省理工学院总统奖)。完成在宾夕法尼亚大学的博士后工作后,何杨辉加入牛津大学,担任FitzJames研究员和英国STFC高级研究员。https://www.quantamagazine.org/elliptic-curve-murmurations-found-with-ai-take-flight-20240305/
内容中包含的图片若涉及版权问题,请及时与我们联系删除

















































评论
沙发等你来抢