
机器学习的可解释性历来是学术界与工业界共同关注的重要议题。尽管目前许多关注都集中在最新机器学习模型的可解释性挑战上,然而,一些传统机器学习问题,如聚类问题,似乎同样存在一些可解释性方面的问题。
假设我们手头有
聚类问题,作为无监督机器学习领域的一个经典课题,虽然求取最优解是一个 NP-hard 问题,但随着技术的发展,我们已经拥有了许多高效的近似算法来得到近似最优解,比如广为人知的
然而,传统的
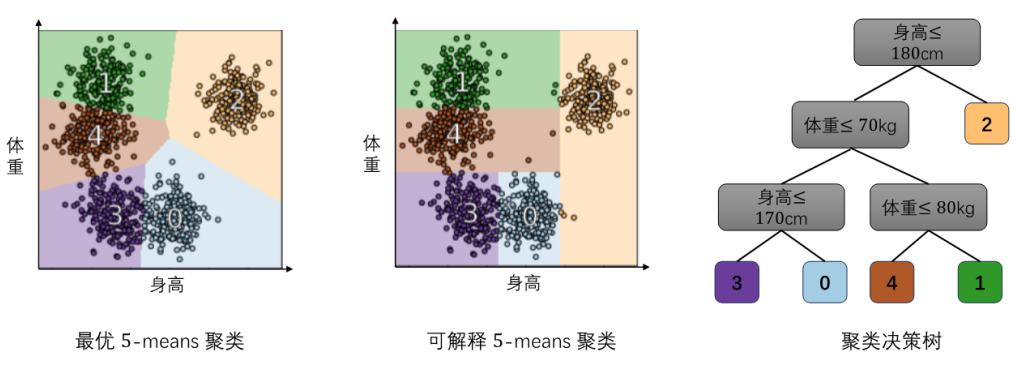
图1. 最优
为了解决这一问题,Moshkovitz 等人[2]提出了可解释聚类问题(Explainable Clustering),尝试利用决策树来构建聚类,从而大大提高了聚类的可解释性。以体型分类为例,我们可以考虑这样一种聚类方式:初始时,我们只有一个类,即整个数据集,然后选择一个特征维度(如身高)和一个合适的阈值
不过,我们自然会提出一个问题:这样的聚类方法其效果如何呢?Moshkovitz 等人[2]在提出可解释聚类问题的同时,也设计了一种构造可解释聚类的算法,其输出的聚类
随后,研究者们不断努力,试图改进聚类的可解释性代价的上下界。随着研究的深入,一个简洁而高效的算法被提出:在每次分割一个类时,我们只需随机选择一个特征维度和阈值即可。Gupta 等人[3]证明,这种随机分割策略可以将
聚类的可解释性代价概念自2020年被提出以来,便受到了计算机理论研究者们广泛的关注。在这里我们简要梳理了欧氏空间中
参考文献
[1] Arthur, David, and Sergei Vassilvitskii. "k-means++: The advantages of careful seeding." SODA. Vol. 7. 2007.
[2] Moshkovitz, Michal, et al. "Explainable k-means and k-medians clustering." ICML 2020: 7055-7065.
[3] Gupta, Anupam, et al. "The price of explainability for clustering." FOCS 2023: 1131-1148.
[4] Gamlath, Buddhima, et al. "Nearly-tight and oblivious algorithms for explainable clustering." NeurIPS 2021: 28929-28939.
[5] Makarychev, Konstantin, and Liren Shan. "Near-optimal algorithms for explainable k-medians and k-means." ICML 2021: 7358-7367.
[6] Bandyapadhyay, Sayan, et al. "How to find a good explanation for clustering?" Artificial Intelligence 322 (2023): 103948.

文 | 楼家宁
图 | 朱成轩

— 版权声明 —
本微信公众号所有内容,由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料,版权属北京大学前沿计算研究中心微信所有;从公开渠道收集、整理及授权转载的文字、图片和音视频资料,版权属原作者。本公众号内容原作者如不愿意在本号刊登内容,请及时通知本号,予以删除。

内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢