基础

1. 几何图

几何图G定义为G = (A, H, X)，其中A ∈ [0, 1]N×N是邻接矩阵，H ∈ R N×Ch是维度为Ch的节点特征矩阵，X ∈ R N×3 是所有节点的几何信息（3D坐标）。X 的形状从 N × 3 扩展到 N × 3 × C，其中 C 表示通道数。

在欧氏空间中，几何图通常表现出平移、旋转和反射的物理对称性，一般使用群来刻画这些变换，包括欧式群、平移群、正交群、置换群等等。直观上看，可以理解为置换、平移、旋转、翻转四种操作按一定顺序的复合。

2. 群（Group）

群表示（Group representation）：群的表示是可逆线性映射ρ ( g ) : G → V，g ∈ G是群中的元素，同时它是线性的：ρ ( g ) ρ ( h ) = ρ ( g ⋅ h ) , ∀ g , h ∈ G 

群表示可以理解为变换的表示。比如：

  • O(n) 表示旋转和反射组成的n nn维正交群
  • SO(n) 是一个只包含旋转的特殊正交群
  • E(n) 是由旋转、反射和平移组成的n nn维欧几里得群
  • SE(n) 是一个由旋转和平移组成的特殊的欧几里得群

3. 不变性与等变性

  • 不变性 (invraiant) ：对于一个函数，如果对其输入施加的某种操作丝毫不会影响到输出，即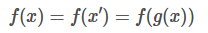：则称f对变换g具有不变性
  • 等变性 (equivariant)：对于一个函数，如果你对其输入施加的变换也会同样反应在输出上，即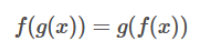：则称该对变换有等变性。

4. 不同模型的对称性

  • CNN具有平移不变性，网络可以对出现在图片中不同位置的同一物体做同样的分类；
  • RNN 具有时移不变性，输入序列整体前移或后移若干 token 并不会影响网络的输出；
  • GNN 则具有顺序不变性，不管一个节点的邻居以怎样的顺序输入网络，经过聚合函数得到的结果都是一样的。

5. WL Test (Weisfeiler-Lehman)

在大多数图上会得到一个独一无二的特征集合，这意味着图上的每一个节点都有着独一无二的角色定位（例外在于网格，链式结构等等）。因此，对于大多数非规则的图结构，得到的特征可以作为图是否同构的判别依据，也就是WL Test.

当我们要判断 Graph1 和 Graph2 是否同构时，WL test 的主要步骤如下图所示，通过聚合节点邻居的 label，然后通过 hash 函数得到节点新的 label，不断重复知道每个节点的 label 稳定不变。

稳定后，统计两张图的label的分布，如果分布相同，则一般认为两张图同构。

6. 归纳偏差or归纳偏置（inductive bias）

从现实生活中观察到的现象中归纳出一定的规则，然后对模型做一定的约束，从而可以起到"模型选择"的作用，即从假设空间中选择出更符合现实规则的模型（可以理解为一个正则化方式）。

几何深度学习

旨在寻找一种通用化的数据表示，并以此为基础设计模型，其核心是从对称性或者不变性出发，将几何性质嵌入到机器学习流程当中，更好地刻画数据的内在结构和变化规律，提高算法的表示、泛化、通用能力。

1. 几何图神经网络分类

  • 不变（invariant）模型
  • 等变（equivariant）模型，等变模型又细分为标量化方法模型（Scalarization-Based Model）与基于球面调和的高阶可操控模型（High-Degree Steerable Model）
  • 受 Transformer 架构启发的 Geometric Graph Transformer模型

(1) MP-GNN

单层的 GNN 通过message passing 和 feature update 两步操作得到一个输出。其中 message passing 以当前节点和任一邻居节点的特征作为输入，经过一个 MLP，得到该邻居的message；feature update 则是以节点当前特征和不同邻居 message 的聚合为输入，经过另一个 MLP，得到节点更新后的特征。可以看到，由于要经过两个不同的 MLP，其中包含了若干非线性变化，最终网络输出的节点特征更新是不满足旋转不变性或等变性的。

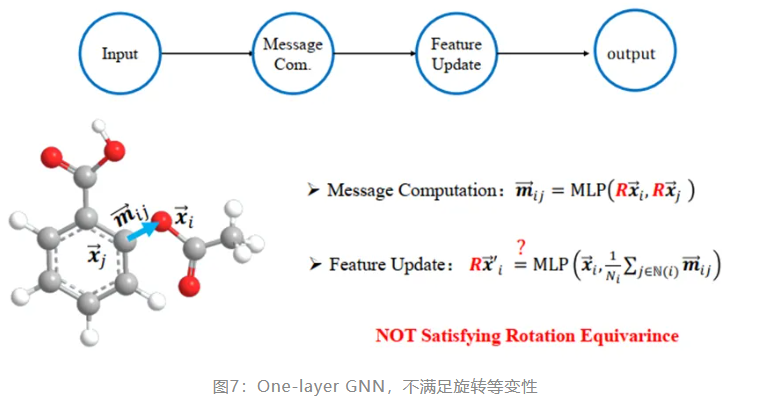
典型的 MPNN 架构由几个传播层组成，基于邻居特征的聚合函数对每个节点进行更新。根据聚合函数的不同，可以将 MPNN分为：

  • 卷积（邻居特征的线性组合，权值仅依赖于图的结构）
  • 注意力（线性组合，权值依赖于图结构和特征）
  • 和消息传递（广义的非线性函数）

(2) 不变GNN

在欧式空间中，长度和夹角是不会因为旋转而发生变化的。不变GNN就利用了这个几何性质，把原子的坐标替换为了相对距离、原子键长度和夹角，因此无论怎样变换坐标系，输入是不变的，输出也就是不变的。因此不变模型主要利用节点本身的特征与原子间的不变特征（距离、角度、二面角）等进行消息计算，随后进行传播。

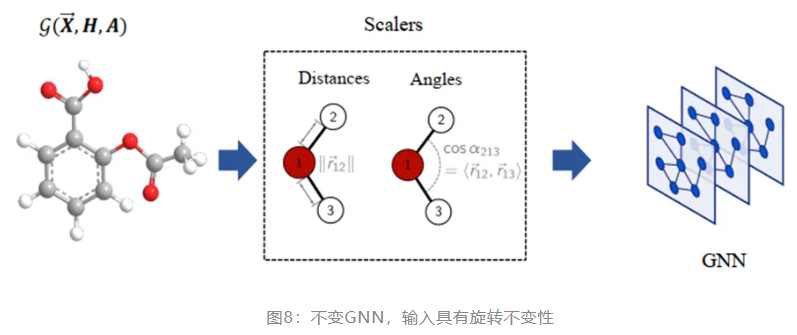
但这样的方法也存在一些缺陷，它只能描述局部的几何关系，丢失了全局子图间的相对位置关系。就像毕加索的画作，各五官被打乱又重新组合在脸上，看起来完全失真了。因此该缺陷也被称为毕加索问题（Picasso Problem）。 基于 WL-test 的图同构检测算法无法检测出此类区别，因此辨别能力与 WL-test 相当的GNN结构都会面临同样的问题。

(3) 等变 GNN

与仅进行不变特征更新的不变 GNN 相比，鉴于许多实际任务（例如分子动力学模拟）需要等变输出，等变 GNN 同时更新不变特征和等变特征。更重要的是，等变 GNN 比不变 GNN 更具有表达能力，特别是对于稀疏几何图。

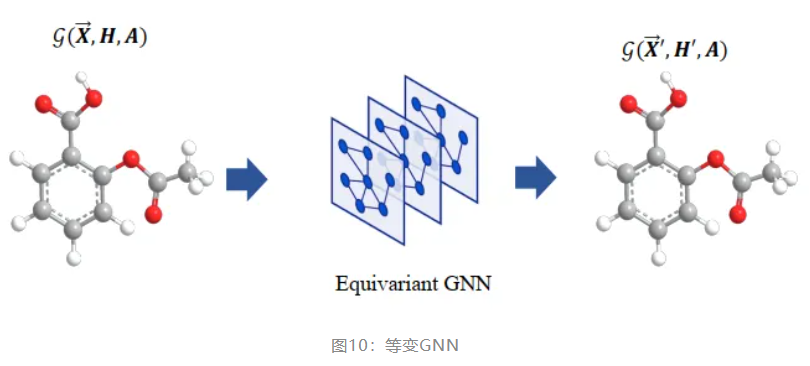
等变 GNN 则在每一层网络中都保留了节点的坐标信息，能很好地解决以上问题。计算每一层的输出时，等变 GNN 也进行了特别设计。首先，用相对坐标代替绝对坐标，满足了平移不变性；其次，在进行 message passing 时，以内积为输入，满足了旋转不变性，于是最终的输出满足了旋转等变性。

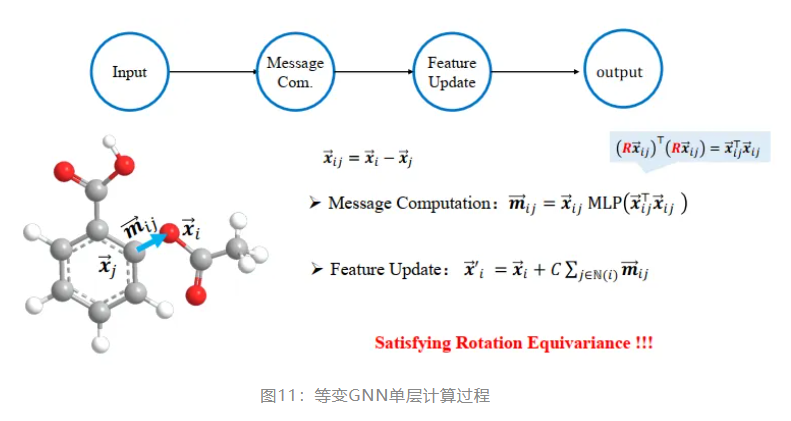
  1. 标量化方法模型：标量化方法额外通过节点间坐标差引入了几何信息，并将不变信息作为几何信息的权重进行线性组合，实现了等变性的引入。
  2. 高阶可操控模型：则是使用了高阶的球谐函数（Spherical Harmonics）与维格纳-D ( Wigner-D ) 矩阵表征系统的几何信息，并通过Clebsch–Gordan 系数操控不可约表示的阶数，从而实现几何消息传递过程。
    • Wigner-D 矩阵，将 3D 旋转转换为不同阶数的群表示；
    • 球谐函数是单位球面 S 2 上的一组傅里叶基，将3D向量转换为不同类型的可操纵特征；
    • Clebsch-Gordan (CG) 张量积 ，用于在可操纵特征之间执行等变映射。

 

参考连接

几何深度学习：让物理世界拥有AI | 黄文炳分享整理 (qq.com)

AI4Science的基石：几何图神经网络，最全综述来了！ - 智源社区 (baai.ac.cn)

 

内容中包含的图片若涉及版权问题，请及时与我们联系删除