芒种 | 拍卖机制设计中的不可能三角

拍卖（Auction）是人类社会一种古老的商品交易形式，最早可以追溯到公元前500年。通常而言，拍卖是一种买卖商品或服务的过程，即通过提供竞标、接受竞标，然后将商品卖给出价最高的人。随着商业和经济的发展，拍卖机制设计（Auction Mechanism Design）成为拍卖理论中愈发重要的研究领域。它研究的是如何制定分配规则来决定哪位参与者可以获得物品，以及如何制定计费规则来决定向参与者收取多少费用。不同的机制设计不仅会影响到交易结果，还会影响到参与者的行为策略。

我们通常希望设计出的拍卖机制具有一些良好的性质，例如激励兼容（Incentive-Compatibility）。激励兼容是指无论其他人报什么样的价格，出价自己对物品的真实估价可以带来最高的期望收益。满足激励兼容性质的拍卖机制被称为防策略（Strategy-Proof）机制。

一种经典的防策略拍卖机制是密封二价拍卖（Sealed-Bid Second-Price Auction），又称维克里拍卖（Vickrey Auction）^[1]：参与者在不知道其他人出价的情况下出价，出价最高的人获得物品，但只需付次高的出价。如果出价最高的人需要支付的费用变为自己的出价，则拍卖机制就变为密封一价拍卖（Sealed-Bid First-Price Auction），而密封一价拍卖不满足激励兼容的性质。

另一种经典的防策略拍卖机制是公开升价拍卖（Open Ascending-Price Auction），又称英式拍卖（English Auction）：从起点价格开始，参与者逐一叫价，叫价以公开方式进行，一直持续到无人再加为止，出价最高者赢得拍卖并支付自己的报价。英式拍卖是非静态的（Non-static），这意味着拍卖流程只能异步进行，相比于静态的（Static）密封拍卖而言效率差很多，会更难适应要求实时拍卖的场景，例如互联网搜索广告。

传统机制设计范式往往假设卖家诚信地遵循他在拍卖开始前声明的拍卖规则，即便观察到所有参与者的报价后发现有利可图，也不会失信。我们不禁会想，既然要求激励兼容的性质是在考虑买家的策略性行为，为什么不考虑卖家的策略性行为呢？卖家不是也有可能作弊吗？

不难发现，卖家想在密封二价拍卖中作弊很容易。由于每位出价者都看不到其他人的报价，那么卖家完全可以虚报一个次高价。例如，卖家可以向出价100元并获得物品的参与者收取99.99元，哪怕真正的次高价只有1元，卖家也只需要声称次高价是99.99元——毕竟这确实有可能。已有一些实验性工作发现卖家在密封二价拍卖中诚信度确实会越来越低^[2]，还有一些理论性工作研究在允许卖家作弊的拍卖规则下双方博弈情况如何 ^[3,4]。

尽管根据传统分析框架，英式拍卖与密封二价拍卖具有几乎相同的交易结果，英式拍卖却不存在卖家可能作弊的问题。如果参与者是通过出价100元获胜的，那么他就会支付100元，卖家无法操纵收费，更不愿提前结束叫价流程。同样的，密封一价拍卖中卖家也不会作弊。

因此，卖家是否有机会作弊实际上是评价拍卖机制的另一个重要维度。如果一个拍卖机制能抑制卖家作弊，我们就称它是可靠的（Credible）。

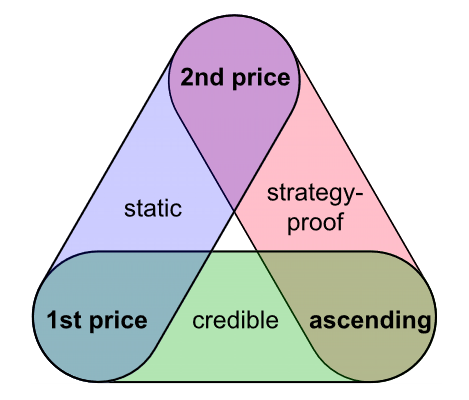
同时考虑上文提到的三条性质，实际上存在一个不可能三角^[5]。一价拍卖是静态的、可靠的，但它不是防策略的；二价拍卖是静态的、防策略的，但它不是可靠的；升价拍卖是可靠的、防策略的，但它不是静态的。

此外，还存在许多拍卖机制能够满足三条性质中的两条。虚拟二价拍卖（Virtual Second-Price Auction），又称梅尔森拍卖（Myerson Auction）^[6]，是静态防策略拍卖，而且它令卖家收入最优。可以类似地定义虚拟升价拍卖，它是最优的可靠防策略拍卖。在引入一些温和的假设后，包括全支付拍卖（All-Pay Auction）在内的一系列双报价拍卖（Twin-Bid Auction）都是静态可靠拍卖。

对不可能三角的研究和刻画可以帮助我们更深入地理解拍卖机制设计，在实践中通过权衡不同的目标设计出更为合适的拍卖机制。一个合适的拍卖机制有助于增加市场的透明度和稳定性，并能促进资源的有效配置和经济的健康发展。