卷友们好，我是rumor。

Batch size放大后，对应放大学习率是一个约定俗成的规律，但随着现在模型尺寸、计算量的增大、不同优化器的研发，这个结论是否仍然成立仍有待探究。近期腾讯的一篇工作就得到了不一样的结论。下面有请一作李帅朋为大家分享他们的发现～

平时工作学习中，训练模型时候比较重要的两个超参数是Batch size和Learning rate。在采用不同Batch size训练时候，该如何调整学习率？不同的优化器上Batch size对最佳学习率的选择是否有影响？

为了回答上面的问题，我们过往的研究做了一些调研：

2014年Alex在自己的“笔记”（https://arxiv.org/pdf/1404.5997）中记录过这样一段话：

Theory suggests that when multiplying the batch size by k, one should multiply the learning rate by sqrt(k) to keep the variance in the gradient expectation constant.

但是2018 年的一份工作（https://arxiv.org/pdf/1706.02677）中指出：

To tackle this unusually large minibatch size, we employ a simple and hyper-parameter-free linear scaling rule to adjust the learning rate. While this guideline is found in earlier work [21, 4], its empirical limits are not well understood and informally we have found that it is not widely known to the research community.

Alex提到的理论似乎失传了，并且他们发现可能直接采用随着Batch size的线性放缩更合适。

就在学习率放缩率这样反复横跳的时候，2018年年底OpenAI Scaling law的序章之一（https://arxiv.org/pdf/1812.06162）中对采用SGD进行Large-Batch训练的模型行为进行了系统的理论阐述和实验验证。其中一个比较重要的结论是，SGD 优化的模型其Batch size和Learning rate的放缩率服从：

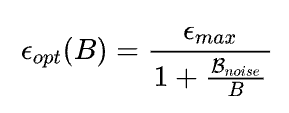
其放缩行为如下图所示：

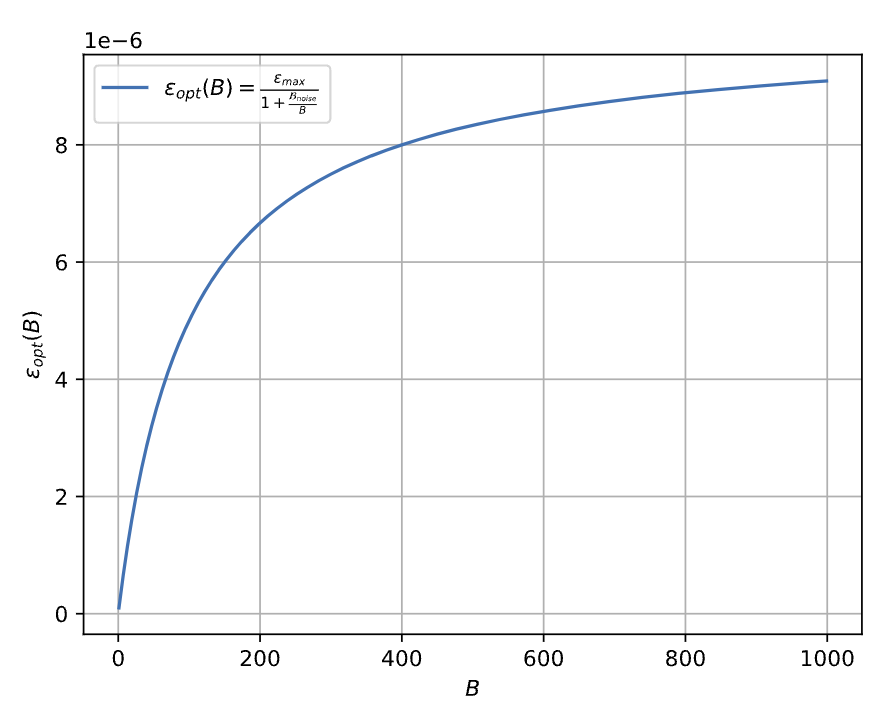
在Batch size较小的时候，学习率确实是近似与Batch size线性放缩的。但是随着Batch size变得更大，最优的学习率逐渐趋于饱和。那么有了上述理论结果是否意味着，Batch size和Learning rate 放缩关系这个问题已经彻底解决了？似乎OpenAI文章中的一段小字预示了结论：

One might also use preconditioned gradients, obtained for example by dividing gradient components by the square root of the Adam optimizer’s [KB14] accumulated variances. We experimented with this but found mixed results.

Emm...，好像Adam在实验现象和理论结论上有一些偏差，结果好坏参半。

1. 理论发现

最近我们的工作（Surge Phenomenon in Optimal Learning Rate and Batch Size Scaling）中，对Adam的情况进行了Review。Adam采用了形如

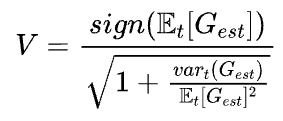
的更新方式（更多细节参考原文附录A）。当step方向的方差很小时可以简化为：

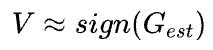
并且还发现OpenAI可能混淆了一个符号的含义：

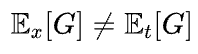
也就是说在推导过程中，沿着数据分布对梯度进行期望估计和沿着训练step方向对梯度进行期望估计是不等价的。在修正了这一推导过程中的问题后，他们得出Adam风格优化器在Batch size和Learning rate上的放缩率：

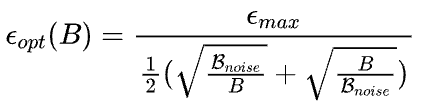
这样的结论如下图所示，与SGD有很大区别：

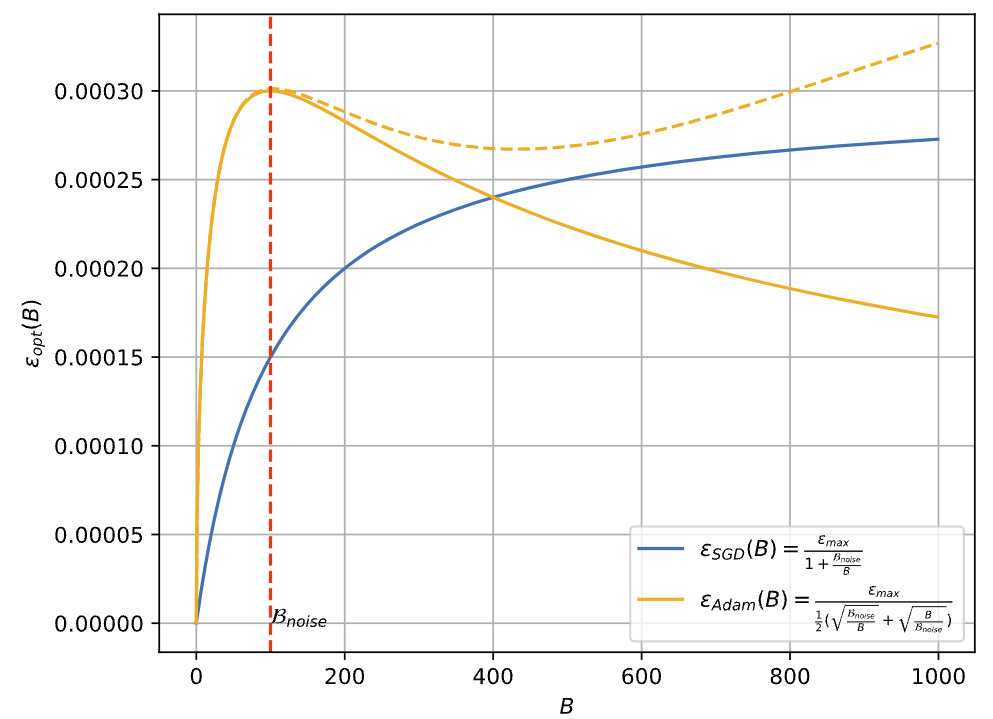
• 【结论1】放缩率的函数形状居然像一朵“浪花”一样
• 【结论2】难道Batch size增大，Learning rate需要降低？

既然理论推测使用Adam优化器时Batch size超过B_noise就会导致最优Learning rate下降，那么只要确定B_noise取值，然后在通过网格搜索打点观察就可以了。虽然直接对B_noise进行计算和统计很困难，但是OpenAI关于训练时间和样本效率关系的研究中我们可以估算出

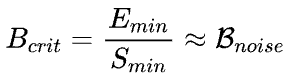
的取值（更详细的讨论参考原文中的附录G）。

并且根据函数公式不难发现在Batch size等于B_noise时候学习率达到波峰，而根据OpenAI 2020年的研究（https://arxiv.org/pdf/2001.08361）结论，B_noise随着训练服从一个与Loss相关的Scaling law：

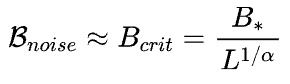
这就是说：

• 【结论3】随着训练进行，“浪尖”形状的放缩率图像会涌向大Batch size的方向

2. 验证理论

通过网格搜索可以观察到不同Batch size和Learning rate配置下Loss下降的快慢（下图中颜色越红，下降越快），如果理论正确的话，利用理论公式推算的Scaling law曲线应该可以尽可能的穿过图中红色区域：

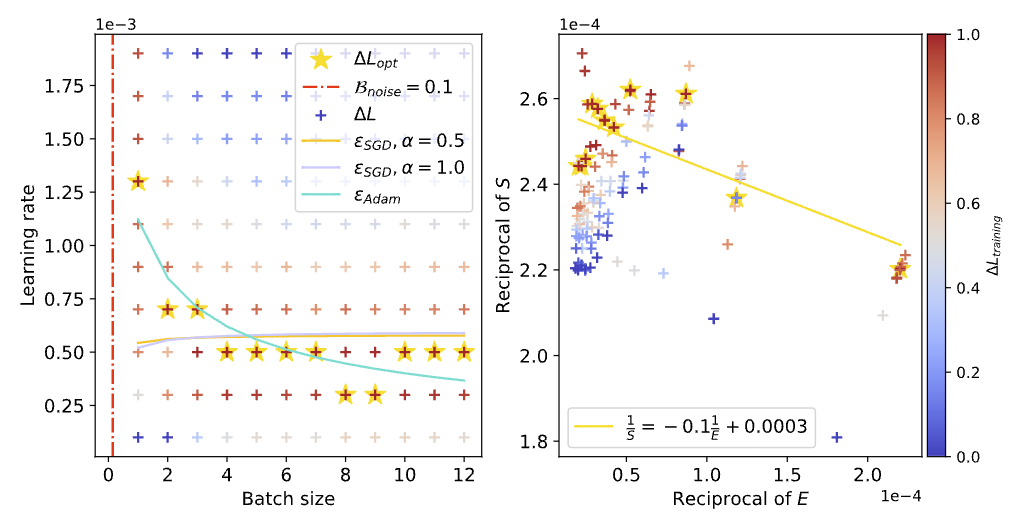
可以看到，上图中使用我们理论公式推算的青色Scaling law曲线，相比原始基于SGD推算的曲线（）能更准确的刻画红色区域的变化趋势，并且可以很明显观察到随着Batch size增加，反而需要降低Learning rate的现象。（更多实验参考原文Section 3）

3. 观测「浪涌现象」

使用和上一节相同方式，画出训练过程中不同Loss水平的Scaling law曲线，并观察「浪尖」的变化：

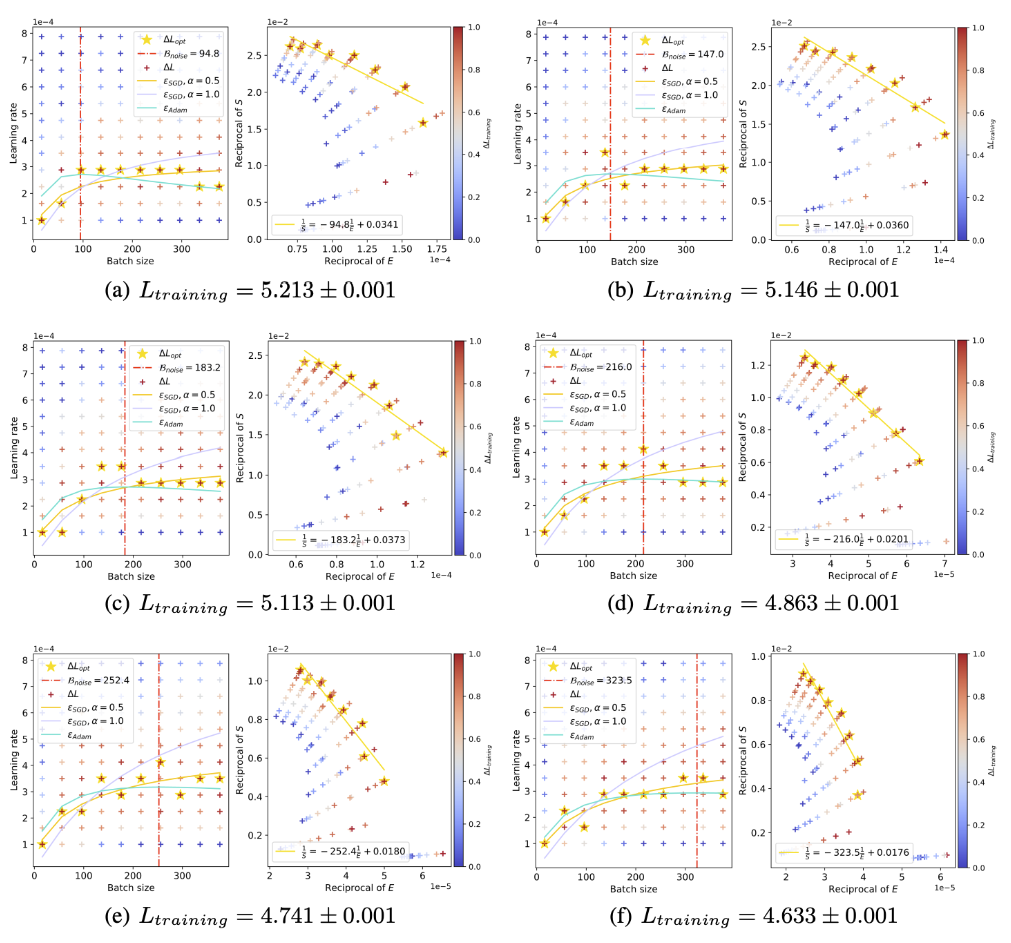
可以看到，随着训练Loss的降低，「浪尖」确实在逐渐向右也就是更大Batch size的方向移动。

4.额外的想法

理论和实验工作做到这里已经基本能回答文章最开始的问题了，但是这里仍然遗留了一些未来可以继续探索的东西：

1. 结论中的公式里除了以外，还有一个重要参数：

• 该如何快速估计？
• 能都将估计的方法集成到优化器里面？

2. 推导过程中参数的每个元素是独立，这也就以为了每个参数实际是有自己独立的Scaling law：

• 是否有必要每个参数都独立估计自己的和？
• 模型不同层之间的Scaling law是否也有关联性，能否也用一条或几条理论公式进行刻画？
• 稀疏模型相比稠密模型在Scaling时是否应该增加一个修正项？