EC 2024 | 基础比率谬误在预测聚合中的意外价值

关键词：信息聚合，基础比率谬误

导读

本文介绍了发表在 ACM EC 2024 的论文 The Surprising Benefits of Base Rate Neglect in Robust Aggregation。该论文由北京大学助理教授孔雨晴博士、北京大学计算机学院博士生王颖与清华大学经济管理学院经济系博士生王澍合作完成。文章揭示了一种特殊的“非理性”行为在鲁棒信息聚合中的意外价值。

论文链接：

https://arxiv.org/abs/2406.13490

现场交流：Great Hall & Hall B1+B2 (level 1) #1713

Room 2420, Yale School of Management, New Haven

Thursday, July 11, 10:30-11:30 (ET)

引入

你正在考虑投资一个名叫 NeuroLink AI 的脑机接口项目。

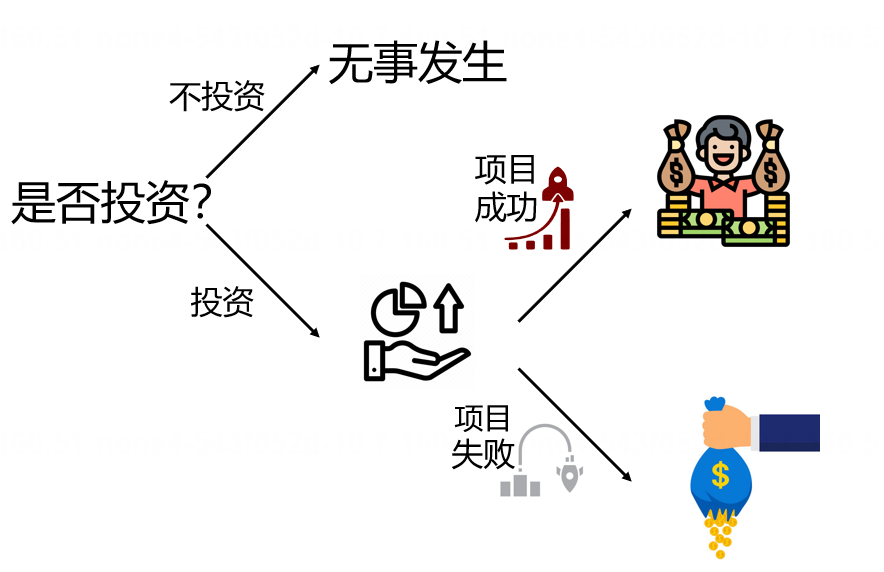
图1. 投资决策问题

可是，投资获利是一件很难的事：能够成功并且带来回报的项目仅仅占创业项目的很小一部分。如果项目失败，你的所有投入都会打水漂。

你知道，投资 NeuroLink AI 是否能获利取决于这个项目成功的概率。然而，身为外行的你对脑机接口的技术原理和市场前景一无所知。你也没有任何可靠的秘密情报。于是，你只能去选择咨询专家。

图2. 咨询专家

你决定询问一个技术专家和一个市场专家。不过，专家只能告诉你“他认为这个项目有多少几率会成功”。

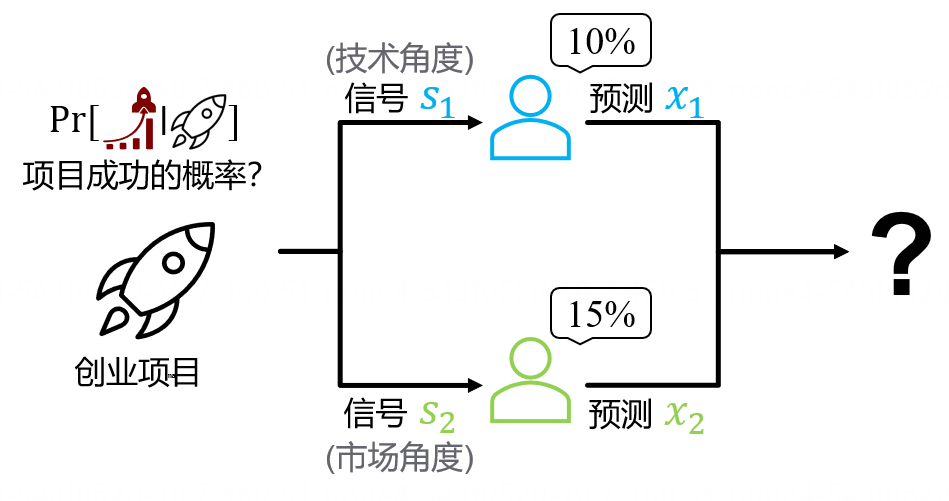
图3. 预测聚合

令人头疼的是，一个项目在不同方面的表现可以大相径庭（项目可以同时拥有领先同行的技术和非常糟糕的市场规划，也可能拥有平平无奇的技术和天才般的营销策略）。另一方面，即使从同一视角进行评估，不同的技术专家也可能给出不同的预测。因此，通常情况下，专家们的预测不完全一致。你还需要综合不同专家的预测意见，给出一个聚合预测。

【专家选择问题】明天就是脑机接口创业大会，你可以选择去人类分会场询问行业大佬，也可以选择去机器人分会场询问机器人专家。为了得到尽可能精确的聚合预测，你应该询问哪组专家？

图4. 专家选择问题

点击空白处揭晓答案

【答案揭晓】令人意外的是，我们的研究表明，咨询会犯错的人类专家可以得到更精确的聚合预测。

基础比率谬误：一种特殊的“非理性”推理模式

相比于机器专家，人类专家更容易出现“非理性”的推理模式。特别地，我们关注一种名为基础比率谬误的预测行为。

在给出正式的定义之前，让我们先看一个示例。

【示例】马克的脑机接口公司拥有前卫的产品理念，公司的初代产品也得到了市场用户的广泛认可。你觉得马克的公司能成功上市吗？

前卫的产品理念、广泛的用户认可度......这些都是积极的信号。你的直觉告诉你，马克的公司前景光明，公司一定能上市。然而，这种判断忽略了上市公司占比要远低于上市失败企业占比的统计数据。

这就是基础比率谬误（Base Rate Fallacy）。这种现象也叫基础比率忽视（Base Rate Neglect），它是普遍观察到的，人们被特征信息分散注意力而忽视相关统计信息的倾向^[1]。人们在做预测时常常只关注特征信息、忽略事件的基础比率，从而造成的预测失误。

回到项目投资的例子中，这次我们从专家的视角出发，理解专家是如何进行预测的。

专家视角

想象你是一个技术专家，你知道只有15%的创业项目会成功。按照技术划分，80%的成功项目采用先进技术，而80%的失败项目采用普通技术。

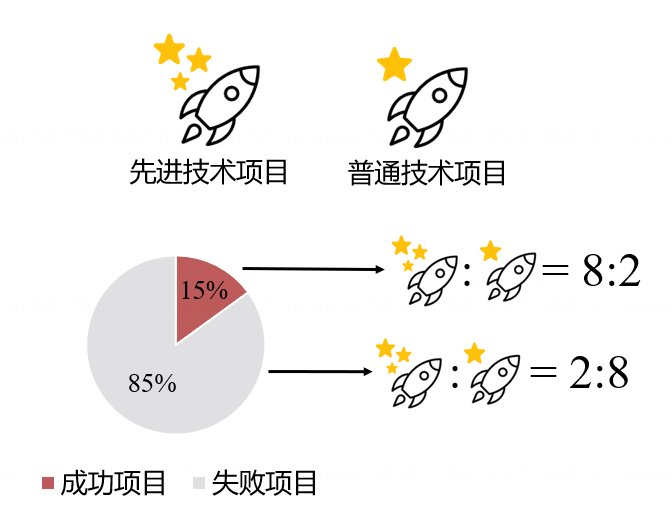
图5. 信息结构（专家视角可见）

你考察发现 NeuroLink AI 项目采用的是先进技术，那么这个先进技术项目成功的概率是多少？

你的直觉可能会告诉你，答案是80%或63%^[#1]，但经过计算，你会发现正确答案是41%。

[#1] 另一类直觉回答是15%（即例子中项目成功的基础比率），它对应另一种预测失误——信号忽略（Signal Neglect）。

图6. 专家预测

预测分析

根据贝叶斯原则，一个先进技术项目成功的概率为 $\frac{15\%\times0.8}{15\%\times0.8+85\%\times 0.2} \approx 41\%$ 。

你的直觉回答80%可能是因为大脑忽略了项目成功的基础比率： $\frac{0.8}{0.8+0.2} = 80\%$ 。

如果你的直觉回答在41%和80%之间，那么你的大脑在给出预测时部分考虑了基础比率。

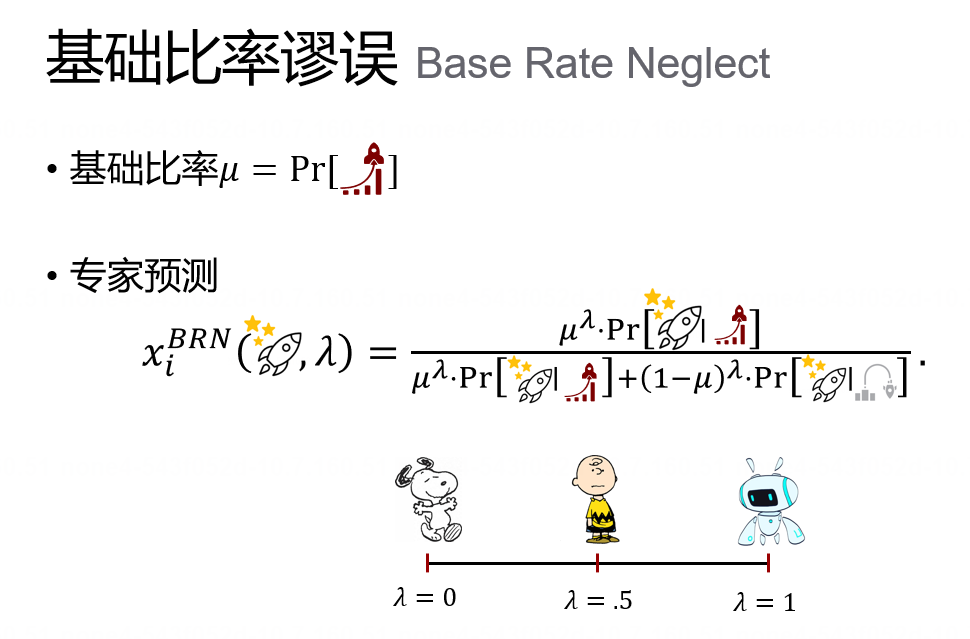
这就是人类预测中的基础比率谬误。根据文献^[2]，基础比率谬误下的专家预测 $x_i$ 可以表示为 $x^{BRN}_i(s_i, \lambda) = \frac{\mu^{\lambda}\cdot \Pr[S_i = s_i\mid \omega = 1]}{\mu^{\lambda}\cdot \Pr[S_i = s_i\mid \omega = 1]+(1-\mu)^{\lambda}\cdot \Pr[S_i = s_i\mid \omega = 0]}.$ 其中， $s_i$ 为专家 $i$ 观测到的信号，对应于例子中的先进技术信号， $\omega = 1/0$ 分别对应项目成功/项目失败。参数 $\lambda\in [0,1]$ 对应专家在做预测时考虑基础比率的程度：当 $\lambda=0$ 时，专家完全忽视基础比率，在预测中只考虑条件概率；当 $\lambda = 1$ 时，专家就是完美贝叶斯专家，按照贝叶斯原则得到完美贝叶斯后验。

图7. 基础比率谬误

专家选择问题的答案（正式描述）

我们假设人类专家以基础比率考虑程度 $\lambda =0.5$ 的进行预测，机器人专家则完美掌握贝叶斯原则（对应 $\lambda=1$ ），那么询问人类专家能够产生更准确的聚合预测。

理论分析与数值模拟

注意到聚合预测不仅和专家有关，还和聚合专家预测 $x_1, x_2$ 的方法有关。我们把聚合方法形式化为一个聚合函数或称聚合器（aggregator） $f:[0,1]\times[0,1] \to [0,1]$ ， $f$ 输入 $x_1,x_2$ ，输出最后的聚合预测 $f(x_1, x_2) \in [0,1]$ 。

考虑到作为投资人的你对信息结构（包括项目成功的基础比率、专家信号、信号与项目成功之间的联合分布这些信息）并不了解。为了评估聚合准确性，我们引入 Arieli, Babichenko, and Smorodinsky 在文献中提出的鲁棒框架^[3]。

【定义】当专家的基础比率考虑程度为 $\lambda$ 时，聚合器 $f$ 的 Regret（记作 $R_\lambda(f)$ ）为聚合预测 $f(x_1, x_2)$ 和全知聚合器 $f^*(\vec{s})$ 在最坏情况下的误差差距。

$R_\lambda (f)=\sup_{\theta\in\Theta} \mathbb{E} _\theta [L(f(\vec{x}(\vec{s},\lambda)))-L(f^∗ (\vec{s}))].$ 其中， $\Theta$ 是所有可能的信息结构构成的集合，这里我们对信息结构的唯一假设为两个专家的信号 $s_1, s_2$ 条件独立，即在已知 $\omega$ 的条件下 $s_1,s_2$ 独立； $L(y)$ 是聚合预测 $y$ 和实际结果 $\omega$ 之间的误差； $f^*(\vec{s})=\Pr_\theta[\omega = 1 \mid \vec{s}]$ 可以看成一个知道完整信息结构和所有专家信号的全知者给出的完美贝叶斯后验预测。在我们的例子中，这个全知者就是一个既懂技术又懂市场的全能型专家，他可以根据两方面的信号和基础比率利用贝叶斯原则计算出已知所有信息情况下完美的贝叶斯后验。

理论结果

我们的主定理表明，对任何聚合函数 $f$ ，当专家的基础比率考虑程度 $\lambda$ 从0增大到1时， $R_\lambda (f)$ 是单谷的（要么单调，要么先减后增）。

数值结果

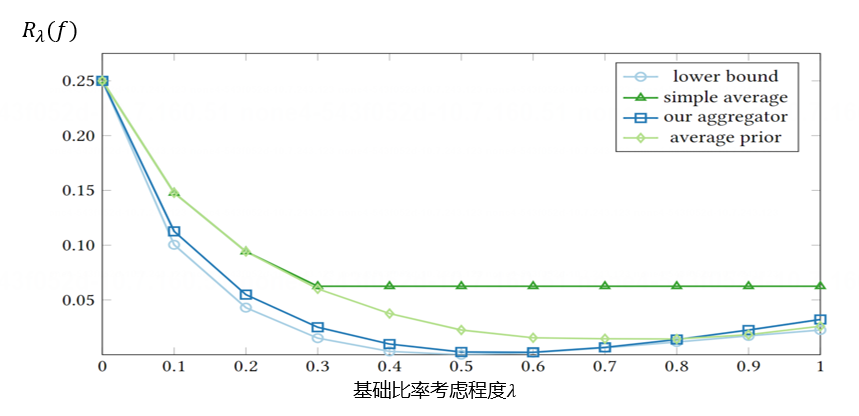
特别地，通过数值模拟，我们发现很多聚合器的 Regret 关于 $\lambda$ 不单调。这进一步说明这些聚合器的 Regret 在 $\lambda \in [0,1]$ 上构成一个 V 型（先单调减，再单调增）：即存在 $\lambda < 1$ 使得 $R_\lambda(f)<R_1(f)$ 。这意味着咨询两个存在基础比率谬误的专家可能比咨询两个贝叶斯专家得到更精准的聚合预测。

图8. 聚合器 Regret 与下界比较

此外，我们提出一组聚合器（如图8，our aggregator 曲线），其在 $\lambda=0.5$ 时的 Regret 接近于0。这意味着当专家的基础比率考虑程度 $\lambda =0.5$ 时，这组聚合器可以几乎精确地恢复全知者的后验概率。这个值远小于 $\lambda=1$ 时的 Regret 下界（如图8，lower bound 曲线），这说明使用我们提出的聚合器聚合两个 $\lambda = 0.5$ 的专家预测得到的结果比用任何聚合器聚合两个贝叶斯（ $\lambda=1$ ）专家预测都更准确。

实证分析

我们的实证研究使用标准的信念更新任务^[4][5]来提取被试的预测。在实验中，被试会看到两个箱子，每个箱子中有一定比例的红球和蓝球（两个箱子中的红球比例分别表示为 $p_{le}$ 和 $p_{ri}$ ）。每轮任务首先随机选中一个箱子（以 $\mu$ 的概率选中左边箱子，以 $1-\mu$ 的概率选中右边箱子），然后在选中的箱子中随机抽出一个球，球的颜色（红色/蓝色）将作为信号发送给被试^[#2]，被试在收到信号后需要估计抽中的球来自左边箱子的概率。

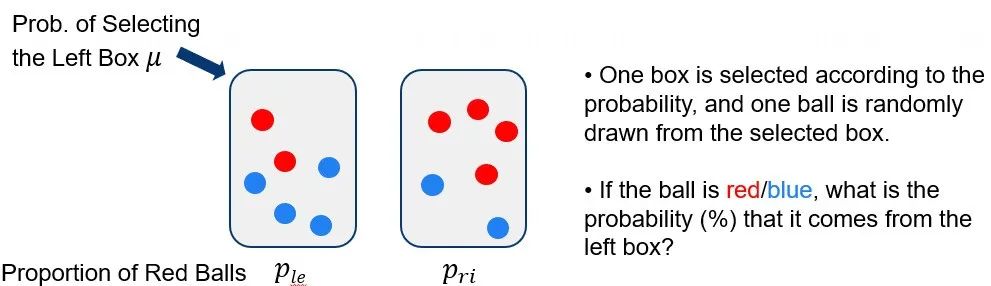
[2] 为了完整提取被试的预测策略，我们将询问被试“如果球是红色...”和“如果球是蓝色...”时的预测。每个被试需要回答30个随机生成的上述情境（对应一个 $\mu,p_{le}, p_{ri}$ 的组合），每个情境引出两轮任务（分别对应球是红色/蓝色），总共60轮。

图9. 任务设计

识别基础比率忽略现象

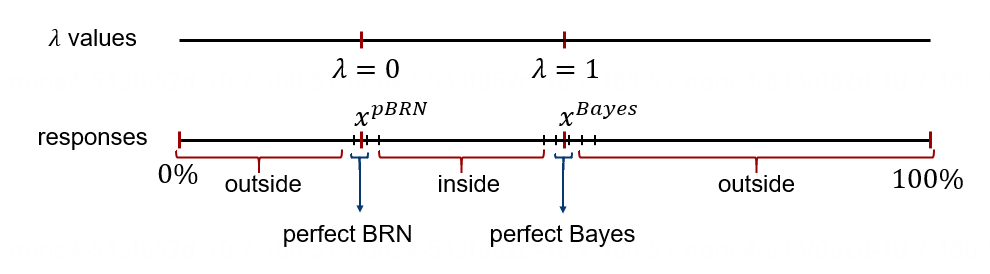
针对每个被试的每一轮任务，我们将回答划分为4类（perfect BRN, perfect Bayes, inside, outside）。其中 perfect BRN 对应 $\lambda=0$ 时的回答，即完全忽略基础比率的专家的后验预测；perfect Bayes 对应 $\lambda = 1$ 时的回答，即贝叶斯专家的完美贝叶斯后验预测；inside 对应 perfect BRN 和 perfect Bayes 之间的回答，这类回答部分考虑了基础比率；outside 对应其他回答，这类回答不符合理论模型的假设。

图10. 被试回答分类

分析被试的回答，我们发现四类回答有相对稳定的占比，这种占比在不同任务轮次之间和不同信号之间表现相对稳定。其中，outside 回答超过半数。

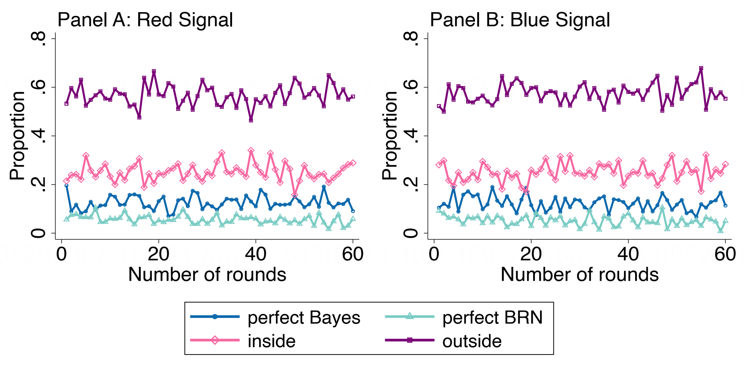
图11. 不同类型的被试回答比例

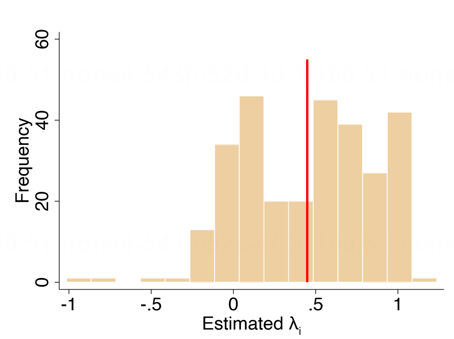
从被试个体层面分析，我们使用普通最小二乘回归（Ordinary Least Squares）得到每个被试的 $\lambda_i$ 值，发现人群的 $\lambda_i$ 表现出异质性。大部分被试的基础比率考虑程度 $\lambda_i$ 落在 $[0,1]$ 区间。特别的，如果直接回归人群的 $\lambda$ 值，得到人群的基础比率考虑程度 $\lambda$ （如图12红线所示）很接近0.5。

图12. 个体被试基础比率考虑程度分布图

不同聚合器的性能测评

我们测试我们提出的聚合器( $\hat{\lambda}$ -base rate balancing aggregator, $f^{\hat{\lambda}}_{ap}$ )和现有聚合器（包括 average prior 聚合器 $f_{ap}$ 和 simple average 聚合器 $f_{ave}$ ）在实验数据上的表现。发现在全样本上，simple average 聚合器 $f_{ave}(x_1,x_2) = \frac{x_1+x_2}{2}$ 的表现优于其他聚合器。

图13. 全样本分析：聚合器在被试预测上的表现

进一步观察聚合器在不同子样本^[#3]上的表现，我们发现：

当专家表现出基础比率谬误时（如图14，4 insde、4 perfect BRN、3 inside + 1 outside 子样本），我们的聚合器有更好的聚合准确性（更小的 Regret）。
对单个聚合器（对应图14中的每一列），专家的基础比率谬误可能有助于提示聚合准确性。

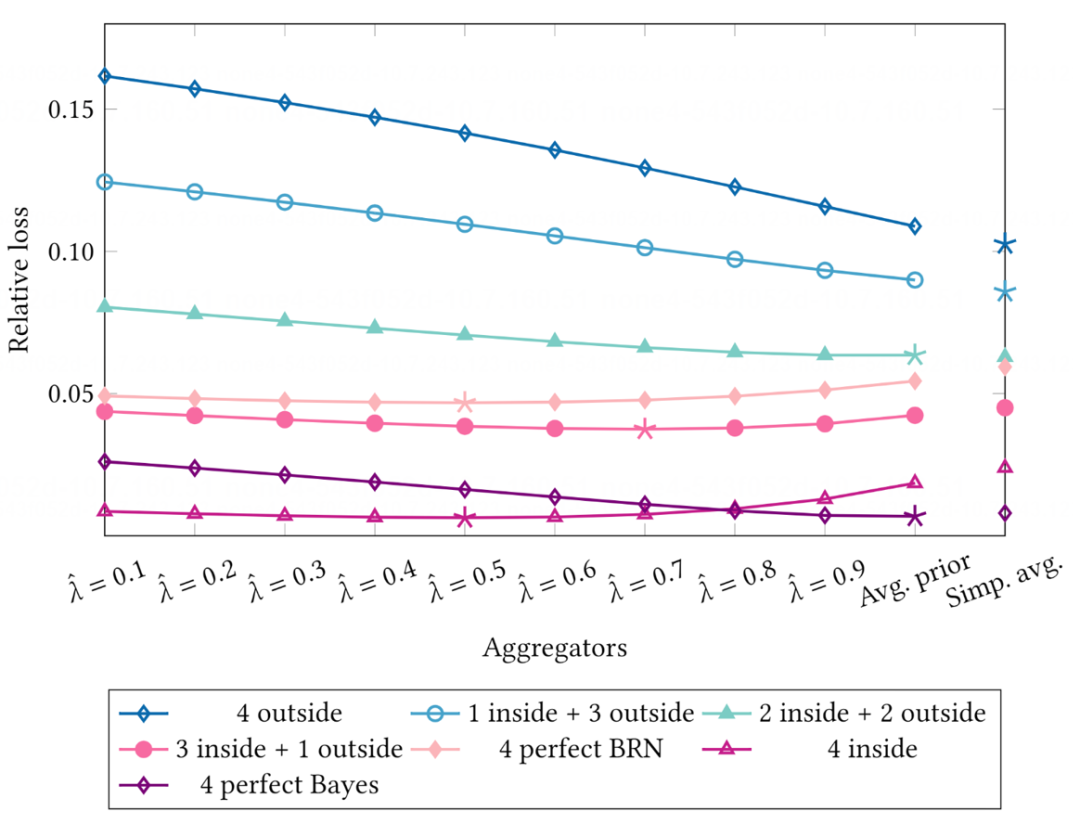
[#3] 如果两个专家回答过 $\mu$ 相同的两个情境 $C_1, C_2$ ，他们在情境 $C_1, C_2$ 上的回答（即两个专家各自在两个任务上的回答，共4个回答）可以形成一组计算聚合器 Regret 所需的输入。我们按照这4个回答的类型划分，将全样本划分成不同子样本。

图14. 聚合器在子样本中的表现

直观解释

我们尝试给上述理论和实验现象一个直观解释：我们的预测聚合问题涉及到三种信息，分别为项目成功的基础比率 $\mu$ ，专家1的私有信号 $s_1$ 和专家2的私有信号 $s_2$ 。当专家是贝叶斯专家时，他们将以1：1的比例混合公共的基础比率信息和他们的私有信号。由于聚合器不知道信息结构，它不能正确地从专家预测中分离出公共信息和私有信息，因此聚合预测往往过度考虑公共的基础比率。

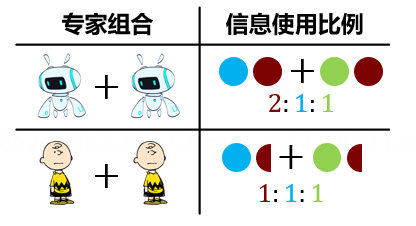
图15. 直观解释

另一方面，当专家的基础比率考虑程度 $\lambda = 0.5$ 时，专家们各自在预测中少考虑了公共信息，反而使聚合结果中三种信息的使用比例得以平衡。

结语

总结来说，一定程度的基础比率谬误可以改进预测聚合。你不必花大价钱咨询完美掌握贝叶斯原则的机器专家们，会犯错误的人类专家反而更能帮助你做好决策。

图16. 基础比率谬误帮助信息聚合

参考文献

[1] Daniel Kahneman and Amos Tversky. 1973. On the psychology of prediction. Psychological Review 80, 4 (1973), 237.

[2] Dan Benjamin, Aaron Bodoh-Creed, and Matthew Rabin. 2019. Base-rate neglect: Foundations and implications. Technical Report.

[3] Itai Arieli, Yakov Babichenko, and Rann Smorodinsky. 2018. Robust forecast aggregation. Proceedings of the National Academy of Sciences 115, 52 (2018), E12135–E12143.

[4] Lawrence D Phillips and Ward Edwards. 1966. Conservatism in a simple probability inference task. Journal of Experimental Psychology 72, 3 (1966), 346.

[5] David M Grether. 1980. Bayes rule as a descriptive model: The representativeness heuristic. The Quarterly Journal of Economics 95, 3 (1980), 537–557.

图文 | 王颖

北京大学孔雨晴课题组

孔雨晴课题组

孔雨晴课题组主要研究计算机和经济、社会科学的交叉方向，包含同伴预测，机制设计，信息设计，认知等级等等，尤其感兴趣和日常生活有紧密联系的研究课题。

课题组相关新闻

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点击“阅读原文”转论文地址

内容中包含的图片若涉及版权问题，请及时与我们联系删除

EC 2024 | 基础比率谬误在预测聚合中的意外价值

评论