大暑 | 浅谈量子复杂性理论

算法复杂性理论的研究基于求解问题需要消耗的资源（如时间资源、空间资源等），通过算法的复杂程度探究问题的难易程度，并建立一个按照计算难度给问题分类的体系。通常我们可以将问题规范化为二元字符串上的判定问题：

定义二元字母表 $\{0,1\}$ 上的语言 $L\subseteq \{0,1\}^*$ 为字母表上一些有穷序列的集合。对于一个语言 $L$ ，相应的判定问题是确定给定字符串输入 $l$ 是否在语言 $L$ 中。例如，我们可以定义全体质数的二进制编码的集合 $\text{PRIME} =\{10,11,101,111,\dots\}$ ，相应的判定问题即判断给定的输入是否是质数。判定问题的另一种表述是将 $L$ 对应于一系列布尔函数（Boolean function） $f_n:\{0,1\}^n \to \{0,1\}$ ， $n$ 对应输入字符串的长度，其中当且仅当输入在语言 $L$ 中时 $f_n$ 的输出是1。

一个复杂性类包含一些难度相近的语言。例如，所有可以在多项式时间里解决的判定问题或者所有可以在多项式空间里解决的判定问题。在经典复杂性理论中，我们有以下几个重要的复杂性类：

P（polynomial）：经典确定性图灵机可以用多项式时间求解的一类问题。
BPP（bounded probabilistic polynomial）：经典非确定性图灵机在多项式时间内可以解决的一类问题（允许在一个输入上的错误概率不超过 $\frac{1}{3}$ ）。
NP（non-deterministic polynomial）：经典确定性图灵机可以用多项式时间验证的一类问题。具体地说，语言 $L\in \text{NP}$ 当且仅当存在一个多项式时间的经典确定性算法 $\mathcal{A}$ ，使得 $x\in L$ 当且仅当存在一个字符串 $y$ （长度至多是 $x$ 的多项式倍），满足 $\mathcal{A}(x,y) = 1$ 。这里 $y$ 称作 $x$ 的一个“见证”。
PSPACE（polynomial space）：经典确定性图灵机可以用多项式空间求解的一类问题。

经典计算复杂性理论证明了这些类的包含关系：

$\text{P}\subseteq NP\subseteq \text{PSPACE},\quad \text{P}\subseteq BPP\subseteq \text{PSPACE}.$ 类似地，我们可以基于量子计算机定义量子复杂性类：

BQP（bounded quantum polynomial）：称语言 $L$ 在 BQP 中，如果存在一个多项式时间的量子算法 $U$ ，满足对 $\forall x\in \{0,1\}^*$ ： $\begin{array}{C} \forall x\in L: \Pr[U \text{ rejects }x]\leq \frac 13; \\ \forall x\notin L: \Pr[U \text{ accepts }x]\leq \frac 13. \end{array}$

上面的错误概率 $\frac 13$ 可以是任意一个 $\epsilon \in (0,\frac 12)$ 。只需要运行算法 $O(\log(1/\epsilon))$ 次并取这些运算结果中占优的答案。
对于量子计算机的“运行时间”，通常我们使用量子电路的计算模型。对于每一个不同的输入长度，我们都需要设计一个相应的接受该输入的量子电路。时间为 $p(n)$ 的量子算法就对应于一族量子电路 $\{C_n\}$ ，其中接受规模为 $n$ 的输入的电路 $C_n$ 应该有不超过 $p(n)$ 个基本量子门。

很显然有 BPP $\subseteq$ BQP，因为对于输入长度 $n$ ，BPP 对应的图灵机可以写成一个由多项式个可逆门组成的电路，它的输入有一部分是随机的比特（对应于算法的随机性）。量子算法可以通过 Hadamard 门生成这些随机的比特，然后运行可逆电路并测量最终的答案。

另一方面，可以证明 BQP $\subseteq$ PSPACE。对于一个多项式时间（ $t=\text{poly}(n)$ ）量子电路 $U_tU_{t-1}\dots U_2U_1|0^n\rangle$ ，我们有 $\langle 0^n | U_tU_{t-1}\dots U_2U_1|0^n\rangle = \sum_{x_1,x_2,\dots x_{t-1}\in\{0,1\}^n} \langle 0^n|U_t|x_{t-1}\rangle \langle 0x_{t-1}|U_{t-1}|x_{t-2}\rangle \cdots \langle x_1|U_1|0^n\rangle.$ 对于确定的 $x_1,x_2\dots x_{t-1}$ ，求和中的对应项可以在多项式时间（自然也是多项式空间）内计算出结果并在多项式空间内存储。经典算法可以枚举所有可能的 $x_1,x_2\dots x_{t-1}$ ，使用多项式大的空间存储当前状态和累加的计算结果，再使用多项式的空间完成每一项的计算过程。

于是我们得到了 BQP 与经典的几个复杂性类的包含关系：P $\subseteq$ BPP $\subseteq$ BQP $\subseteq$ PSPACE。

BQP 与 NP 的关系目前仍是未知的。人们普遍认为 NP 完全问题很可能不在 BQP 中。这种观点的一个直觉是对于无结构化的搜索问题，量子算法相较于经典算法只能实现平方加速（Grover 搜索算法），但对于 NP 完全问题的一个例子——可满足性问题（SAT），目前还没有找到比对 $2^n$ 个赋值暴力搜索显著更快的经典算法。另一方面，BQP 类中很可能也存在一些问题不在 NP 类里。

最后，我们简单考虑从经典的 NP 类出发，在量子计算中定义类似的复杂性类。NP 类定义中的验证算法 $\mathcal A$ 有两个重要的性质：completeness 和 soundness。Completeness 指一个被接受的字符串一定有一个合法的见证，soundness 指被拒绝的字符串没有合法的见证。在量子计算中，我们自然假设验证过程也是量子的。由于量子计算具有固有的概率性，因此在 completeness 和 soundness 条件下我们必须允许有界的误差概率。因此，我们需要首先考虑带概率的见证 MA，然后在其基础上在量子世界定义相应的复杂性类 QMA（而不是 QNP）。

MA（Merlin-Arthur）：称 $L\in \text{MA}$ ，如果存在一个多项式时间的随机算法 $\mathcal A(x,y)$ （ $y$ 就是 $x$ 的见证），对于任意 $x\in\{0,1\}^*$ ，有 $\begin{array}{C} \forall x\in L: \exists y,\Pr[\mathcal A \text{ rejects }x]\leq \frac 13; \\ \forall x\notin L: \forall y,\Pr[\mathcal A \text{ accepts }x]\leq \frac 13. \end{array}$
QMA（Quantum Merlin-Arthur）：称 $L\in \text{QMA}$ ，如果存在一个多项式时间的量子算法 $U(x,|\psi\rangle)$ ，对于任意 $x\in\{0,1\}^*$ ，有

$\begin{array}{C} \forall x\in L: \exists |\psi\rangle,\Pr[U \text{ rejects }x]\leq \frac 13; \\ \forall x\notin L: \forall |\psi\rangle,\Pr[U \text{ accepts }x]\leq \frac 13. \end{array}$

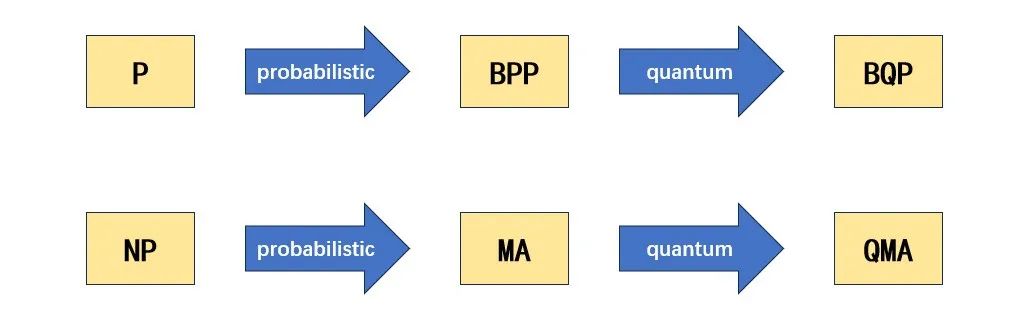
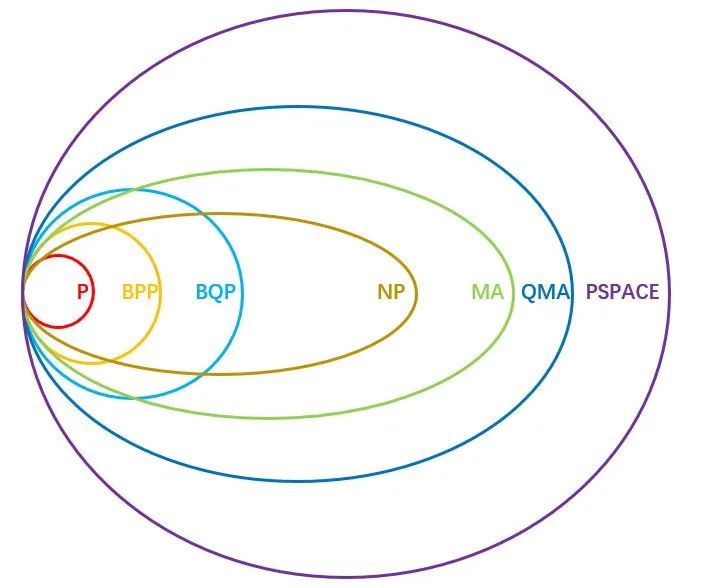
类似于 BQP，很容易证明这些复杂性类之间的包含关系：NP $\subseteq$ MA $\subseteq$ QMA $\subseteq$ PSPACE。

这些复杂性类在多项式时间层次中的具体位置仍然是一个庞大的悬而未决的问题。不过，将一些问题的解作为可以被算法调用的“神谕”（oracle），目前有了一些有趣的结果。对一个语言 $A$ ，我们考虑 $M^A$ 表示一个比通常的计算机更强的机器：它可以在一步计算内确认一个字符串是否属于 $A$ 。我们期望找到一些特殊的谕示，使得我们可以在这些谕示下分离某些复杂性类。

存在一个谕示 $A$ ，使得 $\text{BQP}^A \not \subseteq \text{MA}^A$ ^[1]；
存在一个谕示 $A$ ，使得 $\text{NP}^A\not \subseteq \text{BQP}^A$ ^[2]。

量子算法为经典复杂性理论打开了一扇新的大门。从经典的各种证明系统和复杂性类出发，我们可以在量子世界建立对应的量子复杂性类，乃至构造出经典-量子混合的证明系统。一方面，对于量子复杂性理论的研究有助于进一步完善经典复杂性理论，例如，证明 BQP 严格真包含 BPP（比如证明经典随机化计算机不能有效地解决因式分解问题）将推导出P $\neq$ PSPACE。另一方面，随着量子计算的发展，许多现有的加密算法和安全协议可能不再可靠。量子复杂性理论的研究不仅告诉我们那些问题在量子计算机上容易解决，还指引我们开发抗量子攻击的新型加密算法和协议，确保后量子时代下的数据安全。

参考文献

[1] László Babai. Bounded round interactive proofs in finite groups. SIAM Journal on Discrete Math,5(1):88–111, 1992.

[2] Charles H. Bennett, Ethan Bernstein, Gilles Brassard, Umesh Vazirani. Strengths and weaknesses of quantumcomputing. SIAM Journal on Computing, 26(5):1510–1523, 1997.

[3] Ronald De Wolf. Quantum computing: Lecture notes[J]. arXiv preprint arXiv:1907.09415, 2019.

[4] John Watrous. Quantum computational complexity[J]. arXiv preprint arXiv:0804.3401, 2008.

[5] 李彤阳. 北京大学《量子计算》课程. https://quantumcomputation.tech/.

文 | 张业鑫

图 | 李凯

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

内容中包含的图片若涉及版权问题，请及时与我们联系删除

大暑 | 浅谈量子复杂性理论

评论