Nat. Commun. | 一种稳健的顺式孟德尔随机化方法及其在药物靶点发现中的应用

今天为大家介绍的是来自Wei Pan团队的一篇论文。孟德尔随机化（MR）使用遗传变异作为工具变量（IV）来研究性状之间的因果关系。与传统的MR不同，顺式MR仅使用顺式SNP去关注单个基因组区域。例如，使用一种蛋白质的顺式pQTL作为疾病的暴露因子，为药物靶点发现开辟了一条成本有效的路径。然而，极少有方法能够有效处理顺式SNP的多效性和连锁不平衡（LD）。在此，作者提出了基于约束最大似然法的cisMR-cML方法，该方法对工具变量假设的违背具有很强的理论支持。作者进一步阐明了当前建模边际遗传效应而非条件遗传效应，以及仅在顺式MR分析中使用暴露相关SNP的做法所带来的严重但被广泛忽视的后果。数值研究表明，作者的方法优于现有的其他方法。在对冠状动脉疾病（CAD）进行的药物靶点分析中，包括一个蛋白质组范围的应用，作者确定了三个潜在的CAD药物靶点，分别是PCSK9、COLEC11和FGFR1。

孟德尔随机化（MR）是一种广泛使用的方法，通过遗传变异作为工具变量（IV）来推断两个性状之间的因果关系，一个性状称为暴露，另一个称为结果。由于遗传变异在受孕时是随机分配并固定的，这减少了混杂因素和反向因果关系的风险。在IV回归框架内，MR要求三个有效的IV假设以获得有效推论：IV必须（1）与暴露相关；（2）与暴露-结果关系的任何混杂因素无关；（3）在控制暴露和混杂因素后，与结果无关。基于这些假设，MR可以提供暴露与结果之间（假定的）因果关系的证据，并可应用逆方差加权（IVW）方法。然而，只有第一个IV假设可以被检验，并且在实践中通过使用与暴露相关的全基因组显著SNP相对容易满足；相对而言，第二和第三个假设无法实证检验，并且由于广泛存在的（水平）多效性，可能被违反。在存在水平多效性的情况下，已经提出了许多MR方法，但大多数方法要求使用独立的IV，这在大多数MR分析中是常见的。

与此同时，MR研究越来越关注使用一些局部和相关的顺式SNP作为IV的小基因组区域，即顺式MR。顺式MR最有前途的应用之一是药物靶点发现，包括药物靶点的优先排序、验证或重新定位。药物靶点MR分析使用一种蛋白质（作为潜在的药物靶点）或其下游生物标志物作为暴露，使用编码该蛋白质的基因的顺式SNP作为IV。尽管这种分析具有重要意义，但它仍然关键依赖于三个有效的IV假设。使用蛋白质作为暴露使违反无水平多效性假设的可能性降低，因为蛋白质在许多传统/多基因MR使用的常见风险因素上游，然而，即使在同一个基因/蛋白质区域的顺式SNP中，不同的生物机制仍可能存在。事实上，仅有一个或两个SNP时，许多稳健MR方法无法应用。最后，更重要的是，正如后续数值研究所示，仅使用独立SNP很可能导致分析中缺乏有效的IV，因为它们与区域内其他SNP相关。作为替代，作者更愿意在顺式MR中使用多个相关的IV。然而，只有少数顺式MR方法对IV假设的违反具有稳健性。

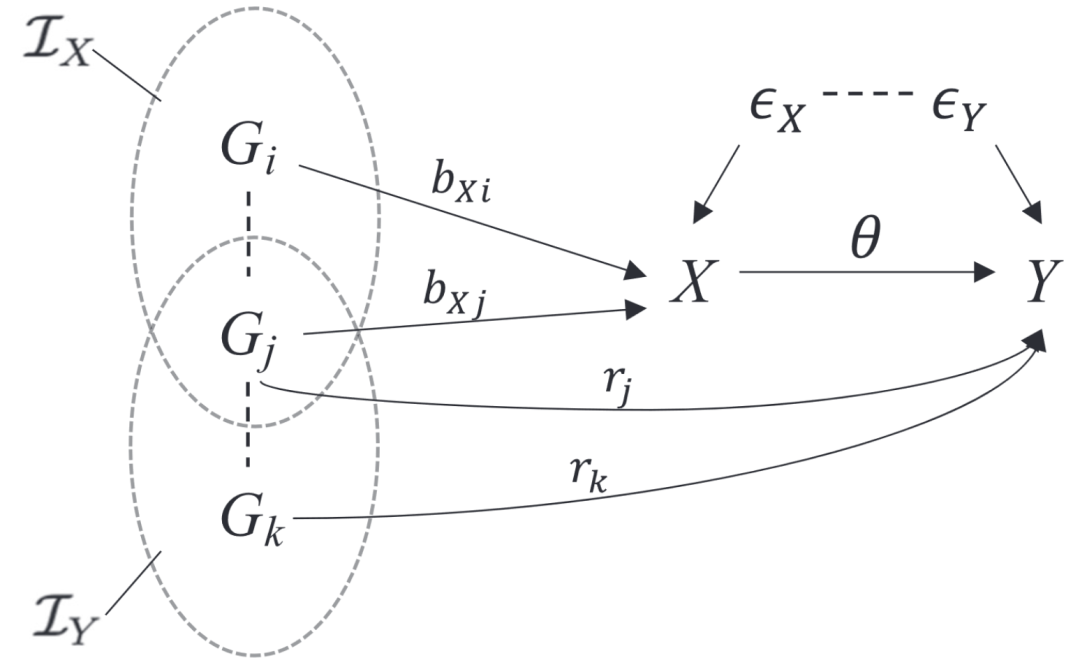
图 1

作者提出了cisMR-cML方法，用于估计暴露（如基因或蛋白质）对结果的因果效应，即使在存在无效IV的情况下，也能使用公开的GWAS总结数据。这是对MR-cML的重要扩展，允许将相关SNP作为分子暴露（如基因或蛋白质）的IV。通过允许使用相关IV，cisMR-cML适用于顺式MR分析，而在顺式区域内使用MR-cML可能无法获得至少三个独立的IV。此外，cisMR-cML相比MR-cML有两个关键区别，增强了其对无效IV的稳健性。首先，如一般因果模型图1所示，cisMR-cML建模了SNP与暴露之间的条件效应，以及SNP与结果之间的条件效应，这不同于MR-cML和其他MR方法中建模边际GWAS估计的传统方法。这一区别显著减轻了在顺式MR中处理相关SNP时引入额外（且不必要）水平多效性的风险。其次，不同于通常只使用与暴露相关的SNP，cisMR-cML使用与暴露或结果共同相关的变异作为IV，即中的变异。作者使用一种称为GCTA-COJO的条件和联合关联分析来选择这些变异。正确考虑与结果相关的SNP进一步有助于避免额外的水平多效性。尽管cisMR-cML中提出的这两个基本考虑在统计上看似简单，但在当前的顺式MR应用中却常被忽视。例如，两种最广泛使用的顺式MR方法——广义IVW和广义Egger，直接建模边际GWAS估计；最近的两个药物靶点应用（如Zhao等人和Zheng等人）在选择条件独立的pQTL后也应用了这些方法。

一旦选择了作为候选工具变量（IV）的遗传变异，就可以使用公开的参考面板估计这些变异之间的连锁不平衡（LD）矩阵。然后将GWAS总结数据中的边际估计转换为条件GWAS估计。接着，在双样本MR框架下，在无效IV数量有限制的情况下，使用最大似然框架实现cisMR-cML，该限制考虑了水平（相关和/或无关）多效性。无效IV的数量通过贝叶斯信息准则（BIC）一致性选择。简而言之，cisMR-cML从候选集中选择有效的IV，以推断X到Y的因果关系。作者建立了统计理论，以证明cisMR-cML的一些理想属性，例如在存在相关或无关多效性的无效IV时的估计一致性和渐近正态性。最后，作者还实施了一种数据扰动（DP）方法，以考虑模型选择的不确定性。给定K值下，作者提出的的cisMR-cML算法如图2所示。

图 2

作者进行了两组模拟研究，比较了作者提出的方法（除非另有说明，均使用数据扰动）与其他现有的顺式MR方法，包括广义IVW和Egger（GIVW和GEgger）、考虑LD的Egger（LEgger），以及这些方法的不同实现。在第一组模拟研究中，作者从自回归LD模式中直接生成了10个SNP的GWAS总结统计数据，分别对应弱相关（ρ = 0.2）、中等相关（ρ = 0.6）和强相关（ρ = 0.8），并考虑了两种情景：（1）所有10个SNP都对暴露有影响，即；（2）只有一半的SNP对暴露有影响，即，且 = 2。在这两种情景中，作者改变了中无效IV的数量，记为。作者使用了几种方法：cisMR-cML和LEgger，基于所有10个SNP计算条件估计；GIVW和GEgger，基于边际GWAS估计。在情景（1）中，作者还选择了独立的IV（）并应用了IVW、Egger和MR-cML的独立版本，基于边际GWAS估计。作者将这些实现称为IVW-IND、Egger-IND和cML-IND。作者进一步应用了四种可以考虑LD的多基因MR方法，但这些方法并未专门为顺式MR分析提出，包括MR.LDP、MR.Corr2、MR.CUE和MRAID。在情景（2）中，作者还研究了仅使用中的SNP的不同顺式MR方法的表现。具体来说，作者应用了cisMR-cML和LEgger，基于中的5个SNP计算条件估计；应用了GIVW和GEgger，使用中5个SNP的GWAS总结数据。作者将这些实现分别称为cisMR-cML-X、LEgger-X、GIVW-X和GEgger-X。

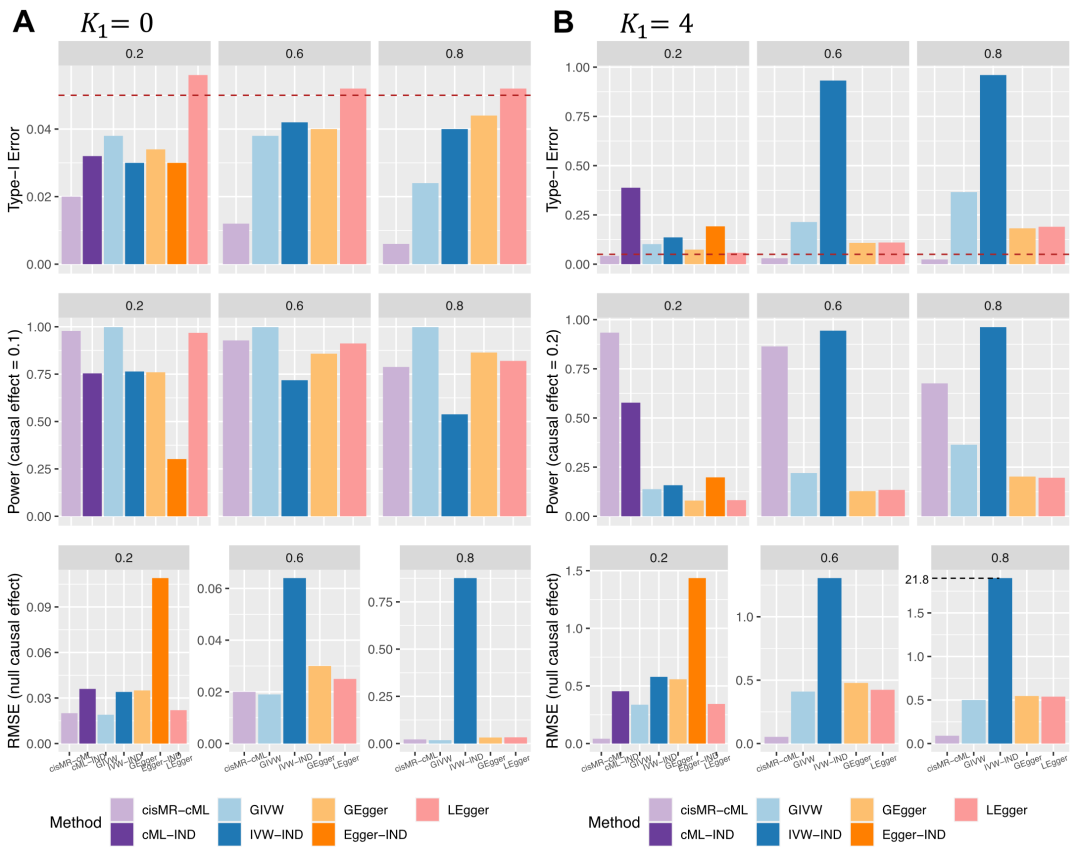
图 3

在第一个情景中，所有10个IV都对暴露有影响（），代表性结果展示在图3中。在整个模拟过程中，作者在显著性水平5%评估了I型错误率。首先，当所有10个IV都有效时（图3A），所有方法的I型错误率都控制得很好。在这种理想情景下，没有无效IV的情况下，cisMR-cML（采用数据扰动实现）比其他方法更保守，这与之前在MR-cML和MVMR-cML中的观察结果相似。需要注意的是，即使在这样的理想情景中，GEgger的均方根误差（RMSE）相对较大（估计值不够精确），这可能是由于方法中实施的等位基因方向步骤。IVW-IND、Egger-IND和cML-IND的效能都低于它们的相关版本对应方法，即GIVW、GEgger和cisMR-cML。

在存在4个无效IV的情况下（图3B），只有cisMR-cML能够控制I型错误率，同时保持高效能。此外，它的RMSE远低于其他三种方法。另一方面，随着SNP之间相关性的增加，GIVW、GEgger和LEgger的I型错误率也逐渐增加。使用独立IV的三种方法的I型错误率也显著增高，因为无效IV的直接效应被吸收到分析中使用的边际GWAS效应中。四种多基因MR方法表现不稳定，表现为极低的效能、增高的I型错误率或未成功收敛。最后，作者进一步研究了在cisMR-cML中使用边际GWAS估计，cisMR-cML-Marg由于边际模型中多重性假设的违反，导致I型错误率显著增加。

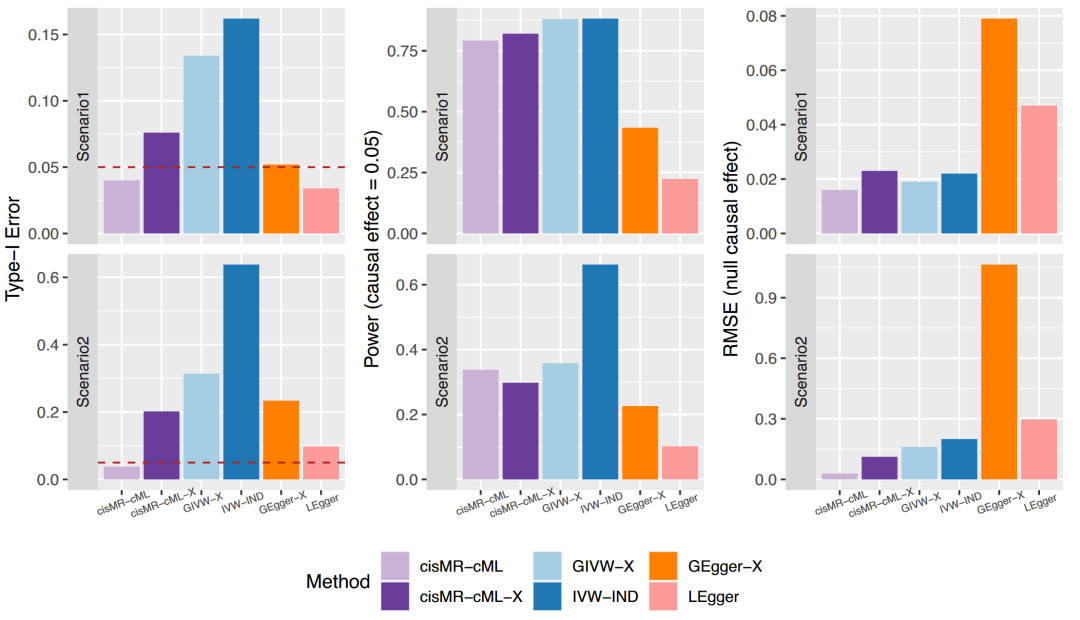
图 4

在第二种情景下，只有5个SNP对暴露有影响，作者进一步研究了仅使用这5个SNP数据的四种方法的表现，如图4中的“-X”后缀所示。当K1 = 0时（图4A），似乎中的所有IV都是有效的。然而，由于它们与中的SNP相关，如果没有包括中的SNP，它们吸收了中SNP对结果的直接效应。因此，中的所有IV都变得无效，并且在cisMR-cML-X中违反了多重性条件，导致I型错误率显著增加。同样，仅使用与暴露条件相关的SNP的GIVW-X和GEgger-X也导致了I型错误率增加。另一方面，使用所有10个SNP的cisMR-cML在所有情景中都能很好地控制I型错误率，保持高效能并具有最小的RMSE。通过这个例子，可以看出在计算条件估计时，包括中的SNP的重要性，因为否则，cisMR-cML所需的多重性条件可能会被违反（除非和中的SNP之间没有或很少有LD）。此外，值得一提的是，当K1 = 1时（图4B），在cisMR-cML使用的10个IV中，有些仅违反了“相关性”假设，有些仅违反了“无水平多效性”假设，但也有些同时违反了这两个假设。值得注意的是，该方法在存在不同类型的无效IV情况下表现稳健，产生了无偏估计并很好地控制了I型错误率。

编译 | 黄海涛

审稿 | 曾全晨

Lin, Z., & Pan, W. (2024). A robust cis-Mendelian randomization method with application to drug target discovery. Nature Communications, 15(1), 6072.