
新智元报道
新智元报道
【新智元导读】组合数学领域的一个难题,完全无序的数学不可能性,被UCLA华人研究生和两位MIT研究生取得了突破!为此,他们强化了陶哲轩的一项成果,并再进一步。这是数十年来该领域的首次进展。
刚刚,组合数学领域最大的未解之谜之一——完全无序的数学不可能性,取得了数十年来的首次进展。
突破这项成就的是,是UCLA的华人研究生James Leng,以及两位MIT研究生Ashwin Sah和Mehtaab Sawhney。
今年2月,三人宣布,他们对整数集合在必须包含间隔均匀的数字序列(如{9, 19, 29, 39, 49}或{30, 60, 90, 120})之前能有多大的估计值,进行了长期的改进。
这个证明,即是组合数学领域最大的未解决问题之一。

论文地址:https://arxiv.org/abs/2402.17995
这一成果,也在数学圈内引起了轰动。
牛津大学数学家Ben Green表示,几位学生的成果,令人印象深刻。尤其是成果发布时,三人都还在读研究生。
算术级数问题
级数(progression)是一列展现出特定模式的数或项,即每一项都对前一项应用特定规则而得到,也可称之为序列。
数学中,级数主要有三种类型,包括算数级数、几何级数以及调和级数。
有规则间隔的数字序列,称为算术级数(arithmetic progression),我们更熟悉的说法是等差数列。

尽管模式简单,但它们背后隐藏着令人震惊的数学复杂性。
更神奇的是,无论我们怎样努力,算术级数都很难避免。
1936年,数学家Paul Erdős和Pál Turán推测,如果一个集合由整数的非零分数组成(哪怕只有0.00000001%),那么它一定包含任意长的算术级数。

唯一可以避免算术级数的集合,就是那些包含整数「可忽略不计」部分的集合。
例如,集合 {2, 4, 8, 16, …},其中每个数字都是前一个数字的两倍,它沿着数轴分布得如此分散,以至于可以说它占据整个数字集合的0%。
因此,这个集合没有级数。
四十年后的1975年,这个猜想被一位叫Endre Szemerédi的数学家证明了。
而他的工作,催生了众多研究方向,至今仍在令数学家们探索。
Sah和Sawhney的MIT博导Yufei Zhao这样介绍道:「他证明中的许多想法,都发展成了自己的世界」。


算术级数达到4项时,就会「咬人」


华人研究生,打破研究阻碍
2022年,当时正在UCLA读研究生二年级的Leng,开始研究Gowers的理论。 他脑子里并没有装着Szemerédi定理,相反,他希望自己能解决一个由Gowers发展出的技巧相关的问题。 其他数学家并不看好,担心他解决问题所需要耗费的精力太大了,与之相比可能得到的结果根本不值一提,于是纷纷劝阻他。 Leng后来评价道:「他们是有道理的。」 整整一年多的时间,他都一无所获。 但是某一天开始,他忽然做出了某些东西。 而一直在研究相关问题的Sah和Sawhney看到他的工作后,表示了巨大的兴趣。 用Sawhney的话说,「我很惊讶,居然还可以这样思考。」 
他们意识到,Leng的研究可能帮助他们在Szemerédi定理上取得进展。 几个月后,他们做到了! 这三位年轻的数学家想到了一个办法,在没有五项技术的情况下,获得了更好的集合大小上限。(也就是我们开头看到的那篇论文) 然后,他们将工作扩展到了任意长度的级数,这标志着Gowers证明以来的23年里,这个问题首次取得了进展。 Gowers已经证明,当起始数字池变大时,我们可以做出的避免进展的集合,会以某种速度变得相对较小。 而现在, Leng、Sah和Sawhney证明,这种情况发生的速度要快得多。 而导师Zhao对学生们的工作赞不绝口:「这是一项巨大的成就。但我不会建议任何学生攻克这种问题,因为它真的太难了。」 许多数学家都对三人获得新界限方法感到非常兴奋。 为了顺利解决问题,他们必须先强化一项先前的、技术性更强的成果。 这项成果来自牛津大学的Ben Green、陶哲轩和希伯来大学的Tamar Ziegler。 
数学家们认为,这一结果(Gowers理论的某种阐述)可以进一步改进。 Green介绍说:「我的感觉是,我们对这个理论的理解也并不完善,我们只是看到了它的一些影子。」 自从2月份发表这篇论文后,Sawhney已经完成了他的博士学位。现在,他是哥大的一名助理教授。 Sah仍然在MIT攻读研究生。



论文概述
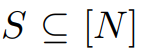 中最大的S。
中最大的S。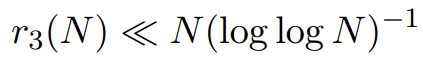 。
。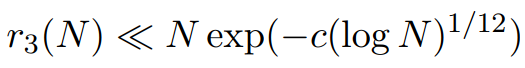 。
。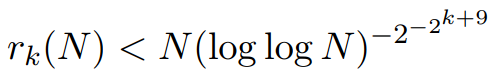 。
。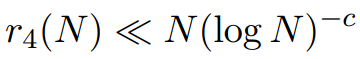 。
。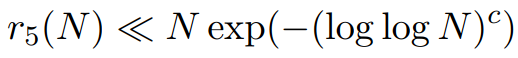 。
。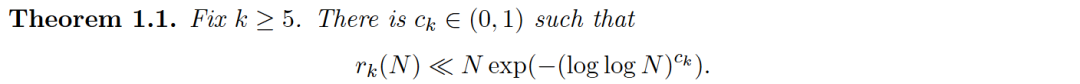

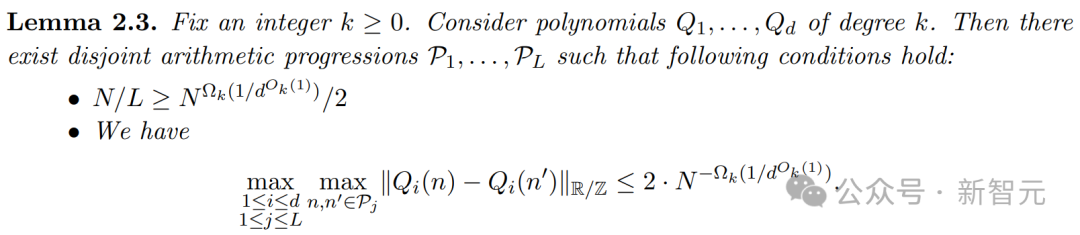
MIT本科生,推动图论研究前沿



作者介绍
James Leng本科毕业于加州大学伯克利分校,目前是UCLA数学系的在读研究生,与陶哲轩共同合作。他的研究领域包括算术组合数学、动力系统和傅里叶分析,主要关注高阶傅里叶分析。 
Ashwin Sah从2020年起成为MIT的数学系研究生,由Yufei Zhao指导,研究兴趣包括组合数学、概率论和数论。 
Mehtaab Sawhney目前是哥伦比亚大学助理教授,同时担任Clay数学研究所的研究员,他的研究同样关注组合数学、概率论和理论计算机科学。 
在俄勒冈州波特兰长大的Sah,16岁时获得奥数金牌,17岁就读于MIT,两年半后毕业。 在MIT的第一年,他上了Yufei Zhao教授的两门课,其中一门是关于组合学的研究生水平讨论课。 在全世界最有才华的数学学生中,Sah仍然能脱颖而出。







内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢