处暑 | 从热力学与统计物理到信息论编码——浅谈“熵”

熵最先来源于物理学家克劳修斯，他受到卡诺对热机效率描述时热温比 $\frac QT$ 形式的启发，把热温比这个量叫做 entropy，词根同时含有“能量”和“转变”两层意思。后来克劳修斯和玻尔兹曼等科学家将熵在热力学中的内容完善，并在统计物理中让熵大放异彩，熵被引入概率论后香农又将其推广，创建了信息论。可以说，随着熵这一概念的发展和扩充，多门学科得以创立和完善，熵这一看不见摸不着，甚至很难直观量化或感知到的概念颇具传奇色彩。

在本文中，笔者统合了熵在热学，统计物理和信息论中的基础概念和推导，梳理了它们的统一性和脉络。

宏观状态下的克劳修斯熵

1.1 克劳修斯定理

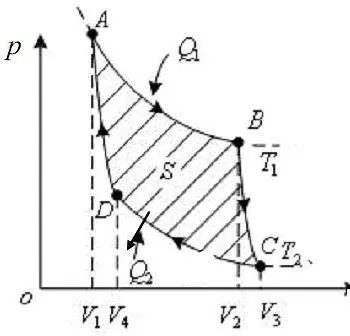
如上图，我们取工作于任意两个状态 $A,C$ （温度分别为 $T_1,T_2$ ）可逆卡诺热机（其实任意两个状态之间都可以看作无数微卡诺循环进行）。我们规定数学上 $đQ>0$ 代表系统吸收热量，反之亦然，那么有： $\int_A^C\frac{đQ}T=常量=S_C-S_A$ 由卡诺定理，任何热机的效率，总是小于等于在两个相同温度之间工作的理想卡诺热机，即 $\eta_{热机}\leq\eta_{可逆}$ 带入热机的效率计算公式，因此有 $\begin{align}\frac{Q_1+Q_2}{Q_1}\leq\frac{Q_{1可逆}+Q_{2可逆}}{Q_{1可逆}}\tag{1}\end{align}$ 可逆热机的必要充分条件是： $\eta=\frac{Q_{1可逆}+Q_{2可逆}}{Q_{1可逆}}=\frac{T_1-T_2}{T_1}$ 或者写为： $\begin{align}\frac{Q_{2可逆}}{Q_{1可逆}}=-\frac{T_2}{T_1},\tag{2} \end{align}$ （负号是因为吸放热符号不同）。

将 (2) 式带入 (1) 式，可得 $\begin{align}\frac{Q_1}{T_1}+\frac{Q_2}{T_2}\leq0\tag{3}\end{align}$ 将大量 (3) 式的微卡诺循环迭加在一起时，有 $\begin{align}\oint\frac{đQ}T\leq0\tag{4}\end{align}$ (4) 式就是广为人知的克劳修斯定理。

1.2 孤立系统的熵为何只增不减

克劳修斯定理就是热力学第二定律的数学解释，它是怎么得到熵增的结论的呢？结合 (1), (4) 式，可以推出 $\substack{\int_A^B\frac{đQ}T\\{可逆或不可逆}}\leq\substack{\int_A^B\frac{đQ}T\\{可逆}}$ 按照熵的定义，有 $\substack{\int_A^B\frac{đQ}T\\{可逆}}=S_B-S_A$ 因此可得 $\substack{\int_A^B\frac{đQ}T\\{可逆或不可逆}}\leq S_B-S_A$ 写为微分形式，即 $\begin{align}\frac{đQ}T\leq \mathrm{d}S\tag{5}\end{align}$ 其中，等号只适用于可逆变化的情况那么，对于孤立系统，与外界没有热接触，取 $đQ=0$ ，我们得到 $\mathrm{d}S\geq0$ 就是俗称的熵增原理，笔者随后会从统计物理学中重新分析。

1.3 总结：合并了热力学第一、第二定律的微分式

热力学的两个定律的流行表述是：

1. 第一定律：宇宙的能量是常量

2. 第二定律：宇宙的熵趋向最大值

写成基本算式，就是：

$\begin{array}\\đQ=\mathrm{d}U+p\mathrm{d}V \\ \mathrm{d}S=\frac {đQ}T\end{array}$ 联立得 $T\mathrm{d}S=\mathrm{d}U+p\mathrm{d}V$ 为了适应更普遍的情况，我们用广义力的集合 $X_i$ ，把系统做的功写作 $T\mathrm{d}S=\mathrm{d}U+\sum X_i\mathrm{d}x_i$ 由此我们可以得到在统计物理中更有意义的式子 ${(\frac{\partial S}{\partial U})}_V=\frac1T$ 即在恒定体积下，熵 $S$ 对内能 $U$ 的偏导确定了热力学温度 $T$ 。

微观视角下的熵与熵的统计意义

2.1 玻尔兹曼熵与概率

2.1.1 概率视角

玻尔兹曼用系统状态随机出现的概率描述系统的无序度，并确立了这个概率和系统的熵的关系。假定有两个独立且不同的平衡态系统， $p_1,p_2$ 分别是这两个系统独自出现的概率，这两个状态同时出现的概率是 $p=p_1*p_2$ ，我们用 $S_1,S_2$ 代表系统1和系统2的熵，因为熵是广延量，故总熵为 $S=S_1+S_2$ 这和信息熵的推导非常像，因为信息论的熵就是源于这里。

因此如果熵和概率有关，那么两者之间的关系就必须是一个对数关系，即 $\begin{align}S=C\ln p\tag{6}\end{align}$ 其中 $C$ 是一个常数。

2.1.2 玻尔兹曼熵

微观态数目 $\Omega$ 是最重要的物理量之一，我们希望通过微观态数目 $\Omega$ 从微观上引入熵的概念。简单来说，顾名思义，微观态数目就是一个体系微观下可能的状态的数目，类似于“从黑盒中有可能摸出五个种类的笔”这样的描述，那么对两个系统 $A$ 和 $B$ ，以及他们形成的大系统 $A+B$ ，他们之间的微观态数目的关系是什么呢？这就类似于“黑盒中有 $\Omega_A$ 种笔，有 $\Omega_B$ 种本，随手摸一个笔一个本，有几种可能的情况”，所以有 $\Omega_{A+B}=\Omega_A*\Omega_B$ 剩下的推导和上面 2.1.1 推导一样，不难得到 $\begin{align}S=k\ln\Omega\tag{7}\end{align}$ 其中 $k$ 是常数，并且计算验证是玻尔兹曼常数（随后会具体证明），这里定义的熵叫玻尔兹曼熵，也叫微观熵。

2.2 克劳修斯熵（宏观熵）与玻尔兹曼熵（微观熵）的统一

在 2.1 中我们了解了宏观状态下的克劳修斯熵，也在刚才推出了玻尔兹曼熵的形式，那么他们有什么具体联系呢？为区别两种熵，我们管克劳修斯熵叫 $S_C$ ，管玻尔兹曼熵叫 $S_B$ 。

2.2.1 玻尔兹曼系统

假设对一个系统，其中的粒子可以分辨，它一共有 $N$ 个粒子，有 $i$ 个能级，每个能级上都可以放置无数个粒子，第 $i$ 能级上的粒子数为 $N_i$ ，能量态为 $\epsilon_i$ ，简并度为 $g_i$ （简并度的通俗化解释：比如对于绕原子核公转的电子，每个能级的电子最多有两种自旋，则简并度为2）那么毫无疑问，玻尔兹曼系统的微观态数目为： $\Omega=\frac{N!}{\prod_iN_i!}\prod_ig_i^{N_i}$

2.2.2 微观熵与宏观熵关系的推导与表述

对于简单情况下的玻尔兹曼系统，我们令 $g_i=1$ ，则有 $\Omega=\frac{N!}{\prod_iN_i!}$ ，则 $\ln\Omega=\ln N!-\ln\prod_iN_i!=\ln N!-\sum_i\ln N_i!$ 由粒子数守恒得知， $\mathrm{d}N=0$ ， $\mathrm{d}\ln N!\cong \mathrm{d}[N\ln N-N]=\ln N\mathrm{d}N+N\frac{\mathrm{d}N}N-\mathrm{d}N=0$ ，于是 $\mathrm{d}\ln\Omega=-\sum_i\mathrm{d}(N_i\ln N_i-N_i)=-\sum_i(\ln N_i)\mathrm{d}N_i$ 对于能量组态 $\{\epsilon_i\}$ ，由波尔兹曼分布 $N_i=g_ie^{-\alpha-\beta\epsilon_i}$ 玻尔兹曼分布应该大伙都有所耳闻就不多介绍了，其中 $e^{-\alpha}=N_0$ ， $\beta=\frac1{k_BT}$ ， $\epsilon_i$ 可以粗浅地理解为能量 $E$ ，不管 $g_i$ 的话，玻尔兹曼分布可以写成我们常见的形式： $N_i=e^{-\alpha-\beta\epsilon_i}=N_0e^{-\frac E{k_BT}}$ 如果对玻尔兹曼机有了解的话，应该知道它和能量有关，那个系数就是玻尔兹曼分布后面的系数 $e^{-\frac E{k_BT}}$ 。

回到我们对玻尔兹曼分布的严谨定义，在 $g_i=1$ 时，有 $\ln N_i=-\alpha-\beta\epsilon_i=\ln N_0-\beta\epsilon_i$ 带回上式，所以有 $\mathrm{d}\ln\Omega=-\sum_i(\ln N_0-\beta\epsilon_i)\mathrm{d}N_i=-\ln N_0\sum_i\mathrm{d}N_i+\beta\sum_i\epsilon_i\mathrm{d}N_i=\beta\sum_i\epsilon_i\mathrm{d}N_i$ 由能量守恒，外界做功等于内部状态能量增加 $đW=\sum_iN_i\mathrm{d}\epsilon_i$ 由热力学第一定律可知 $\mathrm{d}E=\mathrm{d}\sum_iN_i\epsilon_i=\sum_iN_i\mathrm{d}\epsilon_i+\sum_i\epsilon_i\mathrm{d}N_i=đQ+đW$ 比较上述两式，我们有 $\sum_i\epsilon_i\mathrm{d}N_i=đQ$ 将该结果带入 $\ln\Omega$ 的代表式，则 $\mathrm{d}\ln\Omega=\betađQ$ 将 $\beta=\frac1{k_BT}$ 代入，则得 $\begin{align}k_B\mathrm{d}\ln\Omega=\frac{đQ}T\tag{8}\end{align}$ 这里已经看到了我们想要的形式，等式左边是玻尔兹曼熵 $S_B$ 的形式，右边是克劳修斯熵 $S_C$ 的形式。

显然 $k_B$ 和我们在 2.1.2 推出的 (7) 式的 $k$ 在量纲和形式上都符合，因此 $k_B\mathrm{d}\ln\Omega=\mathrm{d}S_B$ ，于是有 $\mathrm{d}S_B=\frac{đQ}T$ 宏观上， ${\frac{đQ}T|}_{可逆}=\mathrm{d}S_C$ ，所以 $\mathrm{d}S_B=\mathrm{d}S_C$ 因此，只要选取同样的参考点，热力学系统的玻尔兹曼熵与克劳修斯熵完全相同 $S_B=S_C$

2.3 熵的统计意义——概率和状态数目的统一

系统如何趋向平衡？统计语言中，热的流动是让系统的态密度增加。我们在此只进行定性和半定量的不算特别严谨的分析。由之前的结论，我们有 $S=S_B=k_B\ln\Omega$ 因为微观状态数目 $\Omega$ 小意味着无序程度降低，所以熵是宏观的热力学系统对应的无序程度的度量，也就是宏观态出现概率大小的标志。熵高意味着系统包含的微观态数目多，从而宏观态出现的概率大，也就是混乱、分散，无序程度高再把目光放到 (4) 式——克劳修斯定理： $\begin{align}\oint\frac{đQ}T\leq0\tag{4}\end{align}$ 对于不可逆过程，式子不能取等。也就是说非理想热机（或者就是自然界的能自发发生的过程）会不可避免地将一些能量从高温热库直接泄露到低温热库而没有对外做功。而根据热力学第二定律，能量又不能自发从低温热库跑到高温热库而不引起其他影响，因此泄露的能量就“贬值”了，这些能量被称为无用能。由此知，熵增意味着又用能减少，被贬值的无用能增多。

吉布斯熵与信息

3.1 香农定理

1948年，香农发现了香农定理，此后才能在信息论的基础熵，十分普遍地讲述统计方法。概率论中，香农定理是一个最基础的定理，它能描述为：如果一个系统的n个事件具有彼此独立的概率 $p_i\,\,\,(i=1,2,\cdots,n)$ ，那么存在一个独特的函数 $\begin{align}f(p_1,p_2,\cdots,p_n)=-C\sum_i^np_i\ln p_i\tag{9}\end{align}$ 对于一组给定的约束，当函数 $f$ 取最大值时， $p_i\,\,\,(i=1,2,\cdots,n)$ 是系统的最概然分布。

3.2 吉布斯熵

按照香农定理，在没有任何约束条件时，最有可能的概率分布是所有事件的概率都一样 $-\sum_i^np_i\ln p_i$ 取最大值的情况是所有的 $p_i$ 彼此相等的情况，这与熵增定理惊人的相似，直接导致了吉布斯熵的定义： $S=-k\sum_ip_i\ln p_i$ 因此这个函数的最大值与系统的最概然分布对应，这里的熵可以用于平衡态或非平衡态对应信息论中，信息的定义为： $信息=k\sum_ip_i\ln p_i$ 是个负值，所以信息也叫做负熵。

参考文献

[1] Waldram J R. The Theory of Thermodynamics[M], Cambridge: Cambridge University Press, 1985.

[2] Malcolm Longair. Theoretical Concepts in Physics[M], 安徽合肥：中国科学技术大学出版社, 2017.

[3] Kittel C. Thermal Physics[M], New York: John Wiley and Sons, 1969.

[4] 刘玉鑫. 热学[M], 北京：北京大学出版社, 2016.

[5] 赵凯华, 罗蔚茵. 热学[M], 北京：高等教育出版社, 2005.

[6] 舒幼生. 物理学难题集萃[M], 北京：北京大学出版社, 2016.

[7] 郑永令. 国际物理奥赛的培训与选拔[M], 上海：复旦大学出版社, 2017.

[8] 刘斌. 信息论与编码课程（中科大）[信息论基础课程主页 (ustc.edu.cn)](http://home.ustc.edu.cn/~kunzhao/).

文 | 张越凯

图 | 朱成轩

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

内容中包含的图片若涉及版权问题，请及时与我们联系删除

处暑 | 从热力学与统计物理到信息论编码——浅谈“熵”

评论