液态神经网络 (Liquid Neural Nets,LNNs) 是 AI/ML 研究领域中一个令人兴奋的、相对较新的方向,有望实现更紧凑、更动态的时间序列预测神经网络。LNNs 为以下任务提供了一种新方法,如天气预报、语音识别和自动驾驶。LNNs 的主要优势在于,它们在训练后能够继续适应新的激励https://techcrunch.com/2023/08/17/what-is-a-liquid-neural-network-really/。此外,LNNs 在噪声条件下具有鲁棒性,并且比传统网络更小,更具可解释性。

LNN 和类似概念已经存在了一段时间,但 2020 年的论文《液态时间常数网络Liquid Time Constant Networks》https://arxiv.org/abs/2006.04439 将它们推到了 AI/ML 领域的最前沿。从那时起,它们就成为时间序列预测器的一个迷人方向,旨在提高单个神经元的表征能力,而不是通过规模获得能力。
在开发 LNN 概念时,Hasani直接受到了线虫 C. Elegans(一种微小的蛔虫)中的生物神经元的启发https://abdulkaderhelwan.medium.com/liquid-neural-networks-37ccaaee469a。2020 年论文的主要作者Ramin Hasani指出https://news.mit.edu/2021/machine-learning-adapts-0128, “它的 C. Elegans 神经系统中只有 302 个神经元,但它可以产生出乎意料的复杂动态。”Elegans的使命是“拥有更少但更丰富的节点”。结果就是 LNN。
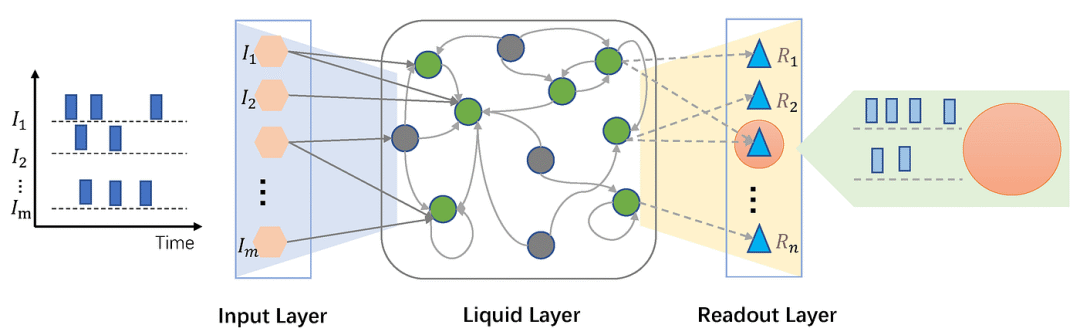
该首字母缩略词中的“流动liquid”部分来自网络对流动时间常数 (Liquid Time Constant,LTC) 的使用,这是一个输入相关项,可改变网络连接强度以适应新输入。LTC 是 LNN 在训练后能够适应新输入的原因。此外,流动时间常数以及节点的权重都是有界的。这意味着 LNN 不像传统 RNN 和其他连续时间循环架构那样容易受到梯度爆炸的影响。
与传统的时间序列预测框架相比,LNN 具有多项优势。首先也是最重要的就是其适应性。由于 LNN 具有“流动性”特性,因此它们可以在训练后改变自身以模拟新的分布https://tyagi-bhaumik.medium.com/liquid-neural-networks-revolutionizing-ai-with-dynamic-information-flow-30e27f1cc912。这种适应性使它们在处理数据分布变化和噪声过多的任务时非常有效。LNN 的稳健性也使它们可以在任务之间转移。
每个神经元的信息密度增加意味着小型 LNN 可以模拟复杂的行为,而这可能需要数万或数十万个传统节点才能模拟。例如,在一次演示该技术的 TED 演讲中https://www.youtube.com/watch?v=RI35E5ewBuI,Hasani仅使用 19 个 LNN 节点就能引导车辆。
这种尺寸缩小使 LNN 比传统神经网络更加透明https://www.techopedia.com/definition/liquid-neural-network。大型神经网络是黑匣子,因为它们的权重和节点太多,难以分析单个关系。通过缩小而不是扩大,节点和权重可以在上下文中进行解释,您不仅可以实现目标,还可以知道为什么这样做。
现在,让我们真正深入研究一下 LNN 的实际工作原理https://arxiv.org/abs/2006.04439。液态神经网络是神经 ODE 的演变,它使用一系列通过非线性互连门协调的一阶常微分方程 (Ordinary Differential Equations, ODE) 来模拟系统动力学。这与通过一系列隐式非线性 (激活函数) 表示系统的普通神经网络不同。ODE 能够模拟比典型激活函数复杂得多的行为,并以复杂性为代价为每个节点提供更强大的表达能力。典型神经 ODE 隐藏状态的导数可以表示为以下方程:
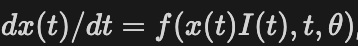
这里,f 是具有参数theta 的神经网络的输出,x(t)是当前状态,I(t)是时刻t的输入。求解这个微分方程可得出网络的下一个隐藏状态。重点在于,神经网络输出决定了隐藏状态的导数。这种设置有许多好处,例如易于确定因果关系、降低内存成本以及能够处理不规则间隔到达的数据。然而,它们也容易受到不稳定和梯度爆炸的影响,这可能会导致训练脱轨并使网络变得毫无用处。神经微分方程和其他连续时间循环架构在过去得到了广泛的应用,而 LNN 旨在借鉴它们的成功并解决它们的失败。
LNN 对线性 ODE 的封装略有不同,引入了液体时间常数 ( tau ) 和一个新的偏差参数:

原始神经 ODE 的影响显而易见。状态导数方程的两个主要组成部分仍然基于神经网络本身。包含时间常数的项和包含偏差的项相互抵消,有助于创建 LNN 的稳定行为特征。还请注意时间常数项如何直接作用于神经网络的隐藏状态,影响和限制节点之间权重的强度。
液体时间常数是一个有趣的术语,在 2020 年的论文中定义如下:

更新后的 LTC 等于之前的 LTC 除以 1,加上 LTC 乘以特定时间步长的神经网络输出。LTC“表征 ODE 的速度和耦合灵敏度”,本质上是一个常数项,它决定了各个节点之间的连接强度以及每个 ODE 节点的梯度的尖锐程度。由于 LTC 会随着输入而变化,因此 LNN 可以创建新的系统以适应输入随时间变化的新变化。
任何 ODE 求解器都可以对 LNN 进行前向传递,但在本文中,他们开发了自己的“融合”ODE 求解器,我不会详细探讨它。前向传递在以下伪代码中描述:
对于通过融合 ODE 求解器对 LNN 进行前向传递,求解器会离散化连续时间间隔,计算过渡状态,因此求解器的步骤不是连续的,而是从时间步骤 0 到 n 的一组离散步骤。实际的隐藏状态更新发生在以下等式中:

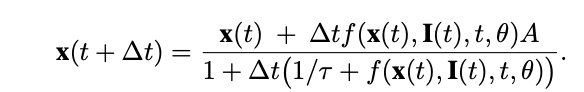
这里,下一个隐藏状态由当前隐藏状态加上神经网络的输出乘以时间变化和偏差项来确定。这是除以 1 加上变化时间乘以 1 除以 LTC 加上神经网络的输出。它实际上是定义 LNN 的方程,由时间变化加权,在伪代码中,它是针对网络中每个 T 个时间步骤的 N 个节点中的每一个节点计算的。
根据原始论文,当使用为 LNN 开发的融合 ODE 求解器时,长度为 T 的序列的时间复杂度为 O(L x T),其中 L 是所采取的离散化步骤数。这意味着具有 N 个单元的 LSTM 和具有 N 个神经元的 LNN 的前向传递时间复杂度相同。
训练 LNN 是通过时间反向传播 (Backpropagation Through Time, BPTT) 进行的,这是一种用于某些类型的循环神经网络架构的训练公式。它的工作原理是将网络在一系列时间状态上展开为一批前馈网络(本质上是一个非常长的前馈网络),然后汇总所有传递中的误差并使用它来更新每个时间步骤的权重。在 LNN 的上下文中,这意味着将一系列 ODE 求解器输出(展开网络的隐藏状态)打包为神经网络,然后执行 BPTT 过程来训练系统。
与其他连续架构相比,LNN 的主要吸引力之一是它的有界性,本文用状态稳定性定理对此进行了总结:

该定理规定,节点的状态由一组坐标决定,因为状态由 ODE 定义,所以它大于坐标(0,偏差向量中的最小量),小于坐标(0,偏差向量中的最大值)。因此,节点的状态是有界的,并且对未定义大小的输入具有鲁棒性。
所有这些主题的进一步阐述都可以在原始的液体时间常数网络论文https://arxiv.org/abs/2006.04439中找到。
LNN 比传统循环网络和其他时间连续网络具有许多优势,但它们也有缺陷。虽然 LNN 不受梯度爆炸的影响,但它们仍然容易受到长期依赖性梯度消失的影响,因此对于这些应用,明确保存长期依赖性 (LSTM) 的架构可能更有效。LNN 的准确性和效率受 ODE 求解器选择的影响,这是其实现和功效的另一个差异点。此外,与其他时间连续网络相比,它们的传递和训练速度较慢。然而,它们的表达能力、内存节省和透明度使 LNN 成为一个令人兴奋的研究领域,具有无数的应用。
参考文献
Abdulkader Helwan. (September 28, 2023). https://abdulkaderhelwan.medium.com/liquid-neural-networks-37ccaaee469a
Bhaumik Tyagi. (July 13, 2023). Liquid Neural Networks: Revolutionizing AI with Dynamic Information Flow. https://tyagi-bhaumik.medium.com/liquid-neural-networks-revolutionizing-ai-with-dynamic-information-flow-30e27f1cc912
Brian Heater. What is a liquid neural network, really? (August 17, 2023). https://techcrunch.com/2023/08/17/what-is-a-liquid-neural-network-really/
Daniel Ackerman. Liquid machine learning system adapts to changing conditions. (January 28, 2021). https://news.mit.edu/2021/machine-learning-adapts-0128
Ramin Hasani, Mathias Lechner, et. al. Liquid Time Constant Networks. (June 8, 2020) https://arxiv.org/abs/2006.04439
Ramin Hasani. (January 19, 2023). Liquid Neural Networks https://www.youtube.com/watch?v=RI35E5ewBuI
Tim Keary. (September 25, 2023). Liquid Neural Network (LNN) https://www.techopedia.com/definition/liquid-neural-network



内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢