
受物理启发的生成模型(例如扩散模型)构成了一个强大的生成模型家族。该家族模型的优势在于相对稳定的训练过程和高容量。仍有许多可能的改进。在论文中,我们将首先深入研究扩散模型中训练和采样的改进技术。当数据分布为多模态时,扩散模型的训练目标表现出高方差。为了缓解这种情况,我们提出了一个训练目标,该目标概括了传统的去噪分数匹配并显着降低了训练目标的方差。或者,我们引入了一个训练框架,将可学习的离散潜变量集成到连续扩散模型中。这些潜变量简化了扩散模型复杂的噪声到数据映射的学习。另一方面,扩散模型的采样过程通常涉及求解微分方程。为了加快采样过程,我们提出了一种新的采样算法,该算法结合了以前的 ODE 和 SDE 采样器的优点,大大提高了预训练扩散模型的性能。此外,我们的研究探索了通过在生成过程中引入相互排斥力来促进有限样本多样性的方法。在物理启发的生成模型领域,许多物理过程可用于开发生成模型。我们将介绍一种源自静电理论的新型生成模型系列,称为泊松流生成模型 (PFGM)。PFGM 可与领先的扩散模型相媲美,同时展示出改进的采样稳健性。扩展版本 PFGM++ 将扩散模型和 PFGM 置于同一框架下,并引入了新的、更好的模型。我们将进一步介绍一种将物理过程转化为生成模型的原则性方法。

论文题目:On Physics-Inspired Generative Models
作者:Yilun Xu
类型:2024年博士论文
学校:Massachusetts Institute of Technology(美国麻省理工学院)
下载链接:
链接: https://pan.baidu.com/s/1IToFFpLKRJPLO3aeJmTD4Q?pwd=b3yi
硕博论文汇总:
链接: https://pan.baidu.com/s/1Gv3R58pgUfHPu4PYFhCSJw?pwd=svp5


1.1 通过逆转物理过程进行生成建模
基于热力学的原理 [10],扩散模型涉及两个对立的过程:一个前向过程将数据分布逐渐转化为一个更简单的先验分布,另一个反向过程通过逐步去噪从该噪声先验分布中生成样本。扩散模型中的前向过程是一个简单的布朗运动,通过逐步增加高斯噪声来降解数据。为了逆转这一过程,只需学习一个时间依赖的向量场,即得分函数,并迭代求解一个微分方程 [22]。与GANs和VAEs不同,扩散模型的训练不需要多个神经网络之间的同步,从而使训练过程更加稳定。此外,它们在架构设计上不受限,采用类似于神经网络串联的迭代过程,从而增强了整体容量。这种稳定性和增强的容量使扩散模型能够有效扩展到大规模数据集。
尽管扩散模型具有诸多优势,但它们仍面临一些挑战,包括在处理多模态数据时高方差的训练过程,以及缓慢的迭代采样过程。此外,独立同分布(i.i.d.)的采样过程往往会导致重复的样本。这些问题强调了在复杂数据集上稳定和改进扩散模型训练方法的必要性,并且需要新技术来加速采样过程并提高小批量样本的多样性。此外,扩散模型只是众多物理启发生成模型之一。除布朗运动外,仍有许多物理过程尚未开发,可以用来构建生成模型。这引出了一个重要问题:我们能否发现其他物理启发的生成模型,它们展示出更好的性能?在接下来的部分中,我们将简要总结扩散模型的改进训练和采样技术,并讨论我们开发其他物理启发生成模型的研究,这些将在后续章节中详细阐述。
1.1.1 扩散模型的改进训练技术
扩散模型的训练利用了一种扰动-去噪方法来估计向量场。其过程是先通过高斯噪声扰动干净的数据,然后网络从这些扰动样本中重构原始数据 [12]。然而,对于复杂的多模态数据,许多干净的数据点可能被扰动为相似的噪声样本,导致训练目标不明确并引发不稳定性。
在文献 [23] 中,我们通过多个干净数据点的加权求和来估计真实目标,精确地指示从扰动样本到真实向量场的方向。该新颖的训练目标推广了传统的单点估计方法,显著减少了训练目标中的方差。因此,在各种扩散模型变体中,样本质量得到了提高,训练过程更加稳定,训练速度也得到了加快。
扩散模型面临的另一个挑战是,需要学习一个从单峰高斯分布到多峰数据分布的非线性且高度复杂的映射。这种复杂性增加了训练的难度,并导致生成常微分方程(ODE)[24] 轨迹呈现强烈的曲率。为解决这一问题,我们在扩散模型中引入了离散潜变量。这些离散潜变量有助于捕获数据分布中的不同模式,而扩散模型的任务则转变为基于给定的离散潜变量捕获每个模式内的连续变化。离散与连续变化的分离建模显著简化了模型复杂的噪声到数据映射的学习过程。这一方法有效降低了扩散模型生成ODE的曲率,尤其是在较大的扩散时间下,整体训练损失得到了减少。
1.1.2 扩散模型的改进采样技术
在扩散模型的采样过程中,求解微分方程通常涉及速度和质量之间的权衡。确定性采样器(基于ODE的)[25]–[27] 速度快,但性能达到平台期,而随机采样器(基于SDE的)[27]、[28] 样本质量更好,但速度较慢。我们的分析将这种差异归因于采样误差:ODE采样器的离散化误差较小,而SDE中的随机性会收缩采样过程中的累积误差 [29]。
基于这些见解,在文献 [29] 中,我们提出了一种名为Restart的新采样算法,该算法结合了ODE和SDE的优点。该方法在附加的前向步骤中加入大量噪声,并严格遵循逆ODE过程。前向噪声的引入增强了随机性的收缩效应,而逆ODE过程的遵循则加快了采样速度。这种将随机性和确定性采样过程分离的方法极为有效,Restart在标准基准(CIFAR-10和ImageNet-64)上超过了SDE和ODE采样器的速度和质量,并在大规模文本到图像的Stable Diffusion模型中展示了文本-图像对齐、视觉质量和多样性的卓越平衡。
传统上,扩散模型从模型分布中生成独立同分布的样本。然而,在实际操作中,模型通常需要多次采样以获得一组多样化的小批量样本,这会带来与采样时间无关的成本。我们提出超越独立样本假设,以提高样本的多样性和效率。我们的方法引入了一种扩展的基于扩散的生成采样方法,称为粒子引导。在这种方法中,联合粒子的时间演化势通过在样本(粒子)之间加入互斥力来强制多样性。根据实验结果,我们的框架在文本到图像生成和分子构象生成等应用中提高了样本的多样性并减轻了记忆效应。
1.1.3 基于其他物理过程的生成模型
以扩散模型为显著例子,物理启发的生成模型包含一个前向过程,该过程将复杂的数据分布简化为逐步的先验分布,随后通过一个反向过程(即采样过程)逐步将这些先验分布还原为原始数据分布。因此,为了定义新的物理启发生成模型,必须确定一个合适的前向过程。该过程应自然地随着时间简化数据分布,并且是可逆的,同时其相关的向量场应该易于被神经网络学习。
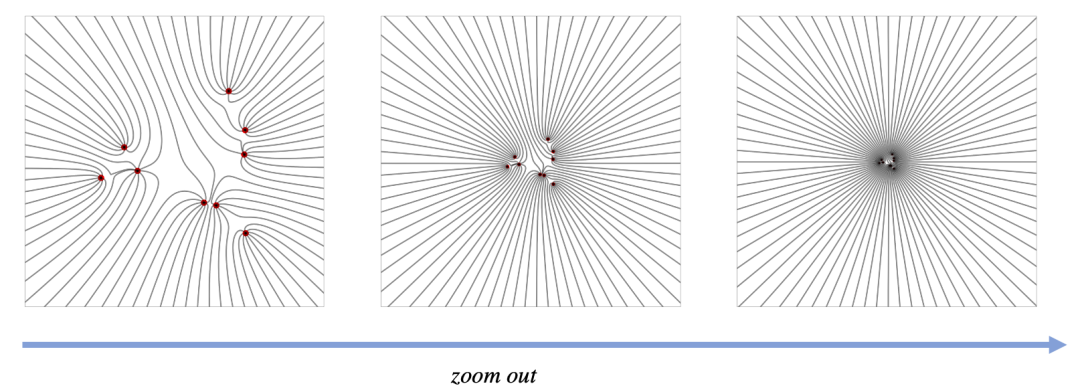 3D 增强空间中 2D 电场的逐渐缩小视图。随着与数据支持的距离增加,电荷分布逐渐类似于点电荷。这表明当我们距离足够远时,电荷分布实际上“塌陷”到一个点。
3D 增强空间中 2D 电场的逐渐缩小视图。随着与数据支持的距离增加,电荷分布逐渐类似于点电荷。这表明当我们距离足够远时,电荷分布实际上“塌陷”到一个点。
借助静电学原理,我们为物理启发的生成模型开辟了一条新路径,并介绍了泊松流生成模型(Poisson Flow Generative Models, PFGM)[30] 及其扩展版本PFGM++ [31]。PFGM将数据解释为增广空间中的电荷。如图1.1所示,当我们从数据支撑远离足够远时,电荷分布坍缩为一个点电荷,电场在各个方向上呈现辐射状。因此,可以证明这些电荷发出的电场线定义了数据分布和大半球上均匀分布之间的双射。实验结果表明,这一新模型家族在样本质量、采样速度和稳健性方面超越了扩散模型。此外,我们还探索了物理过程和生成模型之间的对偶性,旨在概念化和设计更多新的物理启发生成模型 [13]。
1.2 论文摘要
本论文分为三个主题部分。下面简要概述每个部分的内容。
第一部分 重点开发新技术,旨在稳定扩散模型的训练,并在处理复杂的多模态数据集时,优化生成轨迹。
第三章 我们通过引入参考批次来解决扩散模型目标中的高方差问题,并使用参考批次计算加权条件得分,作为更稳定的训练目标。我们展示了这一过程在具有挑战性的中间阶段中,通过减少训练目标协方差(的迹)确实起到了帮助作用。本章基于文献 [23]。
第四章 我们通过一个编码器推断可学习的离散潜变量,并对扩散模型和编码器进行端到端训练。离散潜变量通过降低扩散模型生成ODE的曲率,显著简化了其复杂的噪声到数据映射的学习过程,并通过ODE采样器提高了在各种数据集上的样本质量。本章基于文献 [32]。
第二部分 讨论了加速扩散模型采样过程的技术,以及通过施加样本之间的互斥力来促进多样性。所有讨论的技术都不需要重新训练,且可以直接应用于任何预训练的扩散模型。
第五章 我们提出了一种名为Restart的新采样算法,结合了先前ODE和SDE采样器的优势。Restart算法在附加的前向步骤中加入大量噪声,并严格遵循逆ODE过程。实验结果表明,Restart采样器在速度和精度上均超过了先前的SDE和ODE采样器。本章基于文献 [29]。
第六章 我们提出了粒子引导,一种扩展的基于扩散的生成采样方法,其中通过一个联合粒子的时间演化势来强制样本多样性。在条件图像生成中,我们测试了该框架,并证明其在不影响质量的情况下增加了多样性;在分子构象生成中,我们改进了相较于先前方法的中位误差。本章基于文献 [33]。
第三部分 探讨了一类新型的生成模型,这些模型基于静电理论,并与扩散模型在扩展视角下进行了统一。本部分还展望了通过物理过程构建生成模型的方法论。
第七章 我们介绍了一种新型生成模型——泊松流生成模型(PFGM),基于静电理论。我们将数据点解释为增广空间中 z=0 超平面上的电荷,生成一个高维电场(泊松方程解的梯度)。我们证明了,如果这些电荷沿电场线向上流动,它们在 z=0 平面的初始分布会转化为半径为 r 的半球上的分布,并且在 r → ∞ 时变得均匀。我们展示了PFGM在图像生成速度上提供了比先前最先进扩散模型更好的性能。本章基于文献 [30]。
第八章 我们扩展了PFGM中使用的静电理论,将扩散模型与PFGM统一起来。更有趣的是,在两者之间的插值揭示了一个性能最优的新平衡点,达到了图像生成的新标杆性能。我们为为什么PFGM和扩散模型都是次优解提供了理论解释。本章基于文献 [31]。
第九章 我们提出了一个统一的框架和算法,将物理过程转化为平滑的密度流生成模型。此外,我们基于底层物理偏微分方程(PDE)的色散关系,提出了一种分类标准。这种理论方法可应用于各种物理PDE,从而发现新的生成模型家族。
第十章 我们总结了论文内容并讨论了当前的局限性。
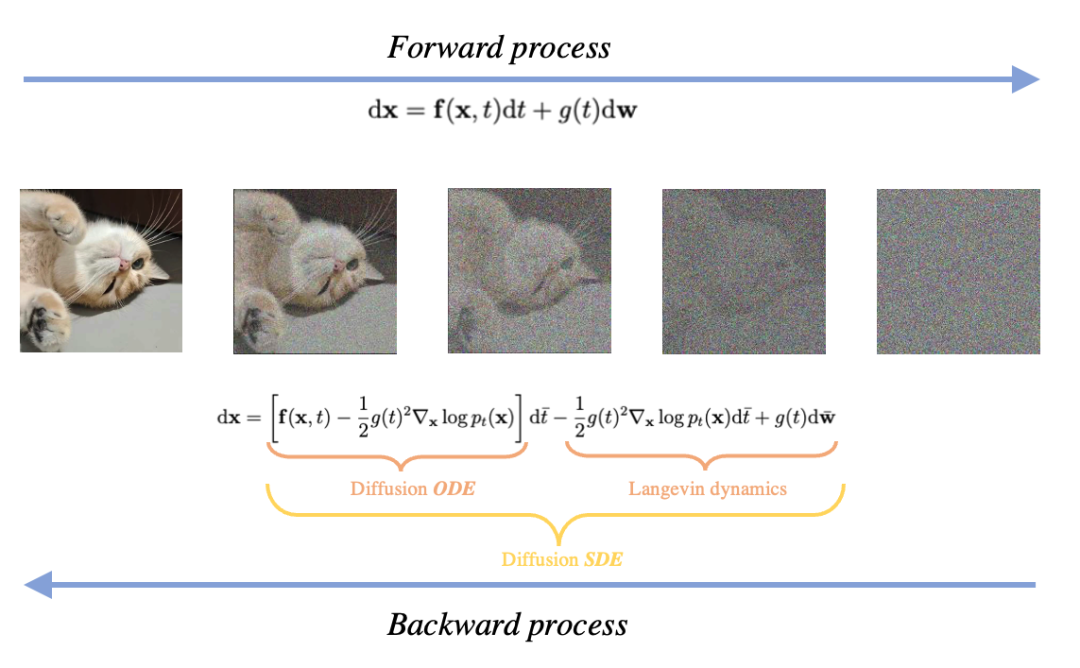 扩散模型中的前向 SDE 和后向 SDE/ODE。
扩散模型中的前向 SDE 和后向 SDE/ODE。
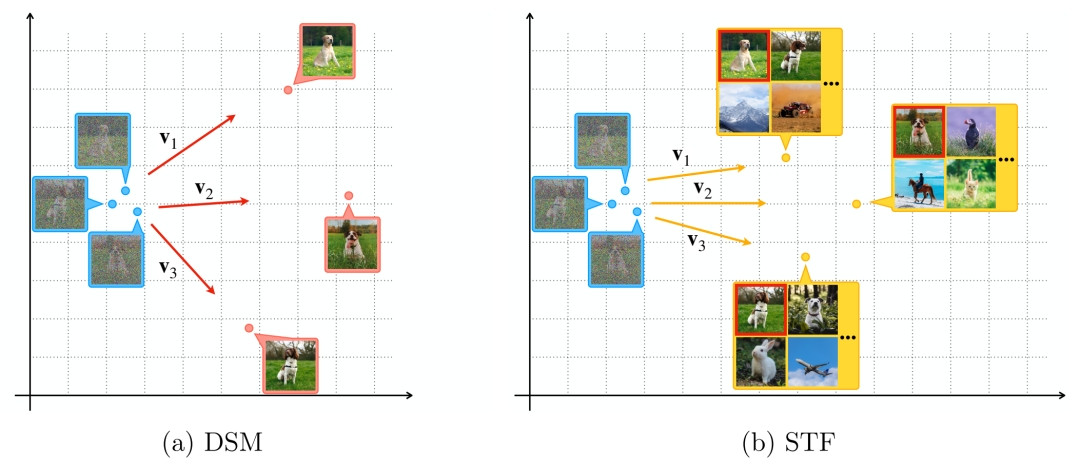 说明 DSM 目标与我们提出的 STF 目标之间的差异。“被破坏”的图像(蓝色框中)彼此接近,而它们的源(红色框中)则不然。尽管期望中的真实分数是 vi 的加权平均值,但 DSM 目标的单独训练更新具有很高的方差,我们的 STF 目标通过包含大参考批次(黄色框)显着降低了方差。
说明 DSM 目标与我们提出的 STF 目标之间的差异。“被破坏”的图像(蓝色框中)彼此接近,而它们的源(红色框中)则不然。尽管期望中的真实分数是 vi 的加权平均值,但 DSM 目标的单独训练更新具有很高的方差,我们的 STF 目标通过包含大参考批次(黄色框)显着降低了方差。
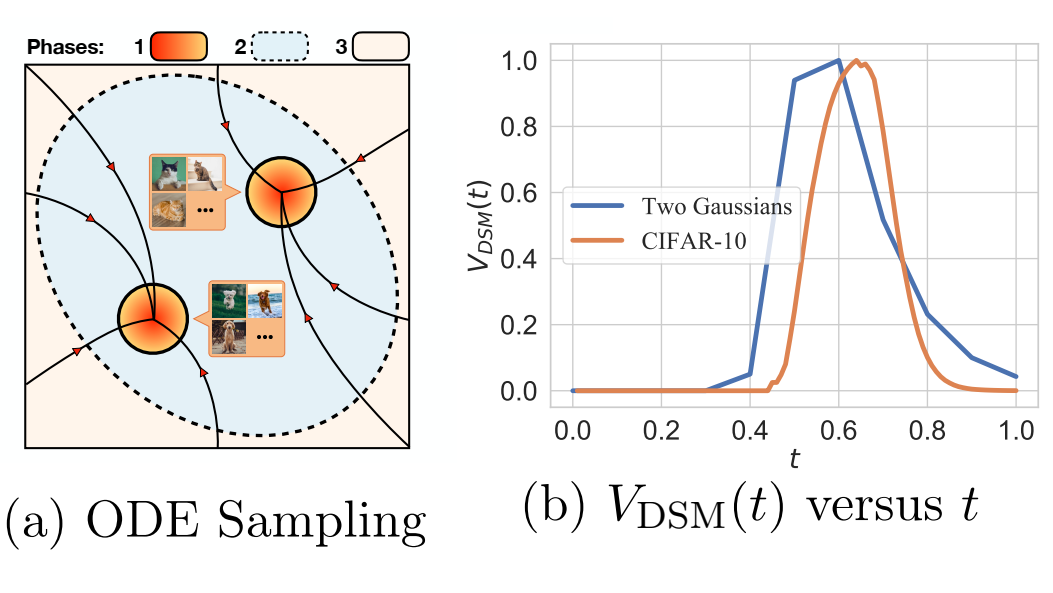 (a):二模分布中的三个阶段的图示。(b):两个分布的估计 VDSM(t)。出于说明目的,我们将最大值标准化为 1。
(a):二模分布中的三个阶段的图示。(b):两个分布的估计 VDSM(t)。出于说明目的,我们将最大值标准化为 1。
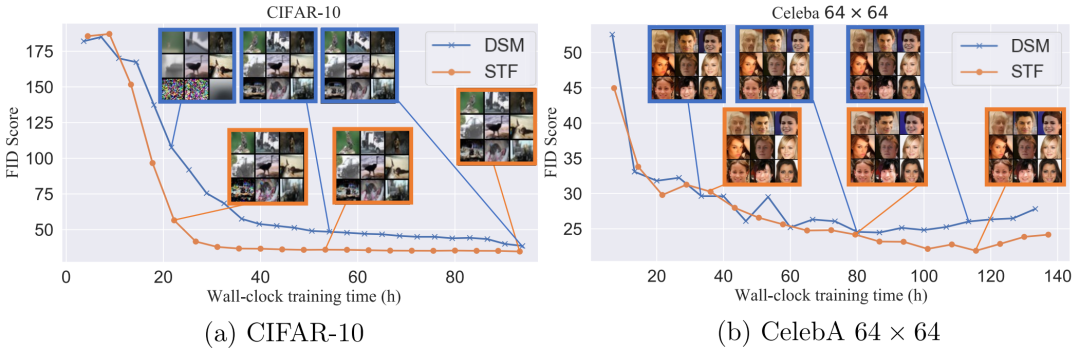 FID 和在 (a) CIFAR-10 和 (b) CelebA 64^2 上的整个训练过程中生成的样本
FID 和在 (a) CIFAR-10 和 (b) CelebA 64^2 上的整个训练过程中生成的样本
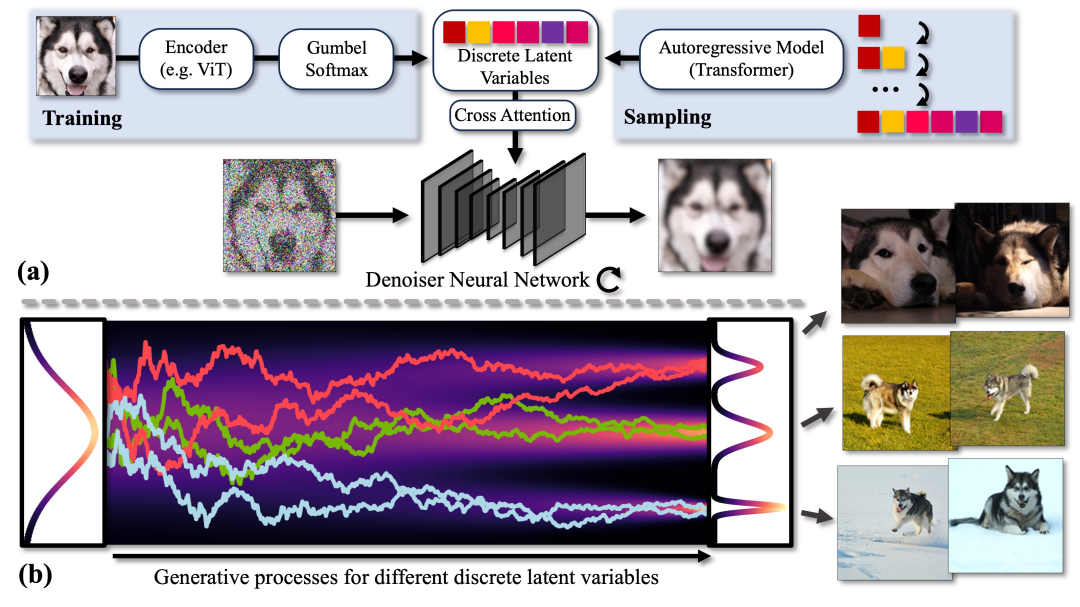 离散连续潜在变量扩散模型 (DisCo-Diff) 通过捕获全局外观模式的附加离散潜在变量来增强 DM,此处显示的是哈士奇的图像。(a) 在训练过程中,通过编码器推断视觉变换器图像的离散潜伏[69],并通过交叉注意将其馈送到 DM。Gumbel-Softmax 分布的连续松弛促进了反向传播。为了对新图像进行采样,在离散潜在变量的分布上学习了一个额外的自回归模型。(b) 生成式去噪扩散轨迹的可视化示意图。不同的颜色表示不同的离散潜在变量,将轨迹推向不同的模式。
离散连续潜在变量扩散模型 (DisCo-Diff) 通过捕获全局外观模式的附加离散潜在变量来增强 DM,此处显示的是哈士奇的图像。(a) 在训练过程中,通过编码器推断视觉变换器图像的离散潜伏[69],并通过交叉注意将其馈送到 DM。Gumbel-Softmax 分布的连续松弛促进了反向传播。为了对新图像进行采样,在离散潜在变量的分布上学习了一个额外的自回归模型。(b) 生成式去噪扩散轨迹的可视化示意图。不同的颜色表示不同的离散潜在变量,将轨迹推向不同的模式。
 在 ImageNet 数据集上训练的 DisCo-Diff 生成的样本:(a) 随机采样的离散潜在变量和类标签;(b) 每个网格中的样本共享相同的离散潜在变量。顶/底行的类标签固定为咖啡壶/雪橇犬。
在 ImageNet 数据集上训练的 DisCo-Diff 生成的样本:(a) 随机采样的离散潜在变量和类标签;(b) 每个网格中的样本共享相同的离散潜在变量。顶/底行的类标签固定为咖啡壶/雪橇犬。
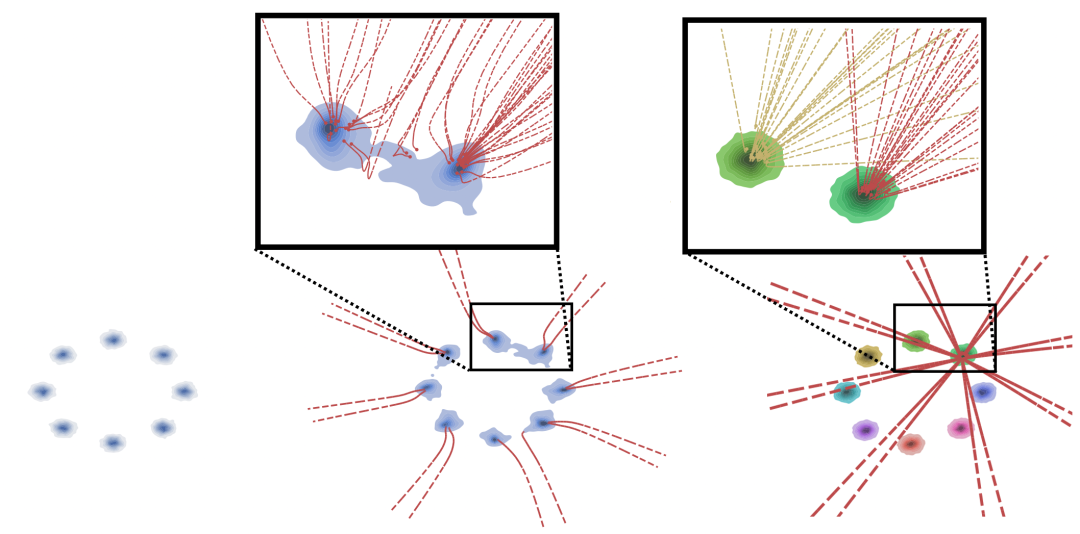 对高斯的二维混合建模。左:数据分布。中:由常规 DM 生成的数据。右:由 DisCo-Diff 生成的数据。我们使用不同的颜色来区分不同离散潜在变量生成的数据。我们进一步提供放大并通过虚线可视化一些 ODE 轨迹。
对高斯的二维混合建模。左:数据分布。中:由常规 DM 生成的数据。右:由 DisCo-Diff 生成的数据。我们使用不同的颜色来区分不同离散潜在变量生成的数据。我们进一步提供放大并通过虚线可视化一些 ODE 轨迹。
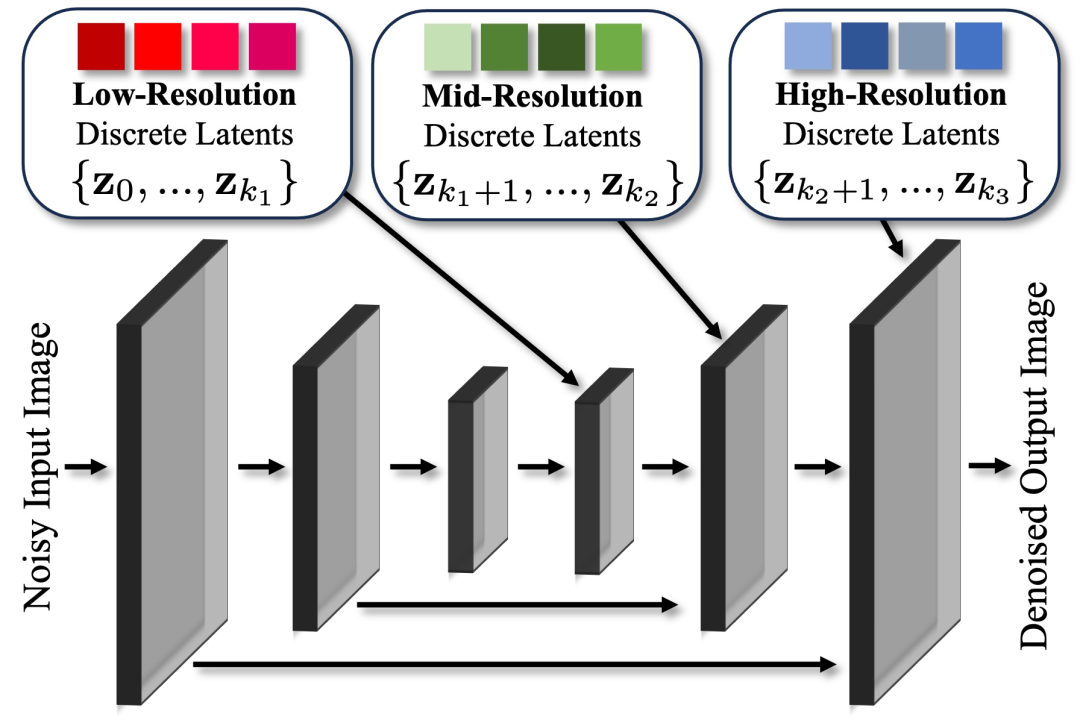 组分层 DisCo-Diff。不同的离散潜在特征以不同的特征分辨率馈送到降噪器 U-Net。
组分层 DisCo-Diff。不同的离散潜在特征以不同的特征分辨率馈送到降噪器 U-Net。
 上图:由两个 30 维离散潜在 z 和 z^ 创建的图像,最右侧的列组合了它们的子坐标。底部:通过固定 z 部分(源自红框图像)而产生的图像变化。我们看到较低分辨率的潜在因素会影响布局/形状;高分辨率潜伏改变颜色/纹理。
上图:由两个 30 维离散潜在 z 和 z^ 创建的图像,最右侧的列组合了它们的子坐标。底部:通过固定 z 部分(源自红框图像)而产生的图像变化。我们看到较低分辨率的潜在因素会影响布局/形状;高分辨率潜伏改变颜色/纹理。
 左:损失与时间。右图:采样过程中离散潜在切换的影响。这些数字代表总采样步骤的百分比。蓝色/绿色箭头表示利用与图中最左/最右网格相关的离散潜在变量的采样步骤。
左:损失与时间。右图:采样过程中离散潜在切换的影响。这些数字代表总采样步骤的百分比。蓝色/绿色箭头表示利用与图中最左/最右网格相关的离散潜在变量的采样步骤。
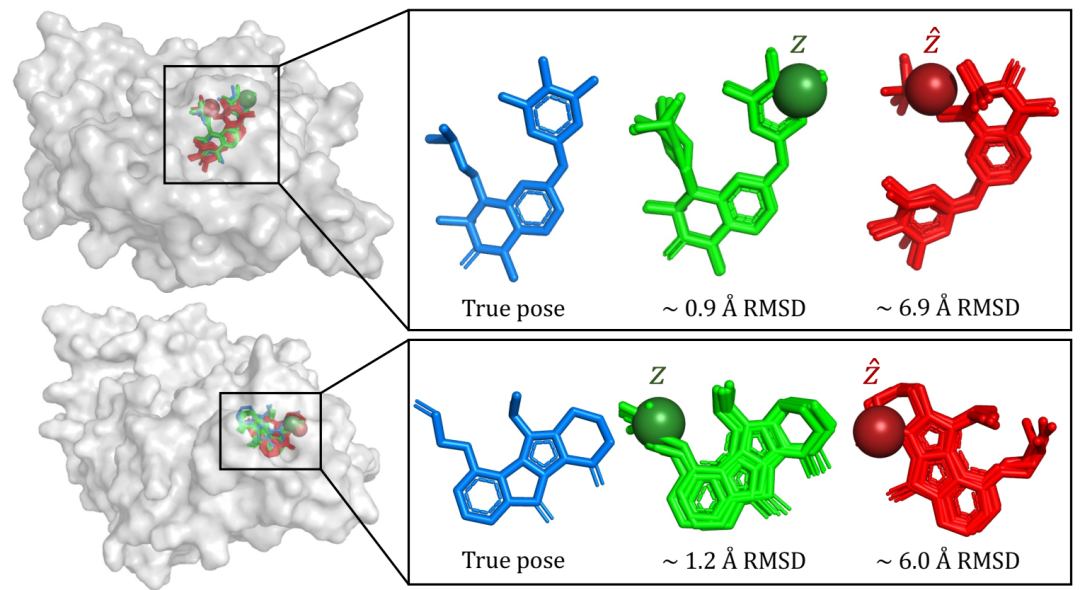 在不同的离散潜伏、“正确的”z(即与编码器相同)和不正确的 zˆ 条件下建模时建模的替代对接姿势的示例。DM 将它们映射到两组不同的合理方向,配体可以通过这些方向安装在口袋中值得注意的是,正确的潜在变量对应于真实值 2Å 以内的位姿。彩色珠子设置在与第一个潜在变量相对应的原子上。
在不同的离散潜伏、“正确的”z(即与编码器相同)和不正确的 zˆ 条件下建模时建模的替代对接姿势的示例。DM 将它们映射到两组不同的合理方向,配体可以通过这些方向安装在口袋中值得注意的是,正确的潜在变量对应于真实值 2Å 以内的位姿。彩色珠子设置在与第一个潜在变量相对应的原子上。
 在 DisCo-Diff 中生成样本,cfg 范围从 0 到 8,在 ImageNet-128 上的类标签“malamute”下。
在 DisCo-Diff 中生成样本,cfg 范围从 0 到 8,在 ImageNet-128 上的类标签“malamute”下。
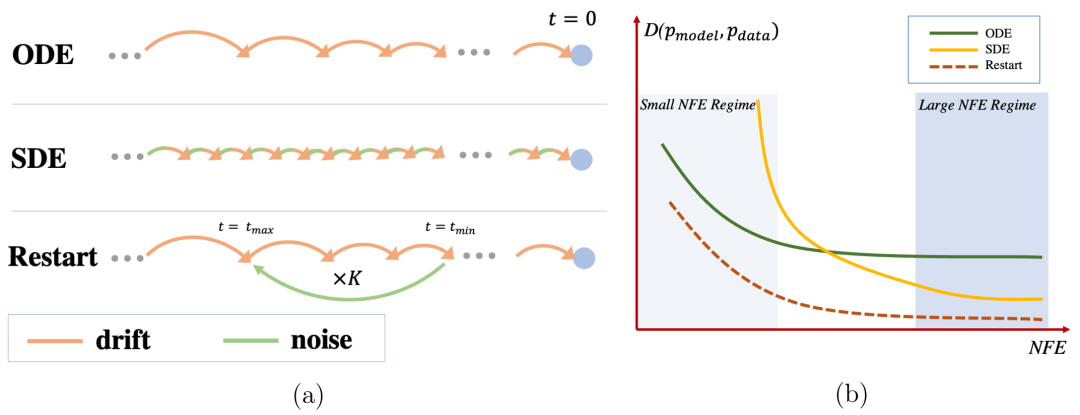 (a) 说明 ODE、SDE 和 Restart 中漂移和噪声项的实现。(b) 不同方法的样本质量与功能评估 (NFE) 数量的关系。ODE(绿色)提供快速速度,但即使具有较大的 NFE,也只能达到平庸的质量。SDE(黄色)获得了良好的样本质量,但需要大量的采样时间。与拥有自己获胜区域的 ODE 和 SDE 相比,Restart(红色)在所有 NFE 中实现了最佳质量。
(a) 说明 ODE、SDE 和 Restart 中漂移和噪声项的实现。(b) 不同方法的样本质量与功能评估 (NFE) 数量的关系。ODE(绿色)提供快速速度,但即使具有较大的 NFE,也只能达到平庸的质量。SDE(黄色)获得了良好的样本质量,但需要大量的采样时间。与拥有自己获胜区域的 ODE 和 SDE 相比,Restart(红色)在所有 NFE 中实现了最佳质量。
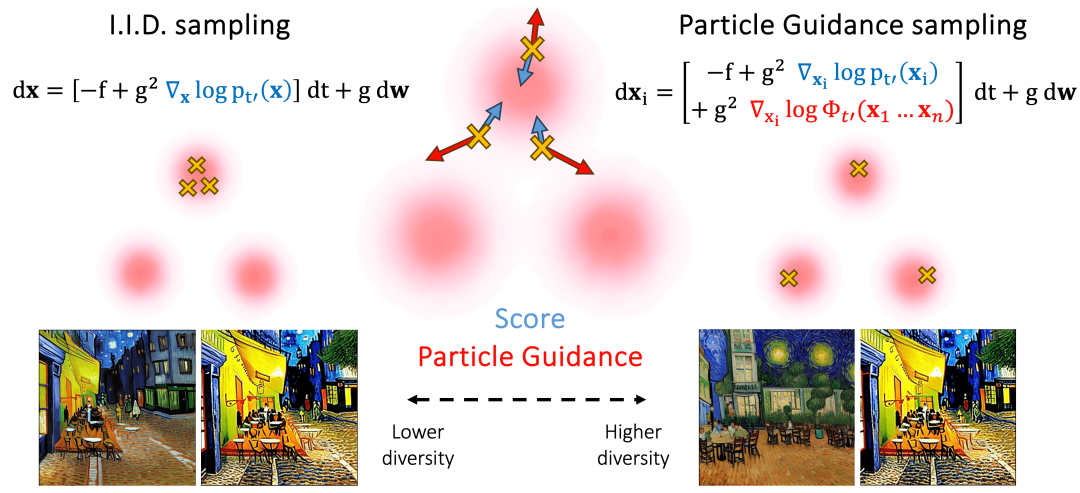 I.I.D 的比较和粒子引导采样。中心图代表每个步骤,粉红色的分布和黄色十字的样本,其中粒子引导不仅使用分数(蓝色),还使用联合电位(红色)的引导,导致它发现不同的模式(右侧样本与左侧样本)。在底部,梵高咖啡馆对使用和不使用粒子引导的稳定扩散生成的样本进行了成像。关于 I.I.D 次优性的更详细讨论抽样见附录 B.4.1。
I.I.D 的比较和粒子引导采样。中心图代表每个步骤,粉红色的分布和黄色十字的样本,其中粒子引导不仅使用分数(蓝色),还使用联合电位(红色)的引导,导致它发现不同的模式(右侧样本与左侧样本)。在底部,梵高咖啡馆对使用和不使用粒子引导的稳定扩散生成的样本进行了成像。关于 I.I.D 次优性的更详细讨论抽样见附录 B.4.1。
 文字提示:(a,b)“一个宝宝在吃蛋糕,脖子上系着领带,背景是气球”(COCO);(c,d,e)“VAN GOGH CAFE TERASSE copy.jpg”,带原始训练数据来自(c)。
文字提示:(a,b)“一个宝宝在吃蛋糕,脖子上系着领带,背景是气球”(COCO);(c,d,e)“VAN GOGH CAFE TERASSE copy.jpg”,带原始训练数据来自(c)。
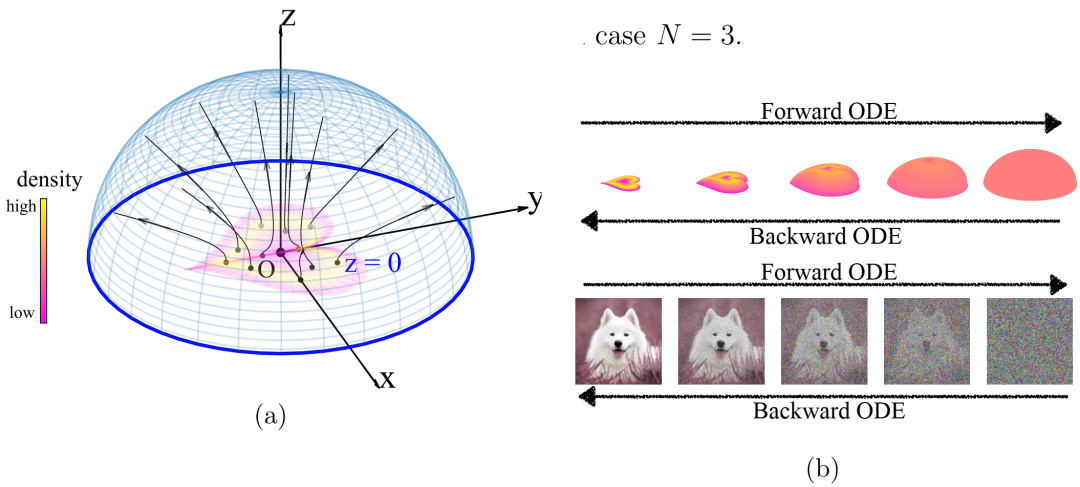 (a) 心形分布的 3D 泊松场轨迹 (b) 与泊松场有关的前向/后向 ODE 的分布(顶部)或(增强)样本(底部)的演变。
(a) 心形分布的 3D 泊松场轨迹 (b) 与泊松场有关的前向/后向 ODE 的分布(顶部)或(增强)样本(底部)的演变。
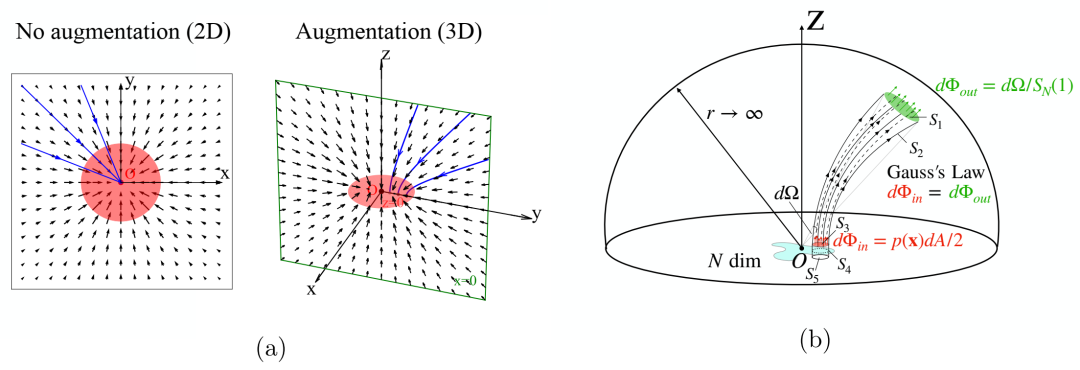 (a) 二维均匀圆盘(红色)的泊松场(黑色箭头)和粒子轨迹(蓝线)。左(无增强,二维):所有粒子塌陷到圆盘中心。右图(增强,3D):粒子撞击圆盘上的不同点。(b) 定理6的证明思想。根据高斯定律,流出通量dΦout等于流入通量dΦin。p(x)dA/2 中的因子 2 是由于 z < 0 和 z > 0 中泊松场的对称性所致。
(a) 二维均匀圆盘(红色)的泊松场(黑色箭头)和粒子轨迹(蓝线)。左(无增强,二维):所有粒子塌陷到圆盘中心。右图(增强,3D):粒子撞击圆盘上的不同点。(b) 定理6的证明思想。根据高斯定律,流出通量dΦout等于流入通量dΦin。p(x)dA/2 中的因子 2 是由于 z < 0 和 z > 0 中泊松场的对称性所致。
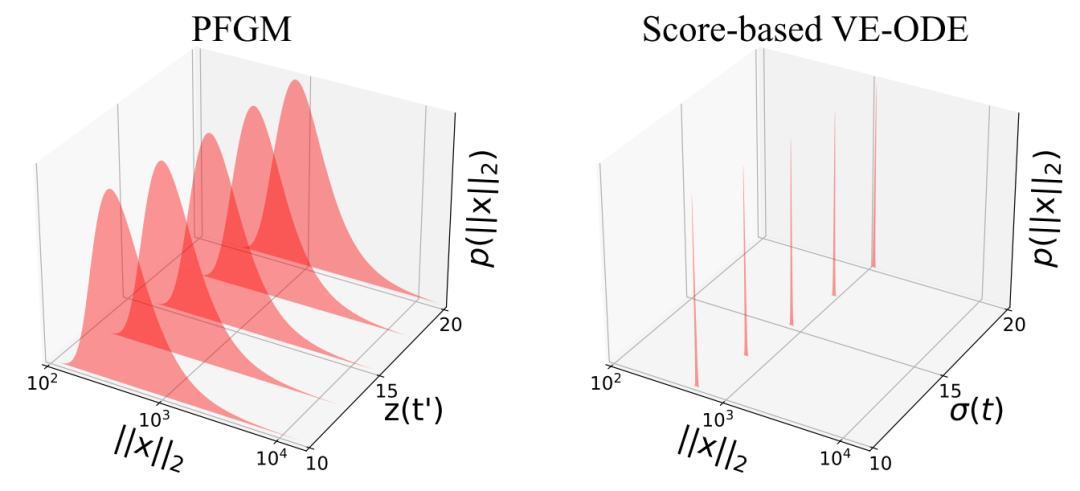
具有不同时间变量的范数分布样本(VE-ODE 为 σ,VE-ODE 为 z)PFGM)
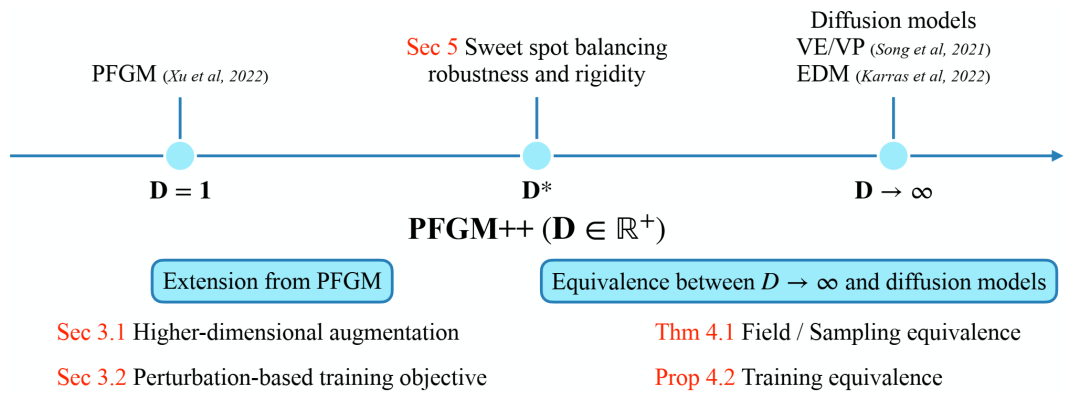 论文贡献和结构概述。PFGM++ 统一了 PFGM 和扩散模型,以及结合它们的优势(稳健性和刚性)的潜力。
论文贡献和结构概述。PFGM++ 统一了 PFGM 和扩散模型,以及结合它们的优势(稳健性和刚性)的潜力。
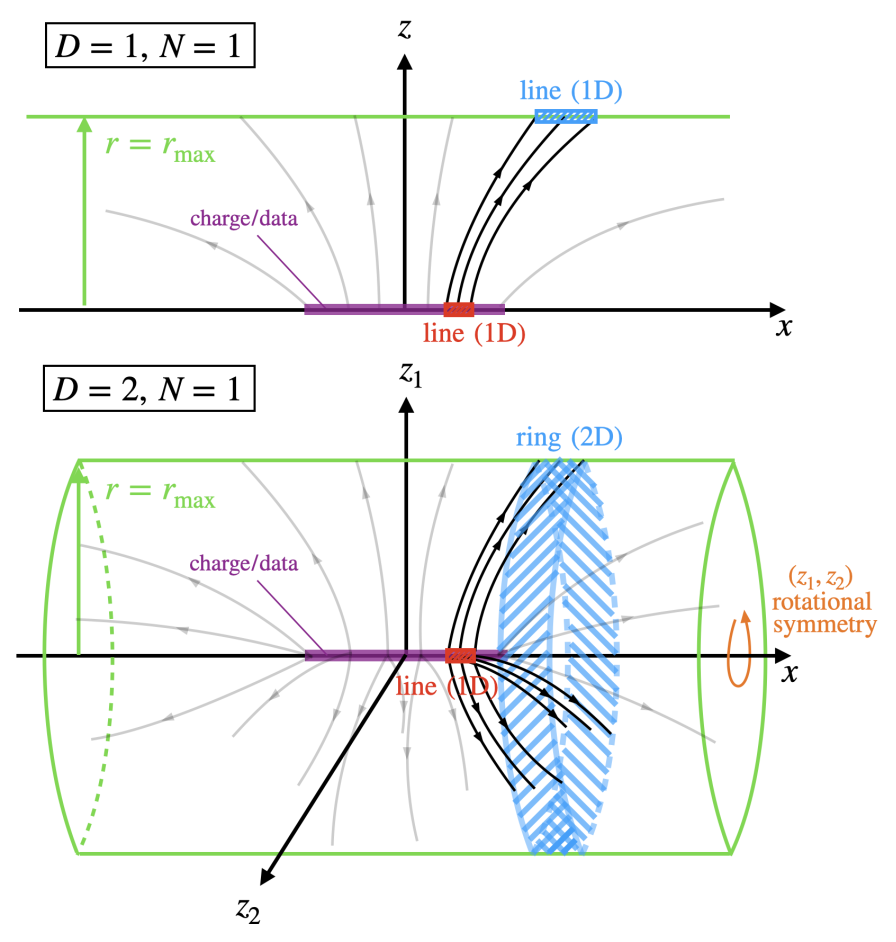 增强尺寸 D 会影响电场线(灰色),该电场线将线(紫色)上的电荷/数据连接到潜在空间(绿色)。当 D = 1(顶部)或 D = 2(底部)时,电场线分别将相同的红色线段映射到蓝色线段或蓝色环上。由电力线定义的映射在 z21 + z22 = r2 圆柱体的表面上具有 SO(2) 对称性。
增强尺寸 D 会影响电场线(灰色),该电场线将线(紫色)上的电荷/数据连接到潜在空间(绿色)。当 D = 1(顶部)或 D = 2(底部)时,电场线分别将相同的红色线段映射到蓝色线段或蓝色环上。由电力线定义的映射在 z21 + z22 = r2 圆柱体的表面上具有 SO(2) 对称性。
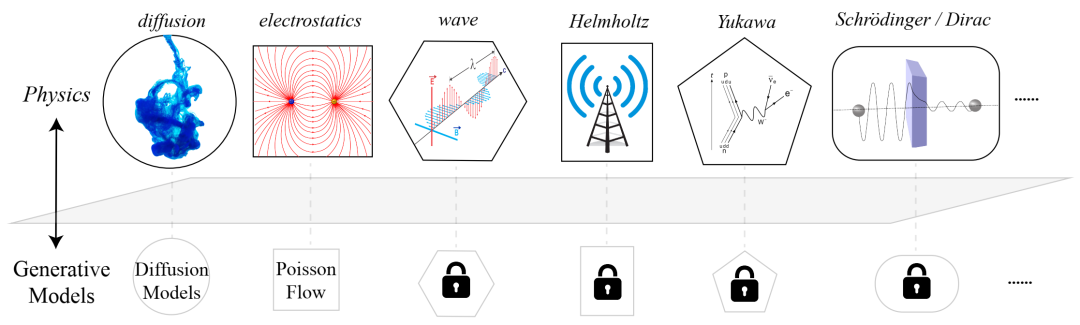 物理学和生成模型之间的二元性。到目前为止,研究人员只发现了扩散模型和泊松流。我们可以解锁更多吗?
物理学和生成模型之间的二元性。到目前为止,研究人员只发现了扩散模型和泊松流。我们可以解锁更多吗?
 将物理过程转换为生成模型的框架。
将物理过程转换为生成模型的框架。
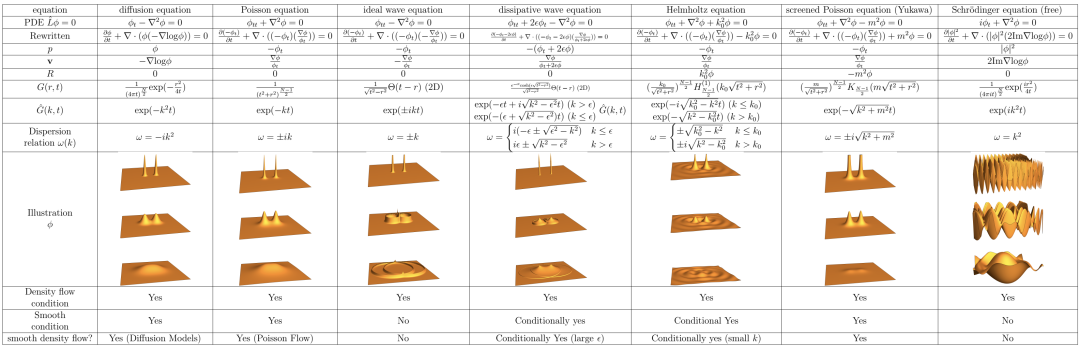 不同物理方程的结果、它们的性质以及它们是否可以转换为生成模型的摘要。x′和x分别为源点和场点,r == |x − x′|。
不同物理方程的结果、它们的性质以及它们是否可以转换为生成模型的摘要。x′和x分别为源点和场点,r == |x − x′|。
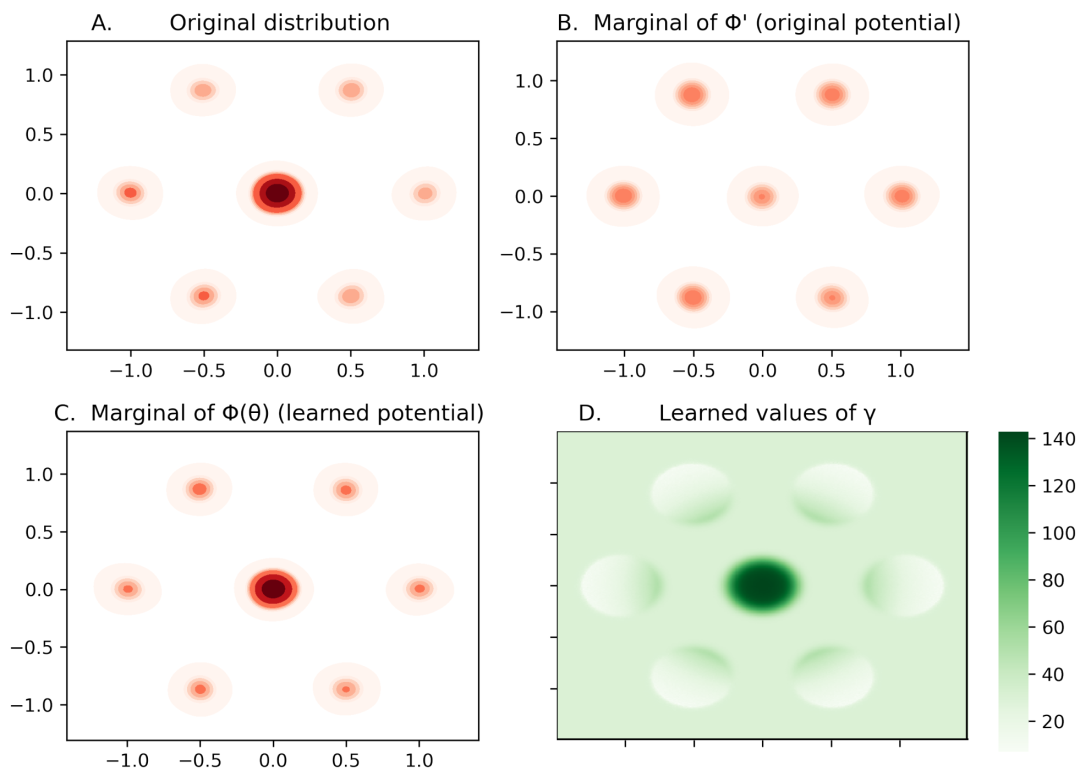 学习保留边际分布的势的综合实验。每个图的描述可以在文本中找到。
学习保留边际分布的势的综合实验。每个图的描述可以在文本中找到。
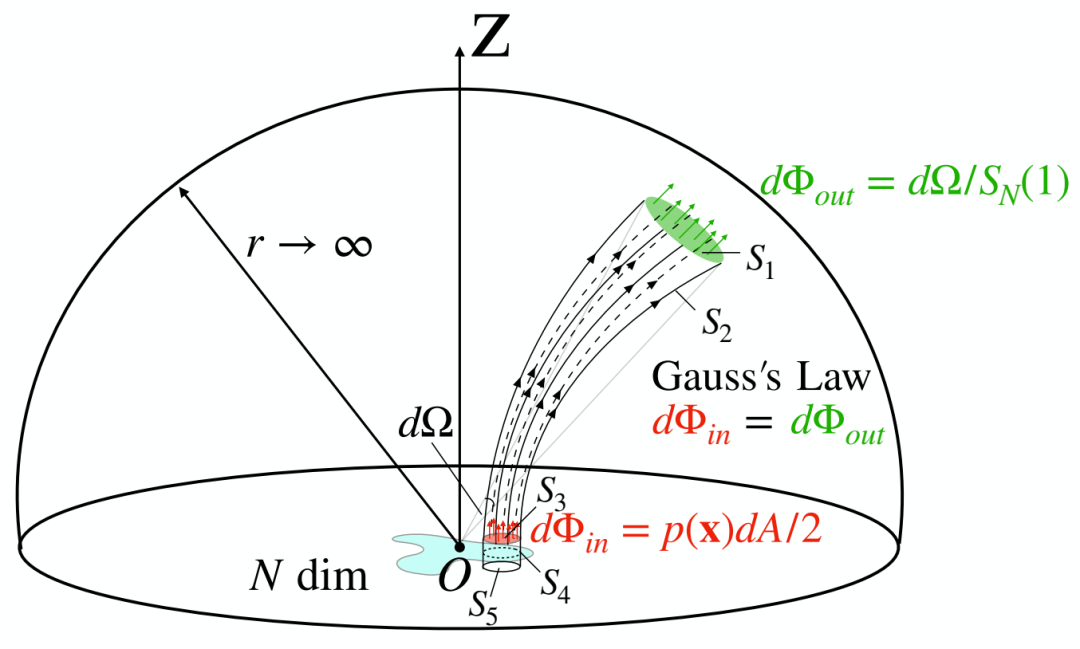 定理11的证明思想。根据高斯定律,流出通量dΦout等于流入通量dΦin。p(x)dA/2 中的因子 2 是由于 z < 0 和 z > 0 中泊松场的对称性所致。
定理11的证明思想。根据高斯定律,流出通量dΦout等于流入通量dΦin。p(x)dA/2 中的因子 2 是由于 z < 0 和 z > 0 中泊松场的对称性所致。
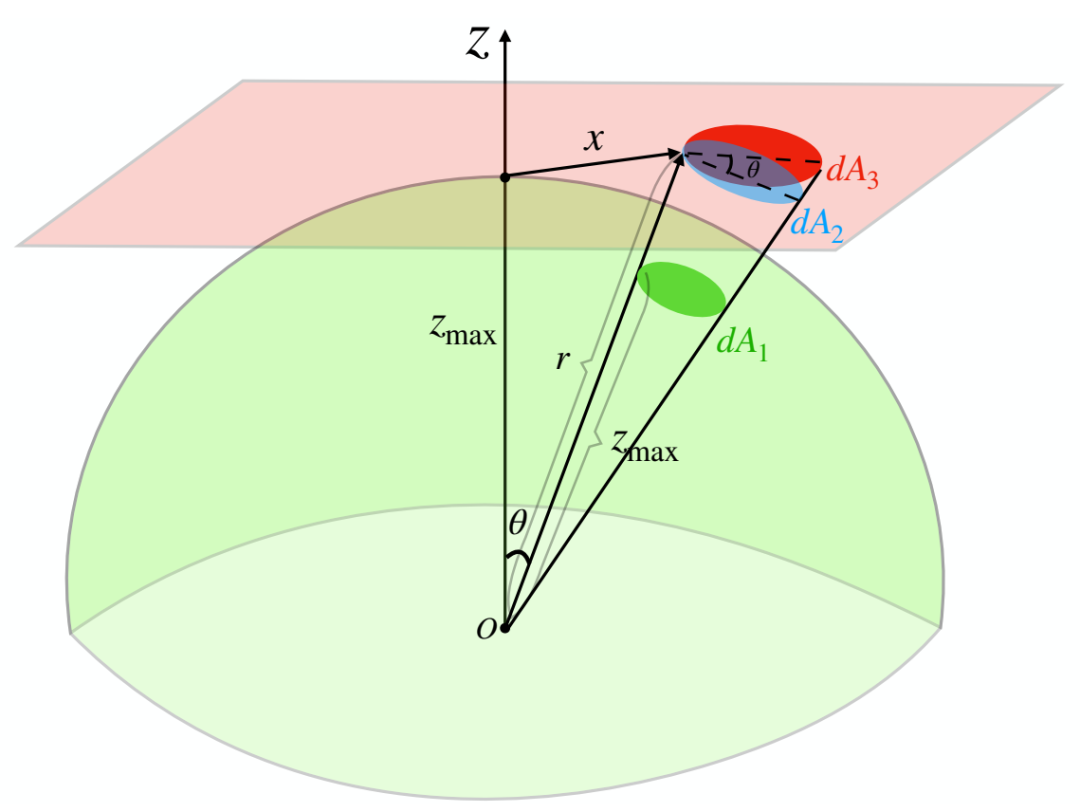 命题6的偏差图
命题6的偏差图
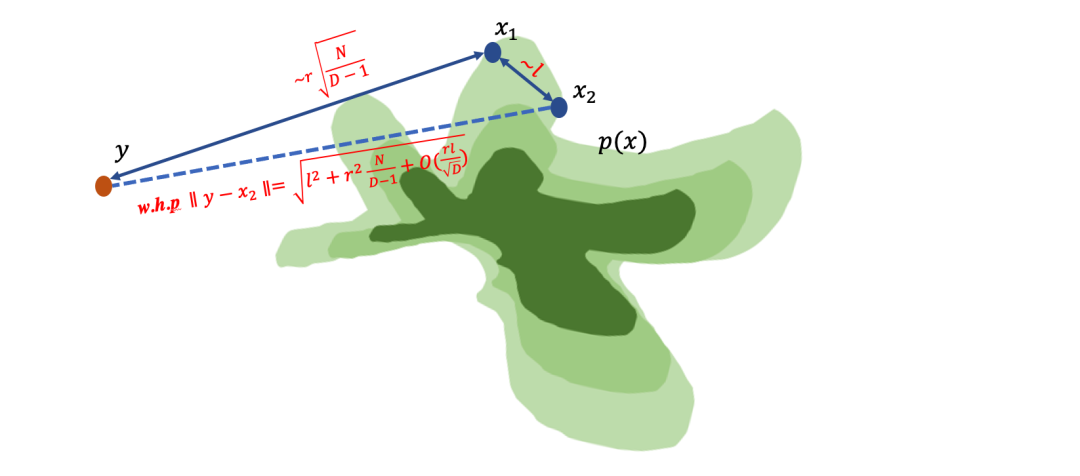 相位对准分析图解
相位对准分析图解









内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢