
新智元报道
新智元报道
【新智元导读】最近,陶哲轩向广大网友和数学爱好者发起了挑战:大众数学爱好者、证明助理、自动化助手和AI联合起来,是否可以证明扩展几个数量级的数学问题?

AI辅助证明数学研究,越来越可行了
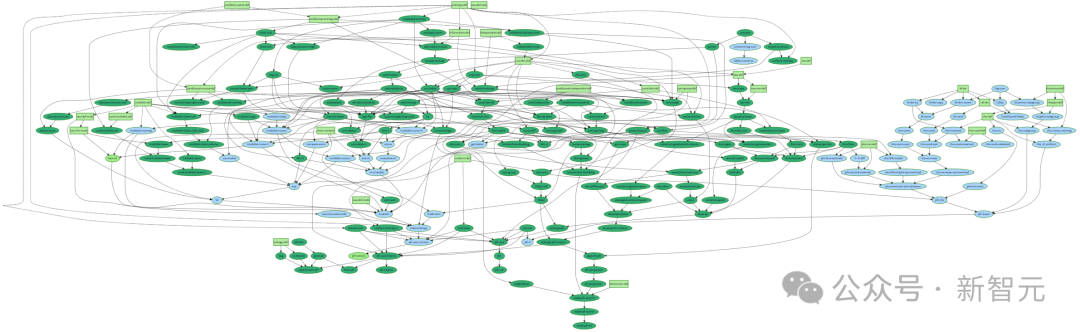

探索全新数学问题,成为可能


陶哲轩提出新项目
为此,陶哲轩自己也提出了一个项目,来进一步测试这一范式。 这个项目受到去年MathOverflow问题的启发。 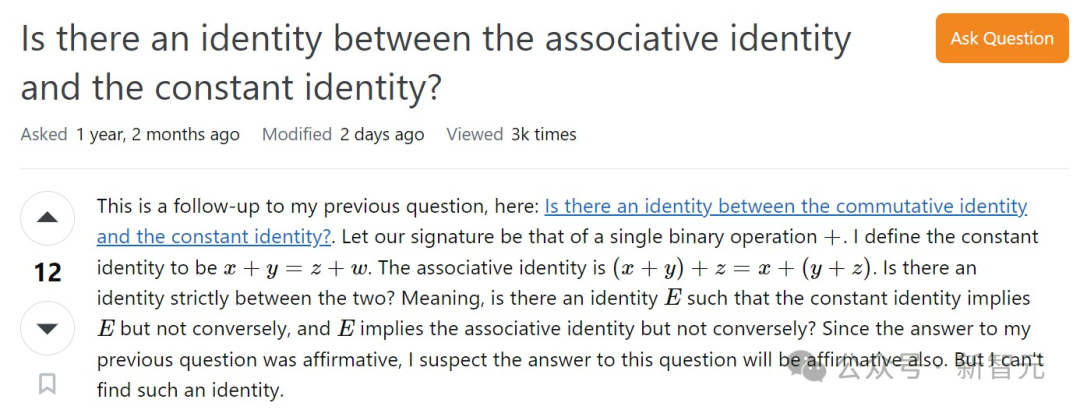
不久后,陶哲轩在自己的Mathstodon上,对它进行了进一步讨论。 
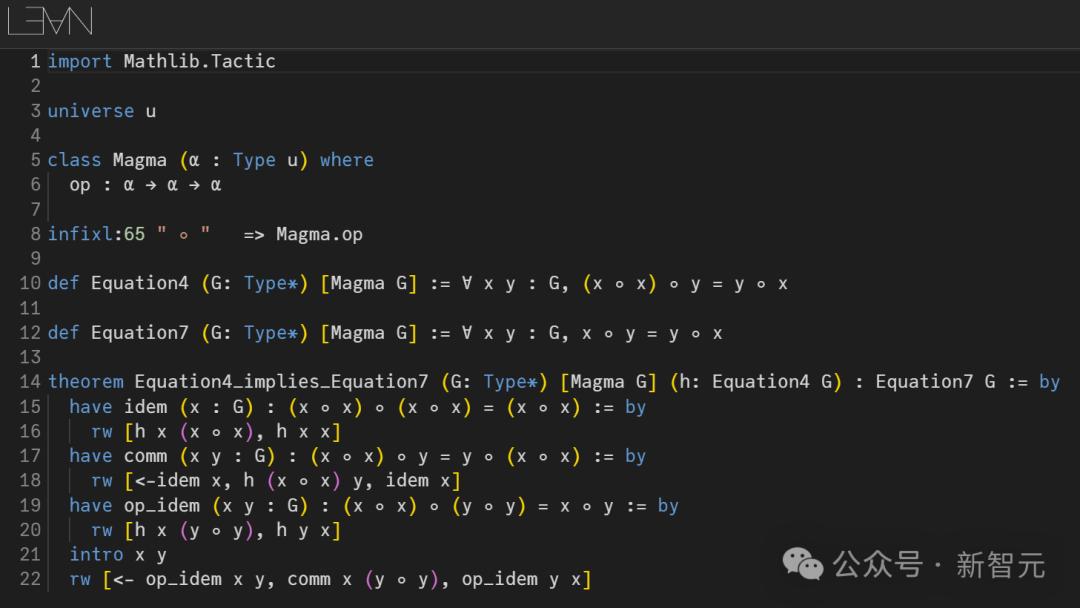
这个问题属于泛代数(universal algebra)领域,涉及对原群(magma)的简单等式理论的中等规模探索。 原群是一个配备了二元运算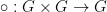 的集合G。
的集合G。 最初,这个运算o没有附加任何额外的公理,因此原群本身是较为简单的结构。 当然,通过添加额外的公理,如恒等公理或结合律公理,我们可以得到更熟悉的数学对象,例如群、半群或幺半群。 在这里,我们感兴趣的是(无常数的)等式公理。这些公理涉及由运算o和G中的一个或多个未知变量构建的表达式的相等性。 此类公理的两个熟悉的例子,是交换律x o y = y o x和结合律(x o y) o z = x o (y o z)。 其中x,y,z是原群G中的未知变量。 另一方面,(左)恒等公理e o x = x在这里不被视为等式公理(equational axiom),因为它涉及一个常数e ∈ G。这类涉及常数的公理在本研究中不予讨论。 接下来,为了阐明自己发起的研究项目,陶哲轩介绍了十一个关于原群的等式公理例子。 这些等式公理是仅涉及原群运算和未知变量的等式—— 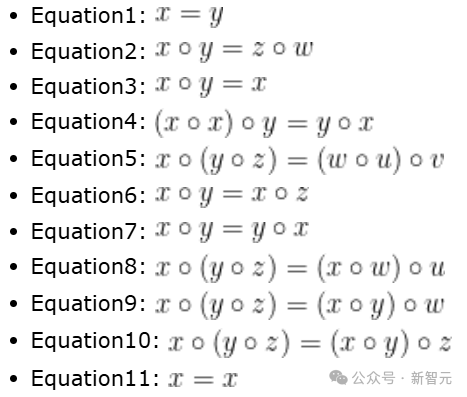
因此,举例来说,等式7表示交换律公理,而等式10表示结合律公理。 常数公理等式1是最强的,因为它限制了原群G最多只能有一个元素;与之相反,自反公理等式11是最弱的,所有原群都满足这一公理。 接下来,我们就可以探讨这些公理之间的推导关系:哪些公理能推出哪些公理? 例如,等式1可以推导出这个列表中的所有其他公理,而这些公理又可以推导出等式11。 等式8作为特殊情况可以推导出等式9,而等式9又作为特殊情况可以推导出等式10。 这些公理之间完整的推导关系可以用以下哈斯图(Hasse diagram)来描述: 
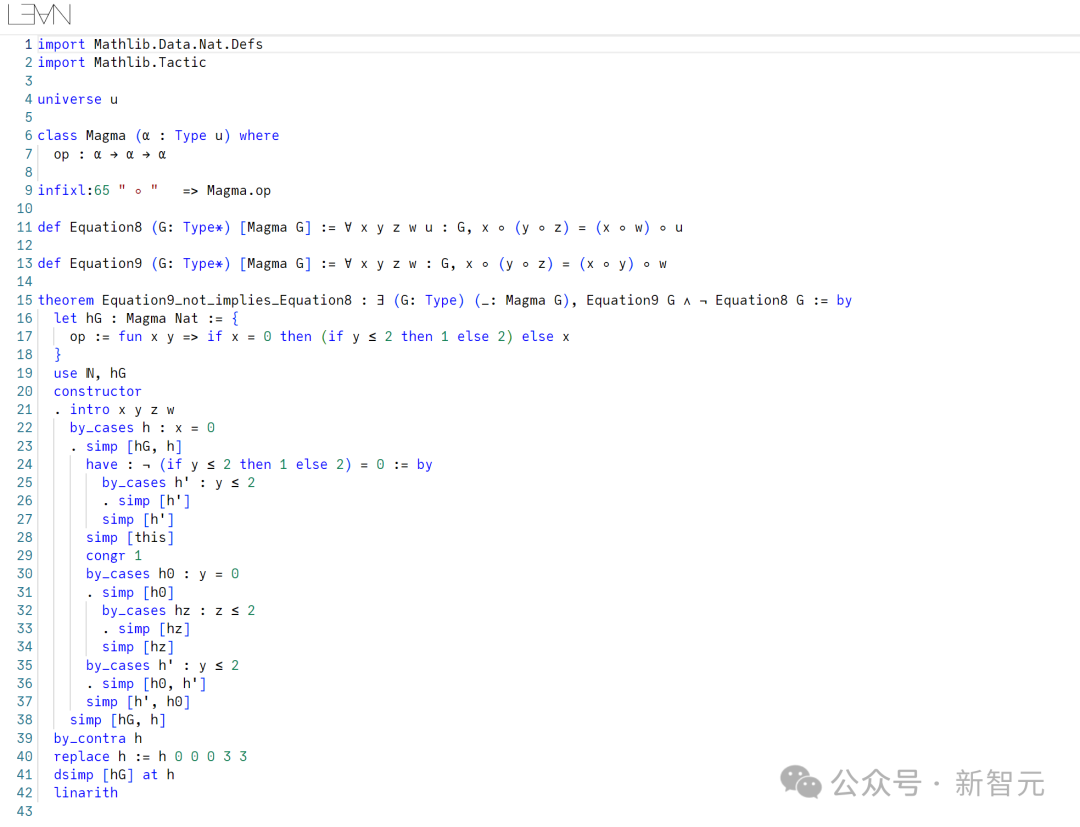
这一结果特别回答了数学问答网站MathOverflow上的一个问题:是否存在介于常数公理(等式1)和结合律公理(等式10)之间的等式公理(equational axioms)。 值得注意的是,这里大多数的蕴含关系都很容易证明。然而,其中存在一个非平凡的蕴含关系。 这个关系是在一个与前述问题密切相关的MathOverflow帖子回答中得到的:


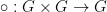 的集合G。
的集合G。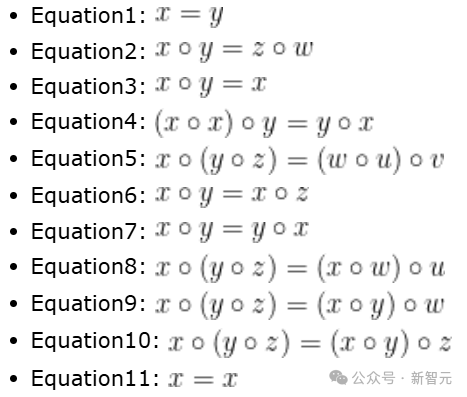

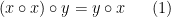
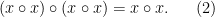
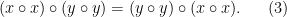




内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢