
Stanford CS224W: Machine Learning with Graphs
By Yuke Wu, Yiwen Zhang and Daniel Zhou for CS 224W course project Fall 2024.
动机
颗粒流(Granular flows)在自然环境和人工环境中无处不在,包括大量离散颗粒(如沙子、砾石或雪)的运动。准确模拟这些流动的能力对于理解和缓解各种岩土灾害(如山体滑坡、泥石流和雪崩)至关重要。

然而,由于包括颗粒相互作用、摩擦以及颗粒材料的复杂行为在内的众多因素的错综复杂的相互作用,颗粒流的数值模拟面临着巨大的挑战。
目前,用于模拟颗粒流的传统数值方法,例如离散元法(Discrete Element Method,DEM) 和物质点法(Material Point Method,MPM),虽然可以提供有价值的见解,但计算成本可能很高,尤其是在处理大型系统或长时间模拟时。DEM 跟踪单个粒子的运动和相互作用,提供高保真结果,但通常需要大量计算资源。另一方面,MPM 将材料离散化为物质点的集合,提供了一种更有效的方法,但可能会牺牲捕捉单个粒子详细行为的准确性。
该领域的持续研究对于开发更高效、更准确、更强大的模拟工具至关重要,最终将在工程、环境管理和灾害防备方面带来更安全、更可持续的实践。
在这篇博文中,我们希望利用机器学习框架基于图神经网络的模拟器 (Graph Neural Network-based Simulators,GNS) 作为替代模型来预测颗粒和流体流动动力学。
图神经网络 (Graph Neural Network,GNN) 的计算效率和通用性使其成为评估流出危险和其他需要大量模拟的颗粒流场景的有前途的工具。具体来说,我们希望展示 GNN 复制颗粒柱或水滴的坍塌及其与障碍物相互作用的能力。
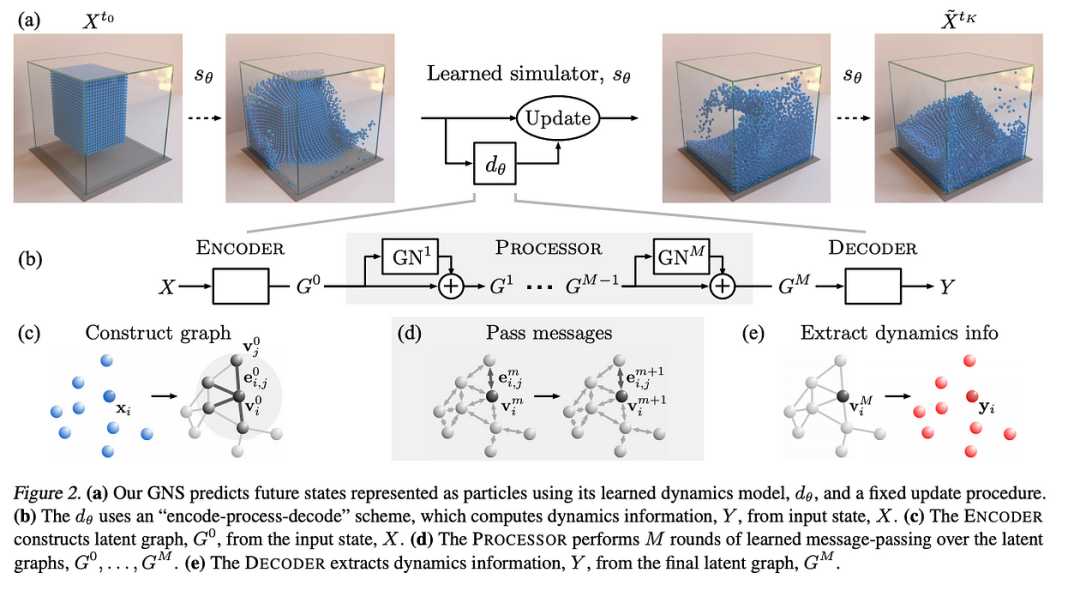
Sanchez-Gonzalez 等人在《Learning to Simulate Complex Physics with Graph Networks》中介绍的 GNS 结构
GitHub 存储库
这是我们的 GitHub 存储库的链接,其中包含我们 GNS 模型的所有代码。README 文件提供了有关如何根据模拟数据训练 GNS 并呈现结果的说明。请下载代码,您应该能够在 VSCode 的帮助下执行训练过程。
基于图形神经网络的模拟器的 Git 存储库。
https://github.com/LeonardZ0731/gns_attention
Colab
这是我们关联的 Google Colab 笔记本的链接。它基于我们的 GitHub 存储库,包含加载数据和执行训练的必要步骤。
https://colab.research.google.com/drive/1G2uEStj3of6zDIGacf03OnEM2usj4crV?usp=sharing&source=post_page-----08ed0a20b28d--------------------------------
任务
在本研究中,我们希望利用所选的 GNS 模型在灵活的基于图的框架中捕捉离散粒子之间的相互作用。MPM 和 SPH 等传统方法模拟基于粒子的相互作用,但对于大规模模拟而言,计算成本很高。GNS 通过使用图传递消息来解决这一挑战,从而能够高效地学习不同条件下的粒子相互作用。
即使设置相同,聚合函数的选择也会产生很大的不同。另外,在这种情况下,Graph Transformer 会有帮助吗?
考虑到这两个问题,我们计划探索从邻近粒子中聚合信息的不同方法,以及这些选择如何影响不同颗粒流的模型准确性。在默认的 GNS 求和聚合器的基础上,我们试图评估最大聚合器、平均聚合器和图Transformer的影响。
最大聚合器突出了粒子邻居的关键特征,这不会稀释强信号,并可能产生更好的模型性能。平均聚合器平滑了连接良好的粒子的影响,提供了稳定性,并避免了求和聚合器可能遇到的对邻域大小的敏感性。图Transformer利用注意力机制,可以区分不同类型的粒子相互作用,这在粒子关系可能因当地条件而异的颗粒流中至关重要。通过允许模型关注相关的邻居,注意力机制可以提高预测准确性,尤其是在粒子相互作用变化很大的情况下。
数据集和预处理
数据集
我们计划为该项目使用两个训练数据集:
一个数据集基于具有单一材料属性的粒状柱塌陷,复制了受控二维环境中的粒状流行为。该数据集包括 26 条方形粒状团块在盒子边界内的粒状流轨迹。该数据集的模拟是使用通过 CB-Geo MPM 代码实现的显式时间积分材料点法进行的。每条轨迹在初始配置、团块大小、位置和速度方面都不同,从而产生了多种粒状塌陷场景。该数据集由 Vantassel 等人 (2022) 推出,可在自然灾害研究数据存储库DesignSafe(https://www.designsafe-ci.org/data/browser/public/designsafe.storage.published/PRJ-3702)上公开获取。
此外,我们还开发了验证数据集来评估模型过度拟合的可能性。这些数据集包含七条矩形颗粒轨迹,每条轨迹都有不同的初始配置,这些配置被有意排除在训练数据集之外。
考虑到我们有限的计算资源,我们还使用了另一个更简单的数据集 WaterDrop。该数据集基于水滴的轨迹。WaterDrop(https://sites.google.com/view/learning-to-simulate/home#h.p_XnIe-peLuIUf) 数据集包含 2k 个粒子,并模拟了 1000 步。

论文中介绍的WaterDrop数据集
预处理
为了正确处理数据,我们首先使用数据增强来增强模型对误差累积的鲁棒性,以便我们的预测结果更加可靠。我们将高斯噪声纳入训练轨迹中的物质点位置。此噪声模拟了在多个模拟时间步中发生的预测误差,其中每个时间步的预测位置均基于前一个预测。
import torch
def get_random_walk_noise_for_position_sequence(
position_sequence: torch.tensor,
noise_std_last_step):
velocity_sequence = time_diff(position_sequence)
num_velocities = velocity_sequence.shape[1]
velocity_sequence_noise = torch.randn(
list(velocity_sequence.shape)) * (noise_std_last_step/num_velocities**0.5)
# Apply the random walk.
velocity_sequence_noise = torch.cumsum(velocity_sequence_noise, dim=1)
return torch.cat([
torch.zeros_like(velocity_sequence_noise[:, 0:1]),
torch.cumsum(velocity_sequence_noise, dim=1)], dim=1)然后,我们将原始材料点数据及其相互作用关系信息编码为顶点和边特征向量以构建图。表示颗粒流的图由一组表示土壤颗粒或颗粒聚集体的顶点组成,而顶点之间的边表示颗粒之间的相互作用。每个顶点将用其当前材料点位置、材料点速度上下文、边界信息、材料点类型嵌入以及表示相应材料点材料属性的可选特征进行编码。数据加载器中使用的 collate 函数应如下所示:
material_property_list = []
for ((particles_positions, particles_type, material_property, particles_count), label) in data:
particles_positions_list.append(particles_positions)
particles_type_list.append(particles_type)
particles_count_list.append(particles_count)
material_property_list.append(material_property)
label_list.append(label)
return ((torch.tensor(np.vstack(particles_positions_list)).to(torch.float32).contiguous(),
torch.tensor(np.concatenate(particles_type_list)).contiguous(),torch.tensor(np.concatenate(material_property_list)).to(torch.float32).contiguous(), torch.tensor(particles_count_list).contiguous(),), torch.tensor(np.vstack(label_list)).to(torch.float32).contiguous())
该图应正确捕捉物质点之间的关系,并作为图神经网络的正确输入。然后,GNN 将在图上执行消息传递。在此过程中,代表物质点的节点将与其相邻节点交换信息。这有助于 GNN 基于这些局部相互作用学习颗粒流的动态。最后,解码器将从最终更新的图中提取物质点的动态。提取的速度、加速度和位置等数据将用于预测颗粒流的未来状态。
基于图神经网络的模拟器
我们将扩展Sanchez-Gonzalez 等人 (2020)(https://arxiv.org/pdf/2002.09405)和Choi 等人 (2023)(https://www.designsafe-ci.org/data/browser/public/designsafe.storage.published/PRJ-3901)提出的图网络模拟器 (GNS) 框架。为了模拟颗粒流的动力学,传统的数值方法(例如材料点法 (MPM) 和光滑粒子流体动力学 (SPH))将颗粒流表示为离散的、相互作用的粒子的集合。这些粒子可以建模为图中的顶点,其相关特征向量编码位置、速度和加速度等属性。顶点之间的有向边可以根据接近度定义,从而以图结构自然编码的方式捕获粒子之间的相互作用。这种基于图的表示保留了问题的置换不变性,同时有效地捕捉了系统的动态行为。GNS 框架通过沿边传递的消息在顶点之间传播信息来处理这些图,以预测后续的粒子运动。
GNS 模型由三个组件组成:编码器、处理器和解码器。
编码器:编码器接收一个输入图 𝐺 = (𝑉, 𝐸),其中 𝑉 为顶点,𝐸 为边,并将其转换为潜在图表示 𝐺_0 = (𝑉_0, 𝐸_0)。此转换使用多层感知器 (MLP) 执行,该感知器嵌入了顶点特征和粒子之间的成对交互。MLP 的构建方式如下:
def build_mlp(
input_size: int,
hidden_layer_sizes: List[int],
output_size: int = None,
output_activation: nn.Module = nn.Identity,
activation: nn.Module = nn.ReLU) -> nn.Module:
layer_sizes = [input_size] + hidden_layer_sizes
if output_size:
layer_sizes.append(output_size)
nlayers = len(layer_sizes) - 1
act = [activation for i in range(nlayers)]
act[-1] = output_activation
mlp = nn.Sequential()
for i in range(nlayers):
mlp.add_module("NN-" + str(i), nn.Linear(layer_sizes[i],
layer_sizes[i + 1]))
mlp.add_module("Act-" + str(i), act[i]())
return mlp在我们当前的实现中,我们有 30 个用于 2D 颗粒塌陷训练的节点特征,其中包括 5 个速度时间步长以提供足够的速度背景(5*2 = 10 个特征)、4 个用于节点与边界之间距离的特征以预测边界产生的摩擦,以及 16 个用于不同粒子类型的不同嵌入的特征以区分不同的材料特性。对于边,我们仅在两个节点在 0.03 m 的连接半径内时才在它们之间构建边。我们有 3 个边特征,其中包含 2 个用于两个节点在 x 和 y 方向上的位移的特征和 1 个用于两个节点之间距离的特征。为了嵌入节点,我们使用一个具有 30 个输入维度、128 个隐藏维度和 128 个输出维度的两层 MLP。同样,为了嵌入边,我们使用一个具有 3 个输入维度、128 个隐藏维度和 128 个输出维度的两层 MLP。
处理器:编码器将节点和边嵌入到具有 128 维嵌入的潜在图中后,处理器随后在潜在图上应用消息传递方案进行 𝑀 次迭代,其中 𝑀 是控制传播步骤数的超参数。每次消息传递迭代都会根据邻居的信息更新顶点的特征向量,从而使网络能够对多个步骤中的局部交互进行建模。在我们当前的实现中,我们选择 M 为 10,这意味着我们有 10 个 MLP 堆栈来处理动态信息。我们将求和实现为基准的聚合函数。
class InteractionNetwork_add(MessagePassing):
def __init__(
self,
nnode_in: int,
nnode_out: int,
nedge_in: int,
nedge_out: int,
nmlp_layers: int,
mlp_hidden_dim: int,
):
super(InteractionNetwork, self).__init__(aggr='add')
self.node_fn = nn.Sequential(*[build_mlp(nnode_in + nedge_out,
[mlp_hidden_dim
for _ in range(nmlp_layers)],
nnode_out),
nn.LayerNorm(nnode_out)])
self.edge_fn = nn.Sequential(*[build_mlp(nnode_in + nnode_in + nedge_in,
[mlp_hidden_dim
for _ in range(nmlp_layers)],
nedge_out),
nn.LayerNorm(nedge_out)])
def forward(self,
x: torch.tensor,
edge_index: torch.tensor,
edge_features: torch.tensor):
x_residual = x
edge_features_residual = edge_features
x, edge_features = self.propagate(
edge_index=edge_index, x=x, edge_features=edge_features)
return x + x_residual, edge_features + edge_features_residual
def message(self,
x_i: torch.tensor,
x_j: torch.tensor,
edge_features: torch.tensor) -> torch.tensor:
edge_features = torch.cat([x_i, x_j, edge_features], dim=-1)
edge_features = self.edge_fn(edge_features)
return edge_features
def update(self,
x_updated: torch.tensor,
x: torch.tensor,
edge_features: torch.tensor):
x_updated = torch.cat([x_updated, x], dim=-1)
x_updated = self.node_fn(x_updated)
return x_updated, edge_features在此基础上,我们将均值、最大值和多头注意力实现为不同的聚合。在本报告中,我们计划探索不同聚合函数的性能。均值和最大值聚合函数的实现与求和非常相似。然而,多头注意力则截然不同。
主要思想是计算节点和边的查询、键和值向量,然后使用这些向量生成注意权重来更新节点和边的嵌入。我们在这里采用了多头机制,将特征嵌入维度划分为 H 个头。因此每个头都包含一段特征嵌入。
边的注意力分数是根据其自身的边特征(边-边分数)、接收者节点特征(边-接收者分数)和发送者节点特征(边-发送者分数)计算的。
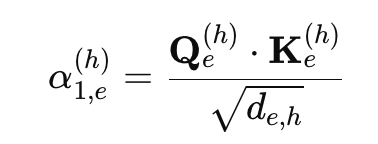
其中alpha_{1, e}^{(h)}是边到边注意力分数,Q_e^{(h)}是边的一个头查询,K_e^{(h)}是边的一个头键,d_{e,h}是头特征的长度。
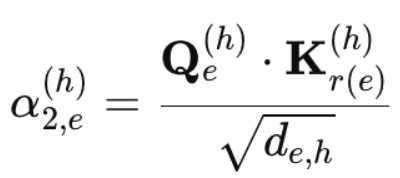
其中,类似地,alpha_{2, e}^{(h)}是边缘接收器注意力分数,并且K_{r(e)}^{(h)}是接收器的一个头键。
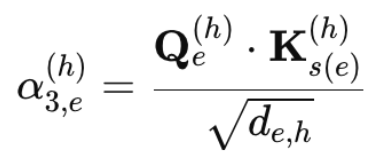
其中类似地alpha_{3, e}^{(h)}是边缘发送者注意力分数并且K_{s(e)}^{(h)}是发送者的一个头键。
计算这些分数后,我们将它们堆叠起来,并在三个通道上应用 softmax 来规范化注意力权重。使用这些注意力权重,我们聚合值向量,为每个 head 生成一个新的边缘特征。最后,我们将所有 head 连接起来,并通过 MLP 进行馈送,以生成更新的边嵌入。
类似地,节点的注意力分数是根据其他节点(节点-节点分数)和传入边(节点-边分数)计算得出的。
节点间得分计算方法为
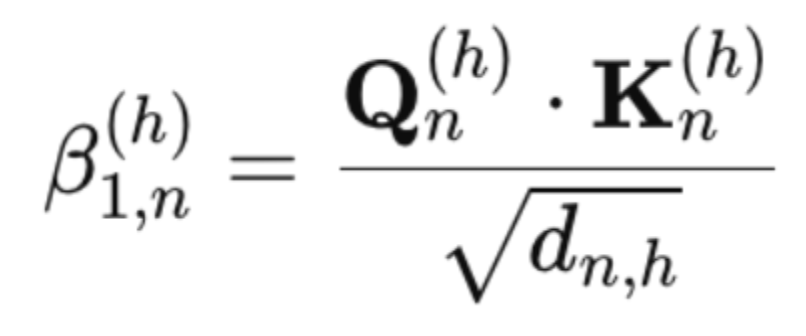
其中,Q_n^{(h)}是每头节点数的查询,K_n^{(h)}是每头节点数的关键,d_{n,h}是一个头特征的长度。
类似地,节点边得分通过以下公式计算:
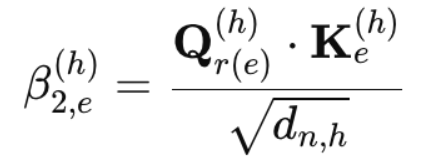
其中,Q_r^{(e)}是接收方的一个头查询,K_e^{(h)}是每个头的边的关键。
与边注意力分数类似,我们也对这些分数进行归一化,并聚合值向量,为每个 head 生成一个新的节点特征。将所有 head 连接起来并输入到 MLP 后,就会生成一个新的节点嵌入。
我们目前利用 PyG 的消息传递类,其公式如下:
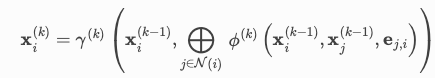
其中gamma^{(k)}是一个 2 层 MLP,具有 128 * 2 个输入维度,以及 128 个潜在维度和输出维度,用于更新每个节点嵌入,并且phi^{(k)}是一个 2 层 MLP,具有 128 * 3 个输入维度,以及 128 个潜在维度和输出维度,用于输出来自前一层的消息。
解码器:最后,解码器从处理器获取更新后的潜在图并提取动态量,例如加速度。为了实现这一点,我们再次使用了两层 MLP,其输入、潜在和输出维度均等于 128。在学习后的 MLP 解码器提取加速度后,可以通过有限差分法计算粒子速度和位移,为模拟中的下一个时间步提供更新。
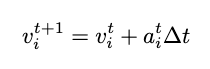
其中v_i^{t+1}是粒子i在t + 1时间帧的速度,a_i^{t}是粒子i在时间帧t预测的加速度, delta t 是数据集每帧的时间步长。同样,位移的更新是
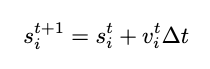
其中s_i^{t+1}是粒子i在时间帧t + 1处的位移。我们的解码器实现是:
class Decoder(nn.Module):
def __init__(
self,
nnode_in: int,
nnode_out: int,
nmlp_layers: int,
mlp_hidden_dim: int):
"""
Args:
nnode_in: Number of node inputs.
nnode_out: Number of node outputs.
nmlp_layer: Number of hidden layers in the MLP.
mlp_hidden_dim: Size of the hidden layer.
Latent dimension is of size 128.
"""
super(Decoder, self).__init__()
self.node_fn = build_mlp(
nnode_in, [mlp_hidden_dim for _ in range(nmlp_layers)], nnode_out)
def forward(self,
x: torch.tensor):
return self.node_fn(x)结果
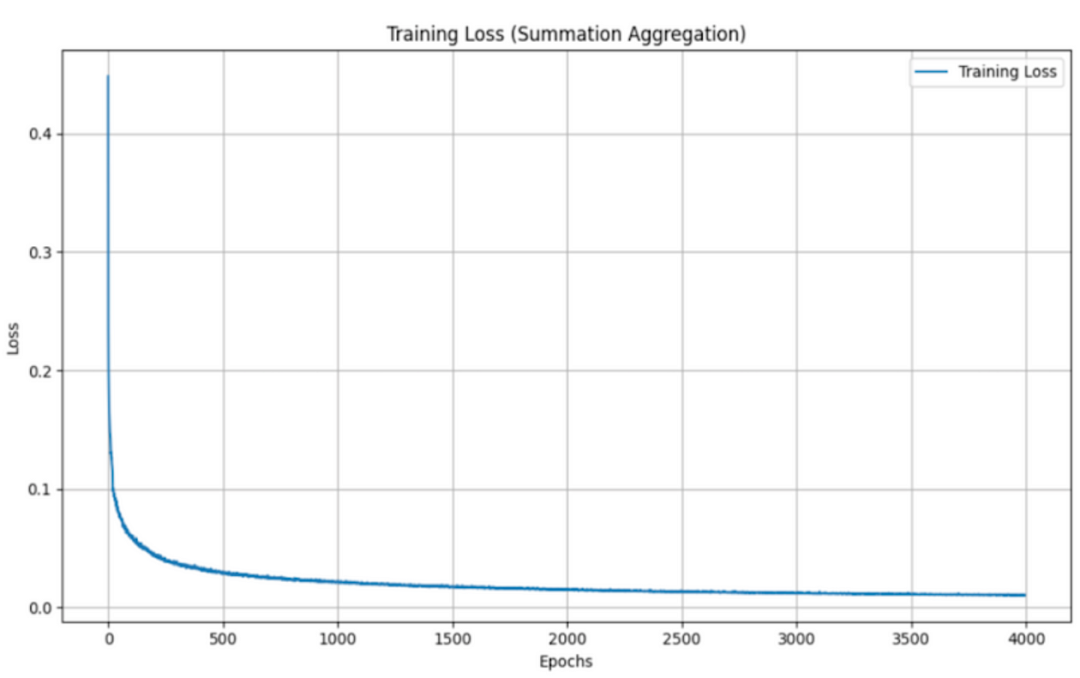
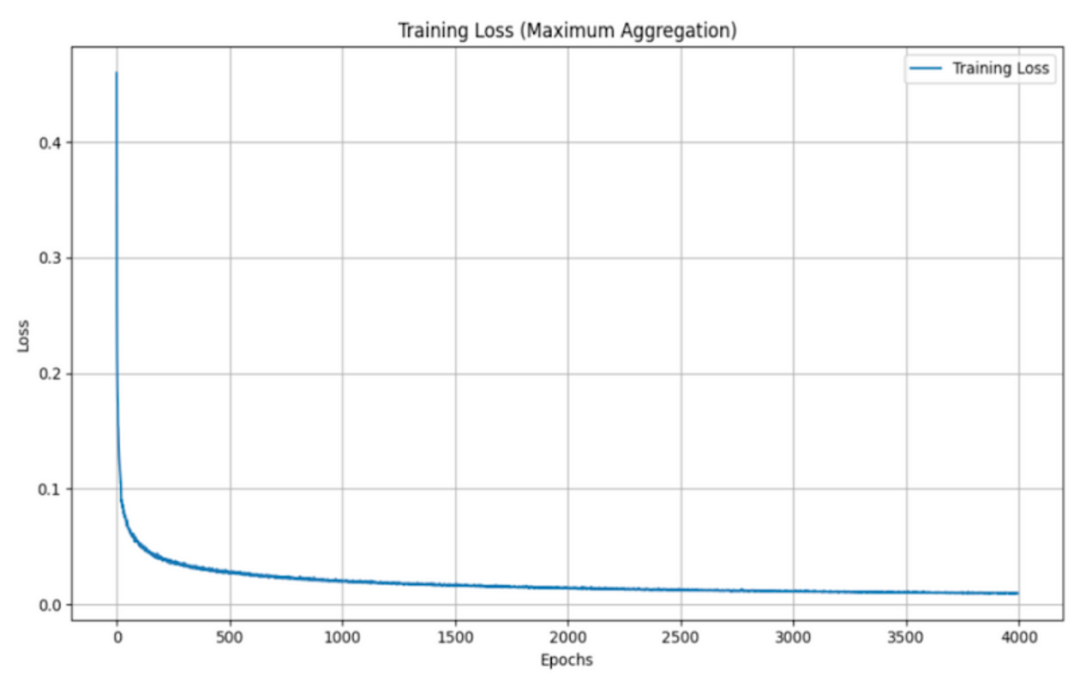
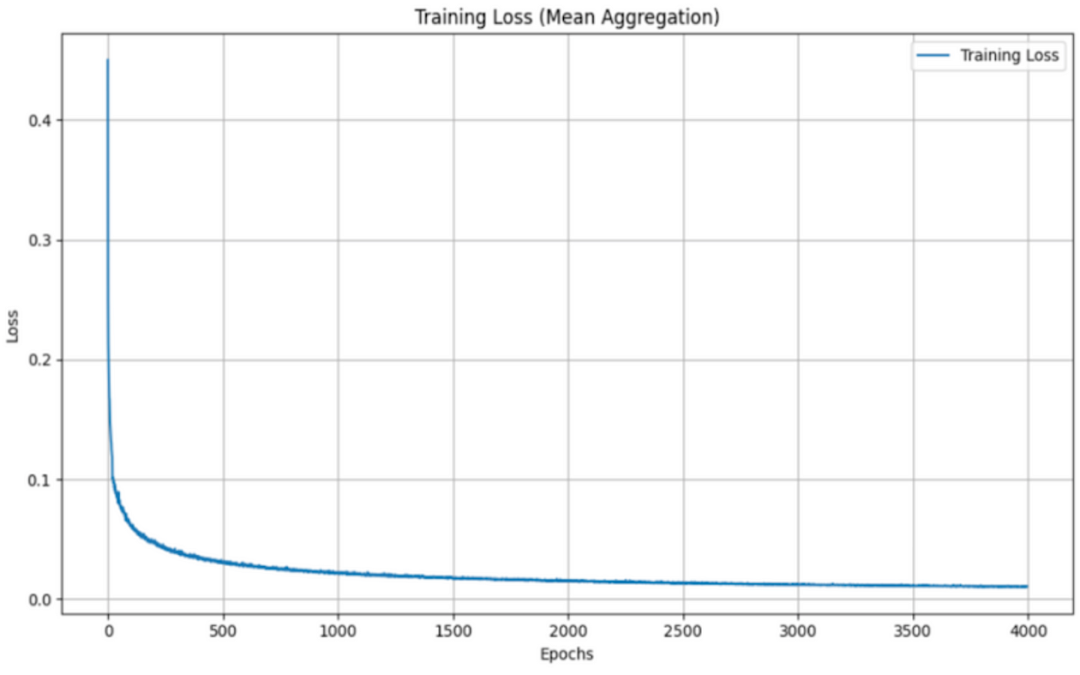
当使用不同的聚合函数(平均值、最大值、总和和 Graph Transformer)评估 GNS 模型的训练损失时,会发现训练损失呈现出一致的模式,且各个函数之间的变化最小。
汇总聚合:
最大聚合:
均值聚合:
Graph Transformer:
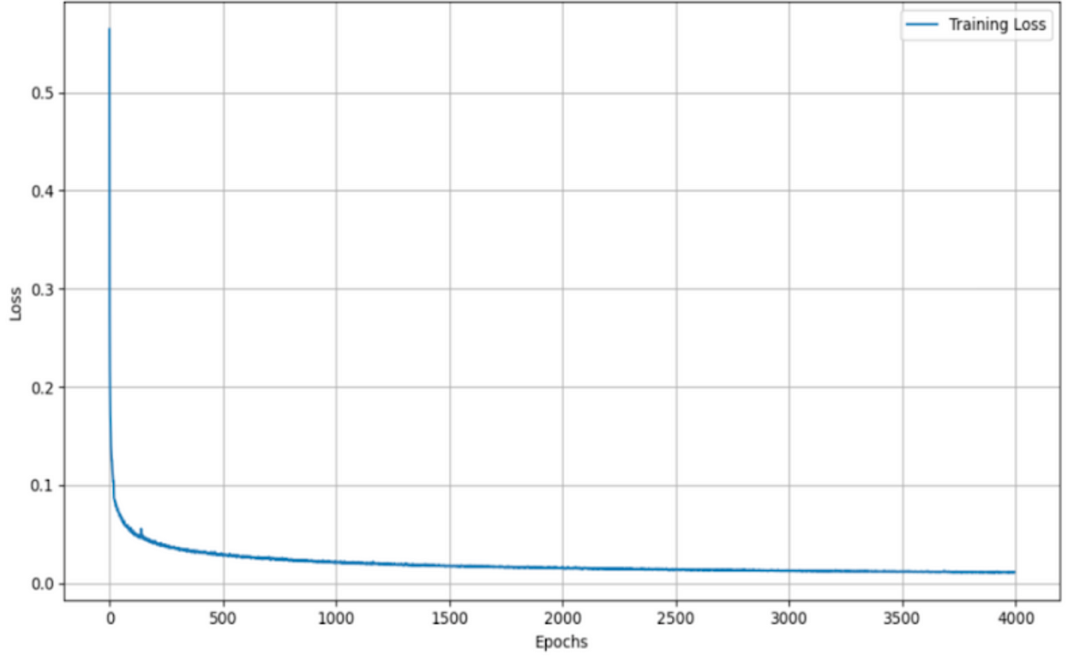
尽管这些函数在结合邻居信息的方式上有所不同(平均贡献、最大强调最主要信号、汇总总贡献和结合基于注意的加权的 Graph Transformer),但训练损失的相似性表明,该模型的学习和泛化能力对于聚合方法的选择相对稳健。这一观察结果凸显了 GNS 模型的多功能性,并表明聚合函数的选择可能更多地取决于计算效率或可解释性,而不是训练期间的性能差异。
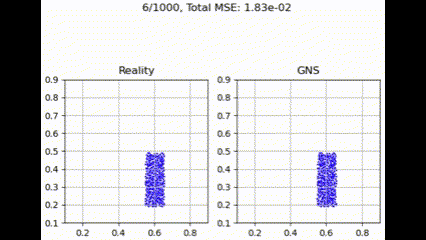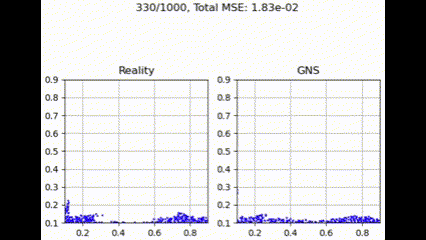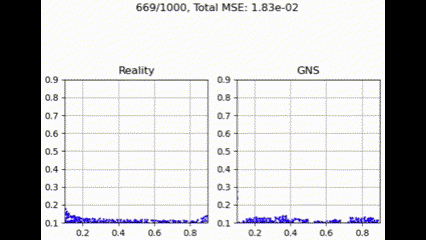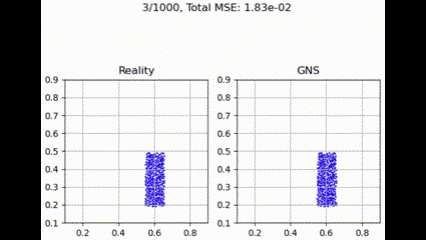
在测试集上进行评估时,GNS 模型在不同聚合函数下表现出细微差异。如下面的示例所示,聚合函数通常呈现出性能层次,其中 max 实现最低损失,其次是 summation、Graph Transformer 和 mean。
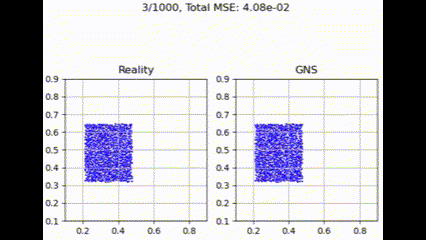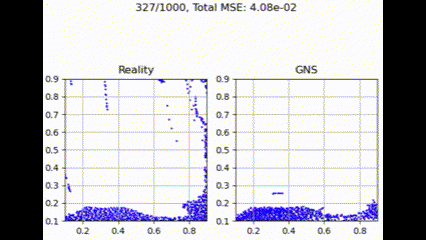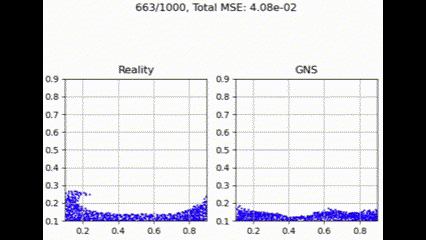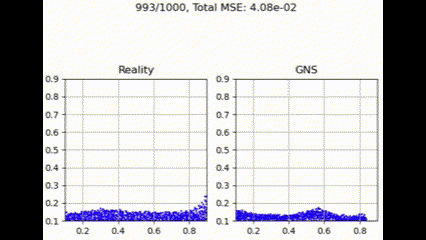
汇总聚合
均值聚合
最大聚合
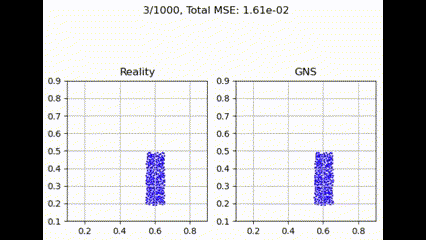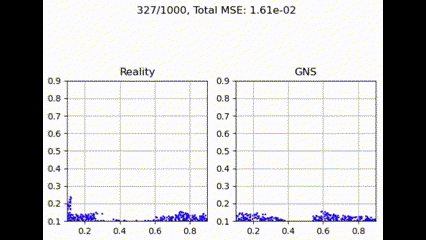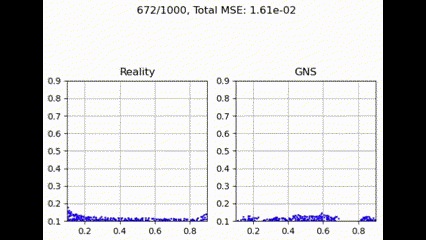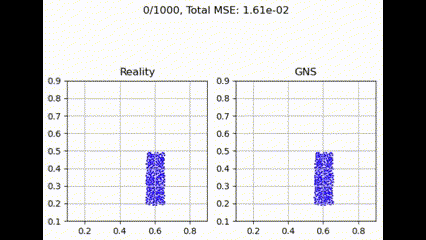
Graph Transformer
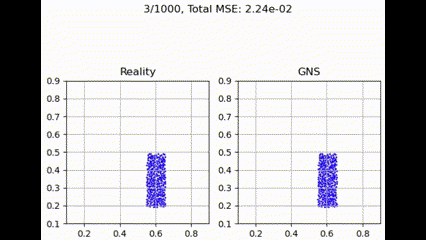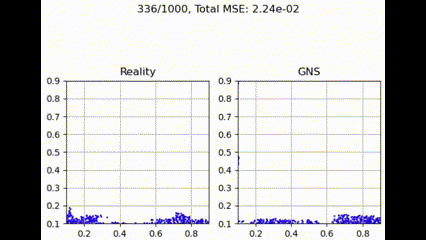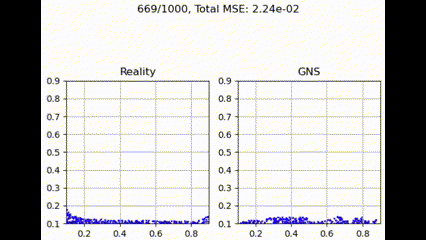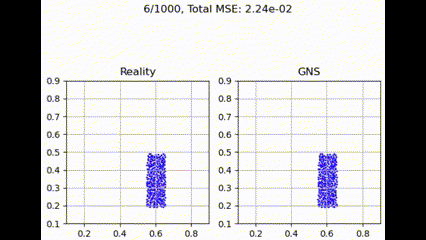
最大聚合函数在捕获和利用图结构中所有邻居贡献方面更为有效。这提供了最佳性能,可能是因为它强调了最强的邻居贡献,可能有利于主要特征更具信息量的粒度流模拟任务。
求和函数保留了信号的总幅度,其性能表现中等。尽管求和聚合通常被认为是最具表现力的,但我们认为,它在图结构中充分利用邻居贡献的能力在粒状流模拟任务中并不那么重要。这可能是因为它更善于保留信号的总幅度,这使得它在特征的累积效应至关重要的任务中更有用。
Graph Transformer 具有注意力机制,可提供更细致的权重,但由于其依赖于学习到的注意力分数,因此可能表现不佳,这可能会增加训练过程中的复杂性和潜在的不稳定性。不过,使用更大的训练数据集或更多的训练迭代,性能可能会有所提高。
平均函数(即对邻近贡献进行平均)似乎会稀释单个信号的重要性,从而导致相对较高的损失。
我们认为最大值是水滴任务中最好的聚合函数,因为考虑最强邻域贡献的能力在特定流动的建模中起着更关键的作用。这一特性似乎对需要全面表示底层动态的任务特别有利,例如模拟水滴等颗粒流动。
结论
总之,本研究证明了图网络模拟器 (GNS) 作为模拟粒状流动力学的替代模型的有效性,为 MPM 和 SPH 等传统数值方法提供了一种计算效率高的替代方案。通过采用各种聚合函数(求和、平均值、最大值和图Transformer),我们探索了它们对模型性能和训练效率的影响。我们的结果表明,虽然不同聚合方法之间的训练损失差异很小,但聚合的选择会显著影响测试性能。最大聚合函数是最有效的,它捕获了对准确建模粒状流至关重要的主导邻居贡献。这凸显了选择适合特定任务(例如粒状流模拟)动态的聚合策略的重要性。
总体而言,GNS 模型的稳健性和多功能性凸显了其作为评估复杂颗粒流的宝贵工具的潜力,对推进更安全、更高效的工程和环境管理实践具有重要意义。未来的工作可能包括将这些发现扩展到更大的数据集、探索其他图架构以及评估该模型对三维流动场景的适应性。



内容中包含的图片若涉及版权问题,请及时与我们联系删除




评论
沙发等你来抢