摘要


自组织临界性的概念，例如沙堆模型，能否在连续相变的框架内加以描述？在本文中，我们提供了大量数值证据支持肯定的答案。具体而言，我们将Bak，Tang和Wiesenfeld（BTW）以及Manna沙堆模型作为从无序到有序相的渗流转变的实例进行探讨。为了便于分析，我们引入了掉落密度（drop density）的概念——一个可连续调节的控制变量，用于量化添加到一个位置的颗粒的平均数量。通过调整这个变量，我们观察到沙堆从亚临界相到临界相的变化。此外，我们将从沙堆开始时发生的最大雪崩的缩放大小定义为自组织临界转变的序参量，并分析其缩放行为。另外，我们计算了相关长度指数，并注意到其在临界点附近发散。对于 BTW 沙堆的临界点，雪崩大小分布的有限尺寸缩放分析效果很好。


研究领域：自组织临界性，沙堆模型，临界相变，BTW模型、Manna模型

 

论文题目：Describing self-organized criticality as a continuous phase transition
发表时间：2025年2月12日
论文地址：https://journals.aps.org/pre/abstract/10.1103/PhysRevE.111.024111
期刊名称：Physical Review E




当沙堆遇见相变




1987年，Bak、Tang和Wiesenfeld提出自组织临界性（SOC）概念，认为沙堆模型等系统无需精细调控参数即可自发形成长程关联的临界状态，这一理论的提出解释了地震、森林火灾等现象的幂律分布特征。然而，SOC与传统连续相变（如铁磁相变）的关系成谜——前者“无参数调节”的特性似乎与后者对临界点的严格依赖背道而驰。最新发表在Physical Review E的一篇突破性研究，通过巧妙的变量定义与数值实验，首次将SOC严格纳入连续相变的理论框架。

详情可查看自组织临界的百科词条：https://wiki.swarma.org/index.php/%E8%87%AA%E7%BB%84%E7%BB%87%E4%B8%B4%E7%95%8C%E6%80%A7





从“自组织”到“可控相变”




研究者选取经典的BTW沙堆模型（确定性规则）和Manna沙堆模型（随机规则）作为突破口。传统SOC认为系统通过动力学过程自然进入临界态，但论文提出了逆向思维——外部驱动中的随机扰动或许隐含着一个连续可调的“控制变量”。研究者引入了一个新物理量掉落密度（drop density，τ），定义为单位时间内每个格点平均接收的沙粒数，临界性参数τc定义为系统进入稳态时的τ值。通过精确调控τ，沙堆系统展现了清晰的临界相变特征：

  • 亚临界相（τ<τc）：雪崩以短程、小尺度为主；

  • 临界相（τ≈τc）：雪崩覆盖全系统尺度；

  • 超临界相（τ>τc）：长程关联主导，系统进入自持临界态。




雪崩尺寸：SOC相变的“序参量”




传统相变中，序参量（order parameter）是相态的标志，例如铁磁相变中的磁化强度。在这里，研究者创新地将“最大雪崩尺寸”映射为SOC的序参量，对不同模型需要进行归一化处理。在BTW模型中，该序参量定义为最大雪崩总崩塌次数相对系统体积的比值；而Manna模型则采用最大雪崩覆盖面积占比用于度量“最大雪崩尺寸”。

数值模拟结果显示，当τ接近临界值 τc 时，该序参量发生剧烈的跃迁，其标度指数（β≈0.132-0.193）与二维渗流理论高度吻合；研究者还发现，雪崩尺寸分布的有限尺寸标度分析在临界点完美坍塌，验证了系统的普适性特征。




“掉落密度”如何关联临界性？




驱动SOC的掉落密度背后是深层的相变动力学：

关联长度发散：通过测量临界性参数τc(L) 随系统尺寸L的演化，发现关联长度指数ν≈0.8-0.9，与二维普通渗流中的参数ν≈1.3形成比较；

守恒量：在临界点，系统净流出量趋近于零，证实τc与平均沙粒高度高度关联。

动力学路径统一：无论是确定性（BTW）还是随机性（Manna）规则，两者在临界指数上仅有细微差异，揭示了SOC鲁棒性与微观规则机制的深层联系。




启示：自组织临界性的统一图景




这项研究将SOC重新定位为“参数隐含的可调相变”：外部驱动中的随机扰动虽看似无序，实则通过动力学反馈形成等效控制变量。这颠覆了“SOC无需参数调控”的传统认知，为地震预测、电网崩溃等真实临界现象提供了新的建模工具。

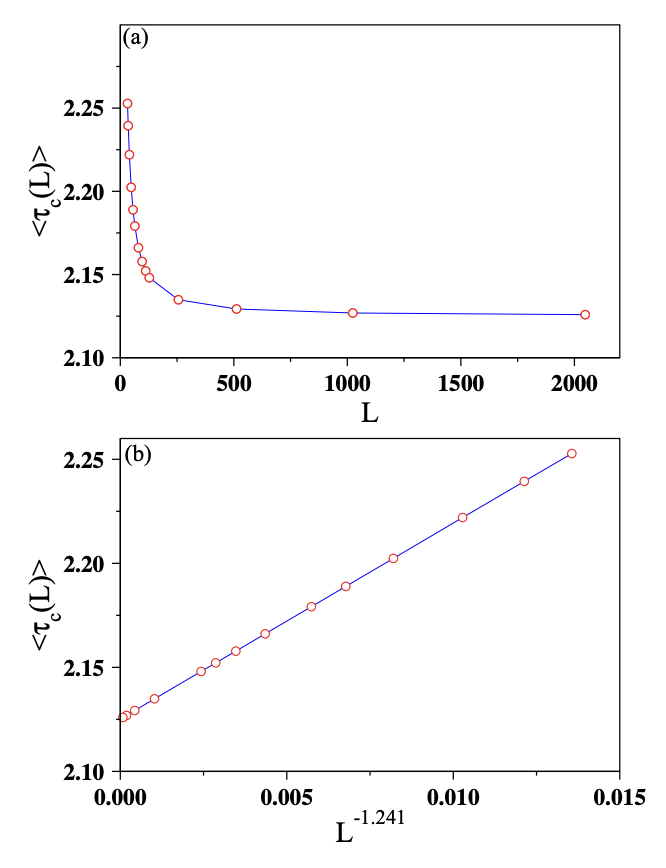
图 1. BTW模型：(a)用首次跨越型雪崩(spanning avalanche)估计的临界掉落密度的平均值与系统大小L作比较。(b)用临界掉落密度的平均值与L-1.141作了对比，得到了最佳拟合直线临界掉落密度的平均值 = 2.1252 + 9.396.L-1.141，τc = 2.1252和1/ν = 1.241。


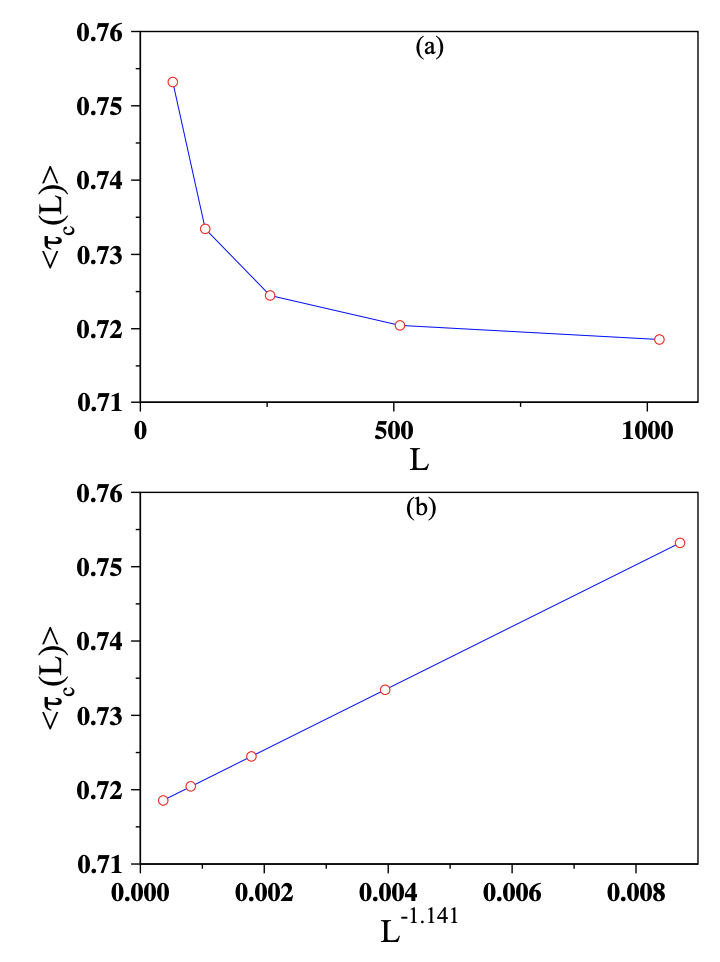
图 2. Manna模型：(a)利用跨越型雪崩估算了临界掉落密度的平均值。(b) 临界掉落密度的平均值已在L-1.141上绘制，以获得最佳拟合直线，该直线外推τc = 0.7170和1/ν= 1.141。



彭晨 | 编译



复杂网络动力学读书会


集智俱乐部联合合肥工业大学物理系教授李明、同济大学副教授张毅超、北京师范大学特聘副研究员史贵元与在读博士生邱仲普、张章共同发起「复杂网络动力学」读书会。本次读书会将探讨：同步相变的临界性、如何普适地刻画多稳态与临界点、如何识别并预测临界转变、如何通过局部干预来调控系统保持或回到期望稳态、爆炸逾渗临界行为的关键特征、不同类型的级联过程对逾渗相变的影响有何异同、高阶相互作用的影响能否等效为若干简单机制的叠加、如何有效地促进人类个体间的合作等问题。

读书会计划从3月7日开始，每周五晚19:30-21:30进行，持续8-10周。诚挚邀请领域内研究者、寻求跨领域融合的研究者加入，共同探讨。


图片


详情请见：复杂网络上的自组织与集体行为：从扩散、相变到博弈 | 读书会启动



推荐阅读
1. 复杂网络中的动力学：从理论突破到地球生态的跨学科对话
2. 自组织临界：为什么大规模灾难频繁发生，且难以预测？
3. 《大自然如何运作》：关于自组织临界性的科学｜汤超院士作序推荐
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 解锁集智全站内容，开启新年学习计划

6. 加入集智，一起复杂！



点击“阅读原文”，报名读书会

内容中包含的图片若涉及版权问题，请及时与我们联系删除