CMP | 基于朗之万动力学的量子优化算法

北京大学前沿计算研究中心 2025-02-22 13:00 分享

以下文章来源于mp.weixin.qq.com

关键词：量子优化算法朗之万动力学开放量子系统

导读

本文是发表在 Communications in Mathematical Physics 上的论文 Quantum Langevin Dynamics for Optimization 的详细解读。该项研究由北京大学李彤阳课题组完成。论文第一作者为陈哲睿和陆宇晨，合作者包括王昊、刘逸舟，通讯作者为李彤阳。

论文首次利用了量子朗之万动力学（QLD）来解决优化问题，特别是那些对传统优化算法构成极大困难的非凸目标函数。具体来说，本文考察了一个与无限热浴耦合的动力学系统，系统和热浴之间的相互作用会在系统中引入随机的量子噪声和阻尼效应，从而将系统引导至接近目标函数全局最小值的稳态。本文在理论上证明了 QLD 在凸目标函数场景下的收敛性，表明在低温极限下，系统的平均能量可以以指数收敛速率趋于零。在数值实验中，本文首先通过追溯 QLD 的起源（如自发辐射现象）验证其能量耗散性。此外，本文对各参数的影响进行了详细讨论。最后，通过与经典的 Fokker-Planck-Smoluchowski 方程对比观察到的现象，本文提出了一种时间依赖的 QLD，即将温度和 $\hbar$ 设置为时间依赖参数。理论分析证明，这种时间依赖的 QLD 比时间不变的 QLD 收敛性更优，并且在许多非凸优化问题中，相较于一系列最先进的量子和经典优化算法表现出更优越的性能。

论文链接：

https://link.springer.com/article/10.1007/s00220-025-05234-4

引言

连续优化问题广泛应用于机器学习、物理建模等领域，可以将其形式化为

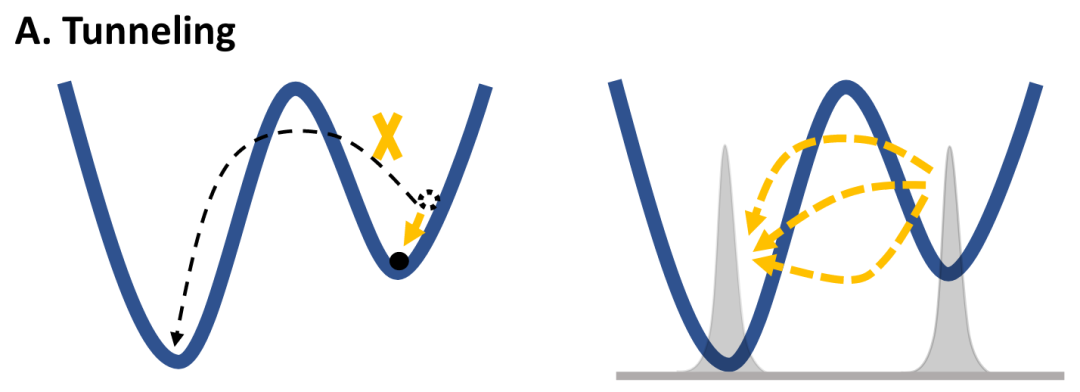
$\min_x V(x)$ 其中 $V(x)$ 为连续的目标函数。在处理非凸目标函数时，如何避免经典算法在搜索全局最优解的过程中无法逃离局部最优解仍然是一个巨大挑战。通常，我们通过在经典算法中添加随机项来解决凸优化问题，即随机梯度下降算法（Stochastic Gradient Descent，SGD）。近年来，随着量子科技的迅猛发展，量子算法逐渐在优化问题中展现出巨大的潜力，例如量子绝热算法（Quantum Annealing Algorithm，QAA）。而基于量子动力学构造的量子算法，例如量子哈密顿梯度下降算法（Quantum Hamiltonian Descent，QHD）^[1]，本身就能够利用量子隧穿的效应来避免陷入局部最优解，如图1所示。

图1. 量子隧穿效应

现有工作已经表明，非凸优化问题中噪声可以提高经典算法的性能，但量子噪声对于量子优化算法的作用尚未充分探索。

于是本文试图将量子噪声的效应引入量子优化算法中研究了量子朗之万动力学（Quantum Langevin Dynamics, QLD）。QLD 是一个基于开放量子系统的 Lindblad 方程的理论框架，广泛用于模拟开放量子系统与环境的相互作用。系统与环境的相互作用表现为系统的噪声和耗散，使得系统拥有一定的逃离局部极小值，并最终收敛至稳态的能力，如图2所示。QLD 结合了朗之万方程和量子力学的特点，通过引入随机噪声和耗散项来描述量子系统在热浴中的动力学行为。

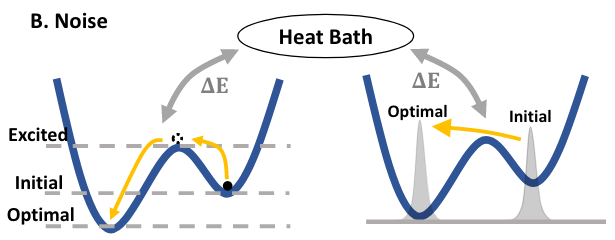
图2. 量子噪声效应

问题设定

考虑由如下朗之万动力学控制的动力学系统

$\mathcal{L}(\rho) = -\frac{i}{\hbar}[H,\rho]+(2L\rho L^\dagger – [L^\dagger L, \rho]_+).$ 其中， $[A,B]=AB-BA$ ， $[A,B]_+ = AB+BA$ ， $H = \frac{p^2}{2m} + V$ 为系统的哈密顿量， $L$ 为 Lindblad 算符。受到阻尼谐振子泛函以及前人工作的启发^[2]，本文将 $L$ 的具体形式取为 $x$ 和 $p$ 的线性叠加，

$L = \mu x + i \nu p, L^\dagger = \mu x-i\nu p$ 其中， $\mu$ 和 $\nu$ 为两个常数与系统质量 $m$ ，约化普朗克常数 $\hbar$ ，以及耗散系数 $\eta$ 相关的常数。该形式使得上述朗之万动力学能够同时适用于高温和低温情况，并且避免了传统的 CL 主方程会出现违背量子态正定性的问题。

将系统的势能 $V$ 设置为待优化的目标函数，本文希望通过调节动力学系统的参数来使得动力学系统演化后达到稳态时，其概率密度分布能够收敛至全局极小值附近。

理论结果

假设目标函数全局极小值位于 $x^*$ 。我们用 $\langle A\rangle_t = Tr[\rho_t A]$ 来表示算符 $A$ 在 $t$ 时刻关于量子态 $\rho_t$ 的平均值。

凸优化问题中的收敛性。当目标函数 $V(x)$ 为凸函数，且 QLD 的参数（阻尼率（ $\eta$ ）、温度（ $T$ ）、普朗克常数（ $\hbar$ ））在演化中保持恒定时，本文证明系统的势能平均值满足

$\langle V\rangle_t - V(x^*) \le (2+O(\hbar \Omega/kT))kT + O(e^{-\eta t})$ 当 $\hbar\Omega/kT \ll 1$ 且 $kT\to 0$ 时，势能函数平均值随时间收敛至全局极小值且收敛速率为 $O(e^{-\eta t})$ （定理 1）。当参数随时间变化时（ $\hbar(t)$ 随时间单调递减， $T(t)$ 需满足引理3中的条件时），本文证明势能平均值仍然收敛，收敛速率为 $O(e^{-\int_0^t \eta(t’) dt’})$ 。

Quasar凸问题^[3]中的收敛性。Quasar 凸函数为非凸函数，但性质与凸函数类似，只有一个全局极小值，且满足 $x\nabla V(x)\ge rV(x)$ ， $r\in (0,1)$ 。本文证明了 QLD 在该情况下，当参数不随时间变化时，势能平均值满足

$\langle V\rangle_t - V(x^*) \le (2+O(\hbar \Omega/kT))kT/r + O(e^{-\eta/r t})$ 当 $\hbar\Omega/kT \ll 1$ 且 $kT\to 0$ 时，势能函数平均值随时间收敛至全局极小值且收敛速率为 $O(e^{-\eta/r t})$ （定理 3）。当参数随时间变化时，本文证明势能平均值仍然收敛，收敛速率为 $O(e^{-\int_0^t \eta(t’)/r dt’})$ 。

二次型问题下的解析解。当势能函数为二次型时， $V(x) = 1/2m\Omega^2 x^2$ ，本文给出了势能函数平均值随时间变化的解析解。令 $\langle H\rangle_t = (n_t +1/ 2)\hbar \Omega$ 。当 QLD 参数不随时间变化时， $\langle H\rangle_t$ 满足

$\frac{d \langle H\rangle_t}{dt} =( -2\eta \langle H\rangle_t - 1 + coth(\frac{\hbar\Omega}{kT}))\eta \hbar \Omega.$ 由此可知， $n_t \to 1 /2 (coth(\frac{\hbar\Omega}{kT})-1)$ ，且当 $T\to 0$ 时，系统最终收敛至基态， $n_t \to 0$ 。

数值实验

针对有解析解的二次型，本文进行了数值实验，证明了理论和数值解上的一致性，如图3所示：可以观察到系统从一个近似均匀分布的初态出发，演化足够长时间之后，能够达到解析解所展示的基态。

图3. QLD 在二次型目标函数下的演化结果

对于含时的 QLD，本文将其与一些优秀的量子和经典优化算法进行了比较，包括 QHD, QAA, SGD, NAGD。各种算法相互比较的指标为算法成功概率，被定义为在局部最小值附近的一个小区间内的概率之和。用于测试性能的目标函数各自有着不同特征，被分成了如表格1所示的如下几类，

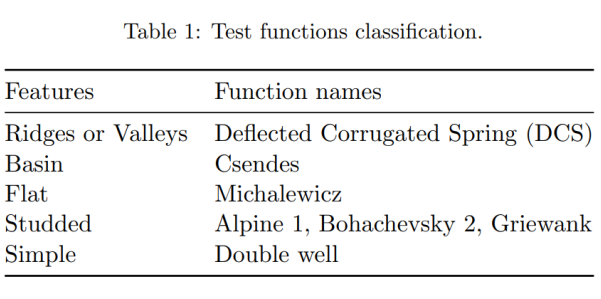
表1. 测试函数

最终得到了以下成功概率随时间的结果，如图4所示：

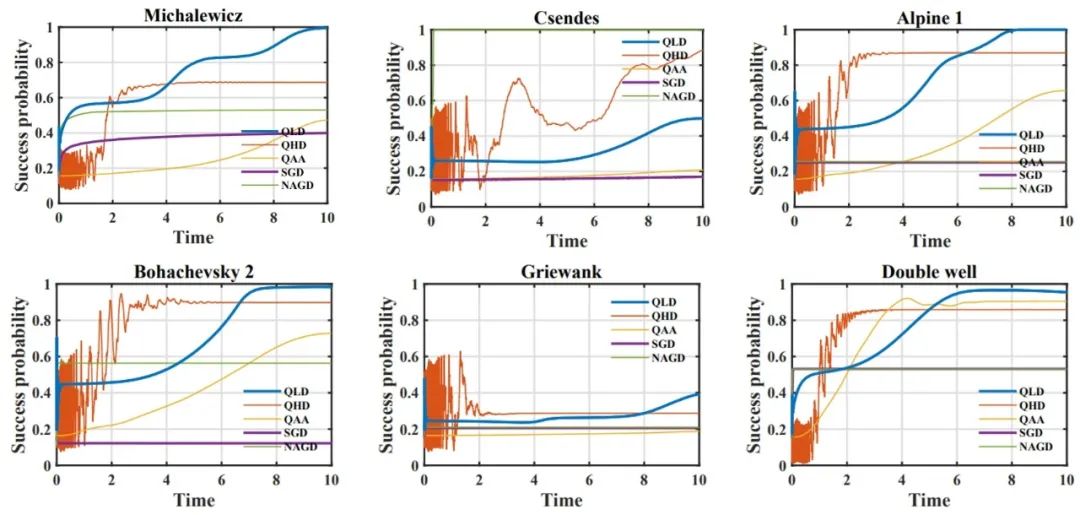
图4. 不同算法在不同测试函数下的成功概率

可以看到在绝大多数目标函数上，QLD 能够获得较好的表现。以 Michalewicz 函数为例，不同算法的收敛过程如图5所示。从图6中可以观察到，QLD 在演化过程的后半段，能够很大概率地收敛到左侧的全局最小值附近，然而其他算法都有一定一部分概率被卡在右侧局部最小值附近。

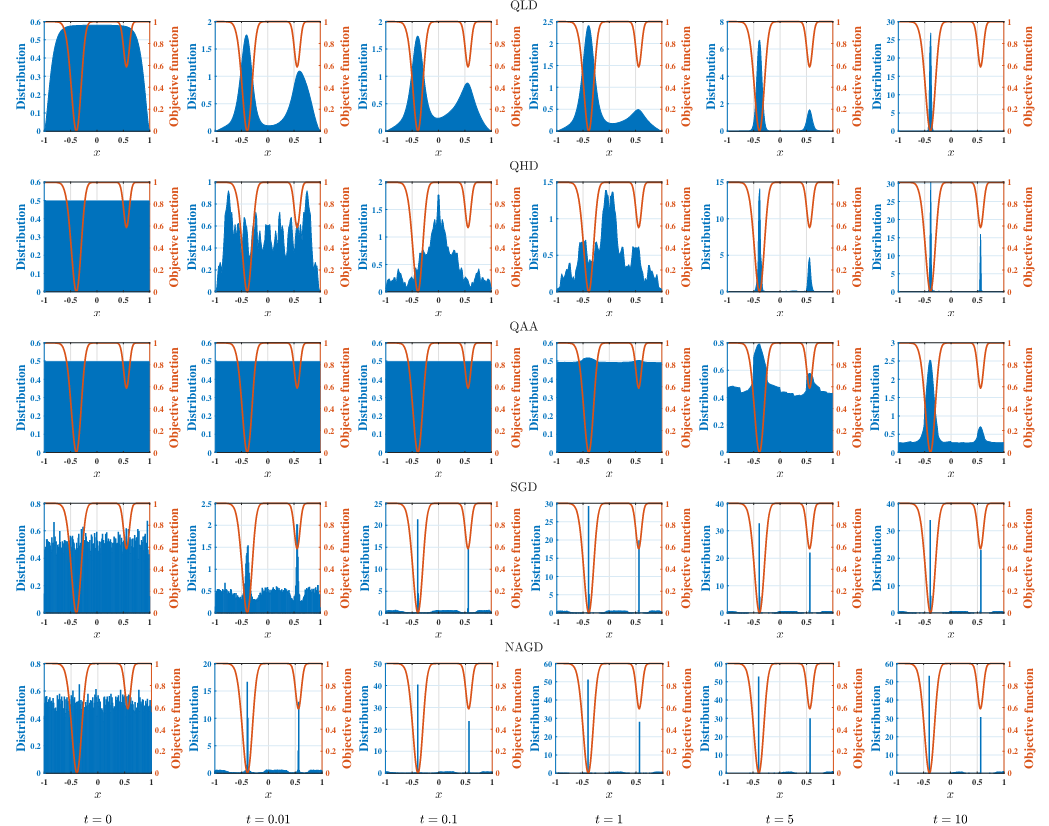
图5. Michalewicz 函数下不同算法的优化过程

结论

本研究展示了 QLD 在优化问题中的潜力，提供了其在一定条件下的收敛性理论保证，并通过数值实验验证了其优势，尤其在参数调控下能优于其他算法。这项工作从开放量子系统的角度上探索了利用量子物理系统设计优化算法的可能性，通过物理参数的配置最大化量子力学在优化中的作用。

参考文献

[1] Jiaqi Leng, Ethan Hickman, Joseph Li, and Xiaodi Wu, Quantum Hamiltonian descent, arXiv preprint arXiv:2303.01471 (2023).
[2] Shiwu Gao, Dissipative quantum dynamics with a Lindblad functional, Physical Review Letters 79 (1997), no. 17, 3101.
[3] Moritz Hardt, Tengyu Ma, and Benjamin Recht, Gradient descent learns linear dynamical systems, The Journal of Machine Learning Research 19 (2018), no. 1, 1025–1068.

图文 | 陈哲睿陆宇晨

PKU QUARK Lab

关于量子算法实验室

量子算法实验室 QUARK Lab (Laboratory for Quantum Algorithms: Theory and Practice) 由李彤阳博士于2021年创立。该实验室专注于研究量子计算机上的算法，主要探讨机器学习、优化、统计学、数论、图论等方向的量子算法及其相对于经典计算的量子加速；也包括近期 NISQ (Noisy, Intermediate-Scale Quantum Computers) 量子计算机上的量子算法。

实验室新闻：#PKU QUARK

实验室公众号：

课题组近期动态

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点击“阅读原文”转论文链接

内容中包含的图片若涉及版权问题，请及时与我们联系删除

点赞收藏评论分享到Link

沙发等你来抢

去评论

类似文章

CMP | 基于朗之万动力学的量子优化算法

类似文章

OpenAI神秘项目曝光：cderGPT，用AI加速药物评估

Bye，英伟达！华为NPU，跑出了准万亿参数大模型

智源研究院发布开源中文互联网语料库CCI 4.0 新增高质量英文数据与合成数据

评论