当ChatGPT-o3以近乎博士生水平解答各类难题,当DeepSeek-R1在复杂推理任务中超越顶尖工程师,我们惊叹于大模型“智能涌现”的奇迹,然而鲜有人意识到:这些拥有千亿参数的“数字大脑”,本质上是从初始混沌状态,通过数万小时的反复训练渐渐成形。
这一切的幕后推手,正是看似低调却至关重要的神经网络优化器——它犹如AI训练的“导航算法”,在损失函数构成的崎岖高维地形中,既要躲避陡峭的梯度悬崖,又要穿越平坦的局部高原,最终将模型参数引导至性能最优的“新大陆”。
自20世纪50年代随机梯度下降(SGD)首次提出以来,优化算法经历了多次重要演进。从动量方法如 SGD-M 和 NAG,到自适应方法如 AdaGrad、RMSprop 和 Adam,再到新一代优化器 AdamW 和 RAD 的崛起,优化算法的“演变之战”已持续超过70年。本文将梳理主流神经网络优化器的发展历程,帮助读者根据任务特征和需求,选择最合适的优化器,推动实践中的成功应用。
Stochastic Gradient Descent(SGD) [1]
SGD的核心特征在于每次更新时随机选取一个小批量样本(而非整个数据集)来计算梯度。
算法优势
(1)利用小批量更新,较梯度下降计算量大幅降低,适合处理大规模数据集。
(2)使用随机梯度,有助于跳出局部最优解,从而提高找到全局最优解的可能性。
算法挑战
(1)随机梯度序列的方差可能较大,从而导致训练过程的不稳定性。
(2)损失函数非凸,SGD仍可能陷入鞍点或局部极小值。
(3)对于条件数较大的问题,固定学习率可能效果不佳,易导致收敛缓慢或不收敛。
Stochastic Gradient Descent with Momentum(SGD-M)[2]
不同于SGD直接使用当前时刻的随机梯度\( \nabla J(\theta_k) \)作为期望梯度\( g_k \),SGD-M使用动量\( v_k \)与\( \nabla J(\theta_k) \)的加权平均作为\( g_k \),其中加权系数为动量系数\( \beta \)。这实际上是对历史所有随机梯度{\( \nabla J(\theta_0),...,\nabla J(\theta_k) \)}的指数移动平均。
在图1中,左图展示了SGD算法的梯度下降过程,存在较大震荡,且未能朝向最优解更新;右图则展示了SGD-M的单步梯度下降过程,其中红虚线代表\( \nabla J(\theta_k) \)的分量,蓝虚线代表\( v_k \)的分量,绿色实线表示经过动量修正后实际用于参数更新的梯度\( g_k \)。通过比较,可以看到修正后的梯度方向更趋向于最优解,震荡得到有效抑制。
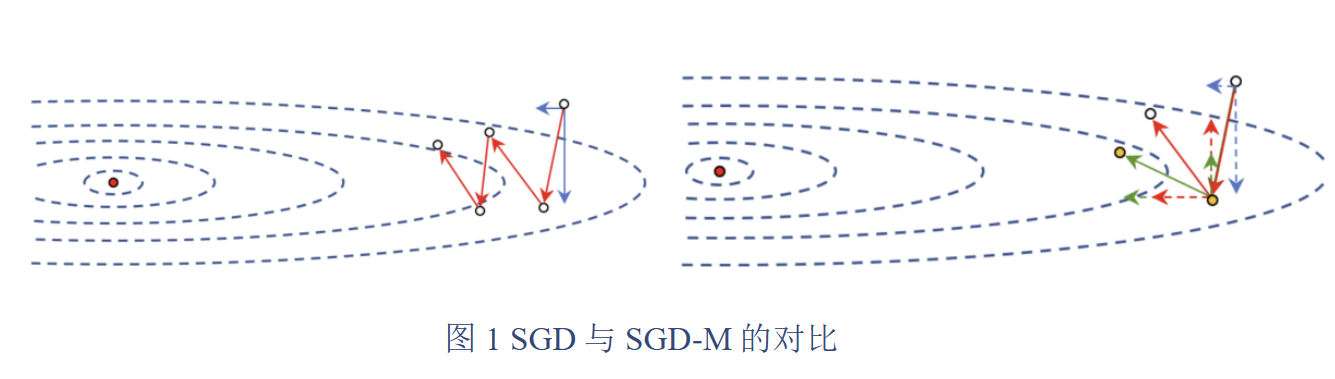
算法优势
(1)在损失函数曲率较低(即梯度方向一致)的区域,动量项通过累积梯度,能够加快参数更新速度。
(2)在损失函数曲率较高(即梯度方向变化较大)的区域,动量项有助于平滑更新方向,减小震荡。
(3)动量项的累积效应能够帮助算法跳出局部最优解,非凸优化问题中尤为有效。
算法挑战
(1)由于动量项的累积效应,SGD-M可能在接近最优解时产生超调,从而错过最优解。
(2)当梯度估计的噪声较大(如在小批量样本或噪声数据上),动量项可能放大噪声,导致更新方向的不稳定性。
Nesterov Accelerated Gradient(NAG)[3]

NAG通过超前参考未来的信息,使用\( \tilde{\theta_k} \)代替\( \theta_k \)来计算梯度。如图2所示,左图中,红实线表示当前梯度\( \nabla J(\theta_k) \),蓝实线表示动量\( v_k \),黄虚线+黄点表示SGD-M的更新步;中图中,蓝实线上的红点代表超前信息位置\( \tilde{\theta_k} \),红虚线表示在该超前位置处的梯度\( \nabla J(\tilde{\theta_k}) \);右图中,黄虚线+红点表示NAG的更新步,更新方向更趋近于最优解。

算法优势
(1)通过前瞻性更新,更准确地调整更新方向,从而加快收敛速度。
(2)前瞻性机制能够帮助算法跳出局部最优解,特别是在非凸优化问题中尤为有效。
算法挑战
(1)对学习率和动量系数等超参数敏感,手动调参过程复杂。
(2)代码实现稍显复杂,因为需要在预测位置计算梯度。
Adaptive Gradient(AdaGrad)[4]

AdaGrad通过累积梯度平方\( (\nabla J(\theta_k))^2 \)作为二阶动量\( y_{k+1} \),并将其作为期望梯度\( g_k \)的标准化分母,从而动态调整有效学习率\( \alpha_k \)。
算法优势
(1)根据梯度方差动态调整学习率:在梯度方差较大的方向,减缓学习率;而在梯度方差较小的方向,加大学习率,从而促进神经网络在非凸优化问题中的收敛。
算法挑战
(1)二阶动量\( y_{k+1} \)会不断累积,其值可能爆炸,导致有效学习率\( \alpha_k \)收敛到零,学习过程停滞。
Root Mean Square Propagation(RMSProp)[5]

RMSProp通过指数加权移动平均估计期望平方梯度,从而避免了二阶动量持续积累导致学习率衰减为零的问题。
算法优势
(1)通过逐步衰减平方梯度的历史信息,避免了学习率快速衰减的现象,从而在训练过程中保持更稳定的学习率。
(2)根据梯度的历史信息自动调整每个参数的学习率,使得不同参数的学习率可以独立变化。
算法挑战
(1)对初始学习率的选择较为敏感,若初始学习率设置不当,可能导致收敛速度较慢或性能下降。
(2)由于缺乏一阶动量项, RMSProp的收敛速度可能不如结合动量的优化算法。
Adaptive Moment Estimation(Adam)[6]

Adam将RMSProp和Momentum方法结合,通过指数移动平均同时应用于一阶动量\( v_{k+1} \)和二阶动量\( y_{k+1} \)使用两者分别估计梯度的期望(一阶原始矩)和二阶原始矩。同时,Adam引入了偏差校正技术,修正了动量零初始化所引发的估计偏差。
算法优势
(1)通过维护一阶动量和二阶动量,Adam可以高效调整参数更新方向并自动调整有效学习率,加速网络收敛。
(2)对一阶动量和二阶动量进行偏差校正,消除了初始阶段的估计误差,使得参数更新更加准确。
(3)对超参数选择较为鲁棒,通常无需精细调参即可获得较好的性能。
算法挑战
(1)在某些任务中,Adam取得的最终性能可能不如精细调参的SGD或SGD-M。
(2)由于需要存储一阶动量和二阶动量,训练大模型(参数极多)时,显存开销较大。
Nesterov-accelerated Adaptive Moment Estimation(Nadam)[7]

Nadam在Adam的基础上引入了Nesterov加速技术,通过估计未来梯度来更新动量。
算法优势
(1)结合了Nesterov动量法的前瞻性更新机制,使得更新方向更为准确,减少了梯度更新中的震荡,从而加快了收敛速度。
(2)继承了Adam的自适应学习率机制,能够根据梯度的一阶动量和二阶动量动态调整每个参数的更新方向和步长。
(3)对一阶动量和二阶动量进行了偏差校正,消除了初始阶段的估计偏差,使得参数更新更加准确。
算法挑战
(1)Nesterov动量的前瞻性更新机制需要额外计算,因此Nadam的计算开销还要高于Adam。
(2)在训练数据有限或模型未正则化时,可能导致过拟合。
Adaptive Moment Estimation with Weight Decay (AdamW)[8]

AdamW直接在权重上实现weight decay,而非像传统方法那样修改当前梯度,从而避免干扰Adam的矩估计步骤。
Weight decay 技术的核心思想是在优化目标函数中加入\( L2 \)正则项以减弱过拟合,传统做法是通过改变目标函数来调整随机梯度\( \nabla J(\theta_k) \)。AdamW则通过直接在梯度下降步骤中对权重进行衰减,实现了等效的\( L2 \)正则化。
算法优势
(1)通过解耦权重衰减,避免了Adam中权重衰减与自适应学习率之间的冲突,从而提高了模型的泛化能力。
算法挑战
(1)对强化学习可能不适用:通常强化学习任务训练集与测试集相同,对权重的限制可能降低模型的拟合能力,进而导致最终策略的非最优性。
Relativistic Adaptive Gradient Descent(RAD)[9]

RAD将神经网络参数的离散优化过程对偶为耗散动力学系统状态的离散演化过程,为主流加速梯度和自适应优化算法提供了动力学解释。通过速度系数\( \delta \)和保辛因子\( \zeta \)控制梯度标准化程度与学习率自适应力度,RAD有效抑制了异常梯度的影响,特别适用于强化学习等深度学习任务。
算法优势
(1)RAD具有完备的理论基础和动力学根源,具有更强的可解释性。
(2)网络参数独立自适应调节,随机非凸优化下收敛速度快。
(3)自然限制网络参数的更新步长,有效避免异常梯度的影响,训练稳定性强。
(4)利用保辛退火机制,在训练初期允许网络快速更新至次优参数空间,在训练后期稳定搜索到最优解。
算法挑战
(1)保辛因子序列需根据任务特征和训练需求进行人工设计,以获得最佳性能。
算法特性总结
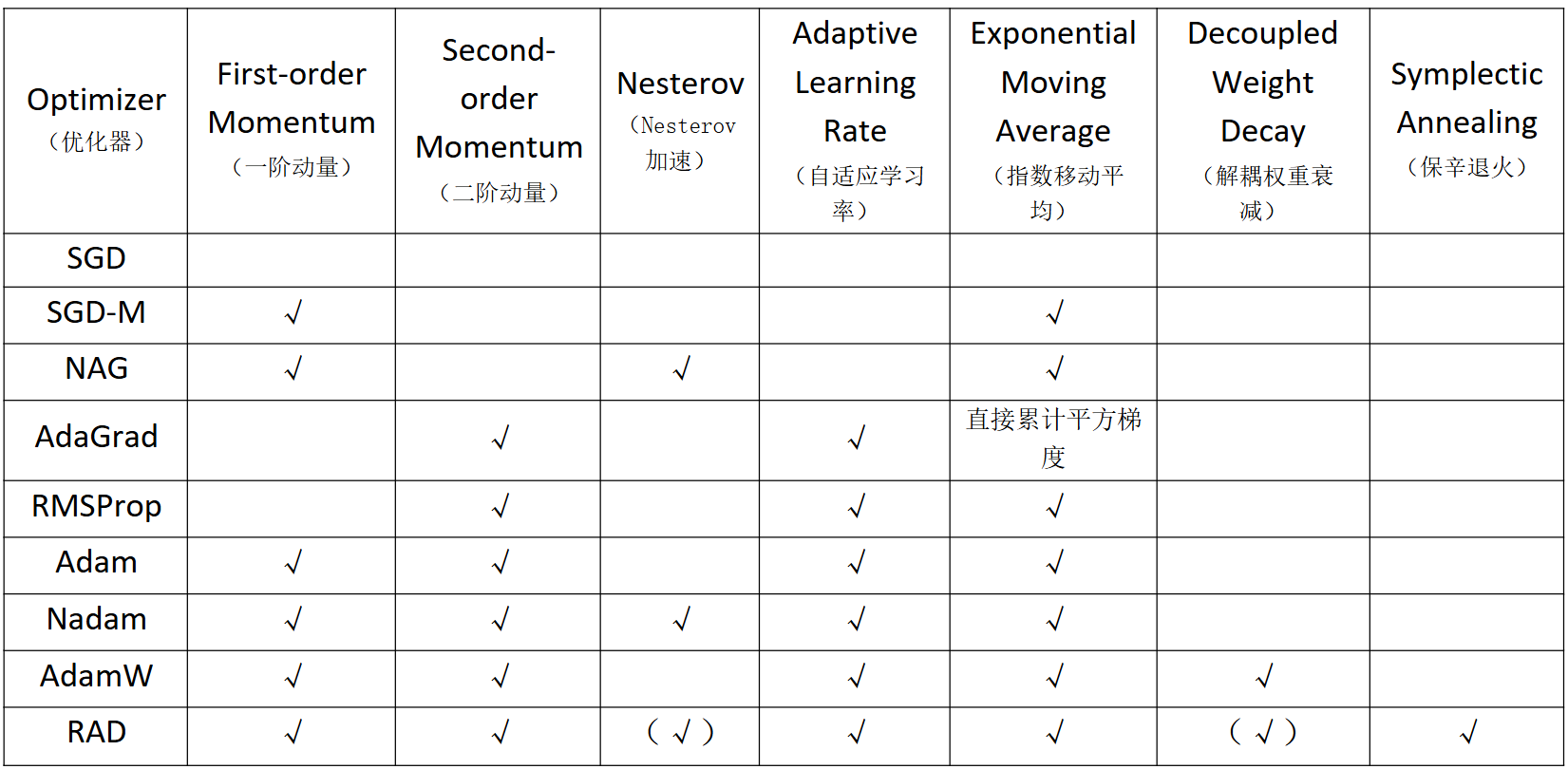
*(√)表示技术可启用
参考文献
[1]Robbins, H., & Monro, S. (1951). A stochastic approximation method. The Annals of Mathematical Statistics, 22(3), 400-407.
[2]Polyak, B. T. (1964). Some methods of speeding up the convergence of iteration methods. U.S.S.R. Computational Mathematics and Mathematical Physics, 4(5), 1–17.
[3]Nesterov, Y. (1983). A method of solving a convex programming problem with convergence rate O(1/k^2). Soviet Mathematics Doklady, 27(2), 372–376.
[4]Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of machine learning research, 12(7), 2121–2159.
[5]Hinton, G., Srivastava, N., & Swersky, K. (2012). Lecture 6a overview of mini–batch gradient descent. Coursera Lecture slides https://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf [Online].
[6]Kingma, D. P., & Ba, J. (2015). Adam: A method for stochastic optimization. Proceedings of the 3rd International Conference on Learning Representations (ICLR) 2015, San Diego, CA, USA, May 7-9, 2015.
[7]Dozat, T. (2016). Incorporating Nesterov Momentum into Adam. Proceedings of the 4th International Conference on Learning Representations, Workshop Track.
[8]Loshchilov, I., & Hutter, F. (2019). Decoupled weight decay regularization. In 7th International Conference on Learning Representations (ICLR) 2019, New Orleans, LA, USA, May 6-9, 2019.
[9]Lyu, Y., Zhang, X., Li, S. E., et al. (2024). Conformal Symplectic Optimization for Stable Reinforcement Learning. IEEE Transactions on Neural Networks and Learning Systems. doi: 10.1109/TNNLS.2024.3511670.
内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢