春分 | QSP/QSVT与切比雪夫多项式

量子优势得益于量子力学规则；量子计算模型也受限于量子力学规则。相比于设计经典算法，设计量子算法有更多的掣肘，是带着镣铐跳舞。许多量子算法只能解决特定的问题，这些问题的形式相对特殊，没有或很少触碰到量子计算模型的能力界限。为了将量子计算推向实际应用，人们开始尝试触碰这些界限，设计更通用、解决更一般问题的量子算法，HHL 就是其中一个代表。虽然 HHL 并不完美，但人们的想法开始萌芽：探索求解线性代数、动力系统等较为普遍的数学问题的量子算法，以期量子计算在未来，以可调用的数值求解器的形式，助力通用科学计算、机器学习等重计算负担的应用。

QSVT 是当代量子算法的重要成果，它能在量子计算机上处理一些较为普遍的线性代数问题，比如矩阵逆、特征值分析等^[1]。有人称 QSVT 是许多量子算法的“大一统”^[2]。

QSVT 使用了单变量 QSP 作为子例程。下面将介绍 QSP，QSVT，以及它们背后的一个数学工具：切比雪夫多项式。

QSP 是一条流水线，里面装着旋转门（rotation gates）和信号门（signal gates）。通过巧妙地组合这些门，我们可以构造一个酉算符，这个算符在某个子空间上的投影可以用一个多项式来表示。简单来说，QSP 能让我们在量子计算机上实现一些数学函数的近似，而且这些函数通常是多项式形式的。

QSVT 是一座 QSP 大工厂。QSP 是对单个信号进行处理，QSVT 则是对矩阵的奇异值（singular values）进行变换。它的核心思想是把 QSP 推广到更高维度，用 Qubitization 技术访问块编码子空间，对矩阵的奇异值作用某个函数。

图1. 来自 Pennylane^[3]的可爱手绘

单变量 QSP 的形式如下^[4]：

$S(\phi_0) \prod_{k=1}^{d} W(a) S(\phi_k) = \begin{pmatrix} P(a) & i Q(a) \sqrt{1 - a^2} \\ i Q^*(a) \sqrt{1 - a^2} & P^*(a) \end{pmatrix}$ $W(a)$ 是一个信号门：

$W(a) = \begin{pmatrix} a & i \sqrt{1 - a^2} \\ i \sqrt{1 - a^2} & a \end{pmatrix}$ $S(\phi) = e^{i \phi Z}$ 是一个旋转门， $Z$ 是 Pauli-Z。这个等式的右边是一个矩阵，包含了两个多项式 $P(a)$ 和 $Q(a)$ ，它们需要满足一些条件：

度数不超过 $d$ （对于 $P$ ）和 $d-1$ （对于 $Q$ ）；
奇偶性要求： $d \mod 2$ （对于 $P$ ）和 $d-1 \mod 2$ （对于 $Q$ ）；
单位性条件： $|P(a)|^2 + (1 - a^2) |Q(a)|^2 = 1$ 。

通过调整参数 $\phi_0, \phi_1, \ldots, \phi_d$ ，我们可以用量子门的序列生成特定的多项式 $P(a)$ 。

QSVT 的泛用性归功于背后的数学工具。其中一个重要的数学工具是切比雪夫多项式。它们是一类特殊的正交多项式，用处是函数逼近：

$T_n(\cos \theta) = \cos (n \theta)$ 其中， $n$ 是一个非负整数， $\theta$ 是实数。可验证递推关系

$T_{n+2}(x) = 2x T_{n+1}(x) - T_n(x)$ 为什么切比雪夫多项式这么特别？切比雪夫多项式有几个好的性质：

1. 正交性：在区间 $[-1, 1]$ 上，定义一个内积：

$\langle f, g \rangle = \int_{-1}^{1} \frac{f(x) g(x)}{\sqrt{1 - x^2}} \, dx$ 可以验证切比雪夫多项式在这个内积下是正交的。对于 $\sqrt{\frac{1}{\pi}}T_0\$ ， $\sqrt{\frac{2}{\pi}} T_k$ , $k >0$ ，它们甚至是正交归一的。这意味着它们像一组“互相垂直”的基矢量，可以用来分解函数。

2. 逼近能力：任何 $[-1, 1]$ 上的解析函数 $f(x)$ 都可以写成切比雪夫级数：

$f(x) = \sum_{k=0}^{\infty} a_k T_k(x)$ 系数 $a_k$ 通过内积计算：

$a_0 = \frac{1}{\pi} \int_{-1}^{1} \frac{f(x)}{\sqrt{1 - x^2}} \, dx, \quad a_k = \frac{2}{\pi} \int_{-1}^{1} \frac{f(x) T_k(x)}{\sqrt{1 - x^2}} \, dx \ (k >0)$ 在实际中，我们不可能用无限项的级数，所以会截断到有限项，得到一个多项式逼近：

$f(x) \approx \sum_{k=0}^{n} a_k T_k(x)$ 这时候，误差（也就是忽略的后面那些项）有多大就很重要。切比雪夫多项式厉害的地方在于，它的系数 $a_k$ 通常很快衰减，因此很快逼近，误差可以控制得很小。这是 approximation theory 研究的结果^[6]。

QSP 的目标是构造一个多项式 $P(a)$ ，让它尽可能接近某个目标函数 $f(a)$ ，并且这个多项式可以通过量子门的序列实现。这种任务本质上是一个多项式优化问题。而切比雪夫多项式正是解决这个问题的利器。

其原因在于，切比雪夫多项式是正交的，而且它们在 $[-1, 1]$ 上有很好的逼近性质。回到 QSP， $P(a)$ 的度数不超过 $d$ ，并且需要满足单位性条件。切比雪夫多项式可以作为构建 $P(a)$ 的基础，因为它们天然满足一定的度数和奇偶性要求（比如 $T_n(x)$ 的度数是 $n$ ，奇偶性与 $n \mod 2$ 一致）。

举个例子：假设我们想用 QSP 实现一个简单的函数，比如 $f(a) = a^2$ 。我们可以尝试用切比雪夫多项式逼近它。注意到 $T_2(a) = 2a^2 – 1$ ，微调一下， $\frac{T_2(a) + 1}{2} = a^2$ 。这说明，通过线性组合切比雪夫多项式，我们可以构造出目标函数的多项式形式，然后通过QSP的框架找到对应的 $\phi_k$ 参数。

QSVT 的目标是对一个矩阵 $A$ 的奇异值应用函数 $f(\cdot)$ 。假设 $A = U \Sigma V^\dagger$ 是奇异值分解， $\Sigma$ 是奇异值矩阵，我们想计算 $f(\Sigma)$ 。QSVT 通过一系列量子操作（基于 QSP 的旋转和投影），将这个函数应用到奇异值上。而这个函数 $f(\cdot)$ ，就用上面的技术来近似。

读者可能已经注意到，前面只在实数上介绍了切比雪夫多项式的性质。为了让这个工具真正适配量子计算，需要把这些好性质扩展到复数上。

复数上的形式：

$T_n\left( \frac{1}{2}(z + z^{-1}) \right) = T_n(\cos \theta) = \cos n\theta = \frac{1}{2}(e^{in\theta} + e^{-in\theta}) = \frac{1}{2}(z^n + z^{-n})$ 显式公式：

$T_n(x) = \frac{1}{2} \left( (x + \sqrt{x^2 - 1})^n + (x - \sqrt{x^2 - 1})^n \right)$ 这表明 $T_n(x)$ 是 $n$ 次多项式，且在复数域上也成立，其对称性消除了复平方根的歧义，使其始终为多项式。

参考 [5] 中的思路，接下来展示：在复数上，切比雪夫多项式的系数也能够保持好的衰减性质，从而可以高效逼近。

解析延拓：对于一个在 $[-R, R]$ 上解析的函数 $f(x) = \sum_{k=0}^\infty c_k x^k$ ，其解析延拓到复平面上的圆盘 $D_R = \{ z \in \mathbb{C} \mid |z| < R \}$ 为：

$f(z) = \sum_{k=0}^\infty c_k z^k$ 这在 $( |z| < R )$ 内绝对收敛。

对于切比雪夫多项式，用环面 $A_R = \{ z \in \mathbb{C} \mid R^{-1} \leq |z| \leq R \}$ 和椭圆 $E_R$ （由 $x = \frac{1}{2}(z + z^{-1})$ 将 $A_R$ 映射得到的区域）。如果 $f(x)$ 在 $E_R$ 上解析，定义：

$F(z) = f\left( \frac{1}{2}(z + z^{-1}) \right)$ 其中 $a_k$ 是 $f$ 在 $[-1, 1]$ 上的切比雪夫系数：

- $a_0 = \frac{1}{\pi} \int_{-1}^1 \frac{f(x) T_0(x)}{\sqrt{1 - x^2}} \, dx$ ，

- $a_k = \frac{2}{\pi} \int_{-1}^1 \frac{f(x) T_k(x)}{\sqrt{1 - x^2}} \, dx$ （ $k >0$ ）。

插入前面复数版本的形式，然后做柯西积分：

- $a_0 = \frac{1}{2\pi i} \int_{|z|=R} \frac{F(z)}{z} \, dz$ ，

- $a_k = \frac{1}{\pi i} \int_{|z|=R} \frac{F(z)}{z^{k+1}} \, dz$ （ $k >0$ ）。

用留数定理可以快速验证这些积分：

接下来，我们将分析系数的衰减速度。

若 $f$ 在 $E_R$ 上有界，即 $|f(z)| \leq M$ （记为 $\|f\|_{E_R} = M$ ），则^[8]：

$\left| a_k \right| = \left| \frac{1}{\pi i} \int_{|z|=R} \frac{F(z)}{z^{k+1}} \, dz \right| = \left| \frac{1}{\pi} \int_0^{2\pi} \frac{F(R e^{i\theta})}{(R e^{i\theta})^k} \, d\theta \right| \leq \frac{1}{\pi} \int_0^{2\pi} \frac{|F(R e^{i\theta})|}{R^k} \, d\theta \leq \frac{2M}{R^k}$ 我们看到 $a_k$ 随 $k$ 增加呈指数衰减，衰减速度与 $R^k$ 成反比。这在量子算法（如 QSP 和 QSVT）中至关重要，因为它保证了低阶多项式逼近的高效性，从而可以节约量子门。

举个例子： $f(x) = e^x$

对于 $f(x) = e^x$ （在整个复平面解析）。令 $M = \max_{z \in E_R} |e^x|$ ，其中 $x = \frac{1}{2}(z + z^{-1})$ ，且 $R^{-1} \leq |z| \leq R$ 。由于：

$|e^x| = e^{\text{Re}(x)} \leq e^{\frac{1}{2}(|z| + |z^{-1}|)} \leq e^{\frac{1}{2}(R + R^{-1})}$ 取 $R >1$ ，最大值在 $|z| = R$ 时达到 $e^R$ 。故：

$|a_k| \leq \frac{2 e^R}{R^k}$ 优化 $R$ ，令 $h(R) = \frac{2 e^R}{R^k}$ ，其导数为零时 $R = k$ ，代入得：

$|a_k| \leq 2 \left( \frac{e}{k} \right)^k$ 这接近 Stirling 公式的逆，说明 $a_k$ 衰减极快。

QSVT 背后的有趣数学工具还有很多。前面的段落介绍了单变量 QSP 操作背后的数学工具。而从单变量到矩阵，需要做 qubitization：借助 Jordan's Lemma 或者 Cosin-Sin Decomposition 等工具，像操作单个变量一样操作矩阵的特征值，从而可以对厄米矩阵的特征值或非厄米矩阵的奇异值做变换。QSP 也发展出了多变量版本^[7]：使用 Fejér-Riesz Theorem 等工具，支持更复杂的多变量多项式变换，高效计算某些依赖多个变量的属性。

回到前文，作为量子算法的“大一统”，我们可以通过挑选合适的 $f(\cdot)$ 来用 QSVT 实现各种量子算法的功能。

哈密顿模拟：也就是在量子计算机上模拟动力系统演化，也就是近似 $f(x)=e^{ixt}$ 。QSVT 在此的应用是最优的。技术上，为了满足奇偶性要求，使用 $\sin(xt)$ 和 $\cos(xt)$ 的组合来近似 $f(x)=e^{ixt}$ ， $\sin(xt)$ 和 $\cos(xt)$ 可以由 Jacobi-Anger Expansion 表示为切比雪夫多项式的和，从而调用 QSP 近似这些切比雪夫多项式。最后，做振幅放大，来提升模拟的精度^{[1, 4]}。

再简单列举其他的：

无结构搜索：目标是近似 $f(x)= sign(x-c)$ 。奇异值 $a = 1/\sqrt{N}$ 与初始态和标记态相关。设置 $c$ 使得 $a >c$ 。这样把标记态的振幅变换到1。

线性方程组求解：目标是近似 $f(x)=1/x$ 。但是注意要适当的逼近函数，需要足够接近 $1/x$ ，且避免 $x=0$ 时的奇点问题，且平滑。

相位估计：目标是近似 $f(x)= sign(1/√2 - x)$ 。这函数用于“剪切”相位，使其符合设置好的精度。

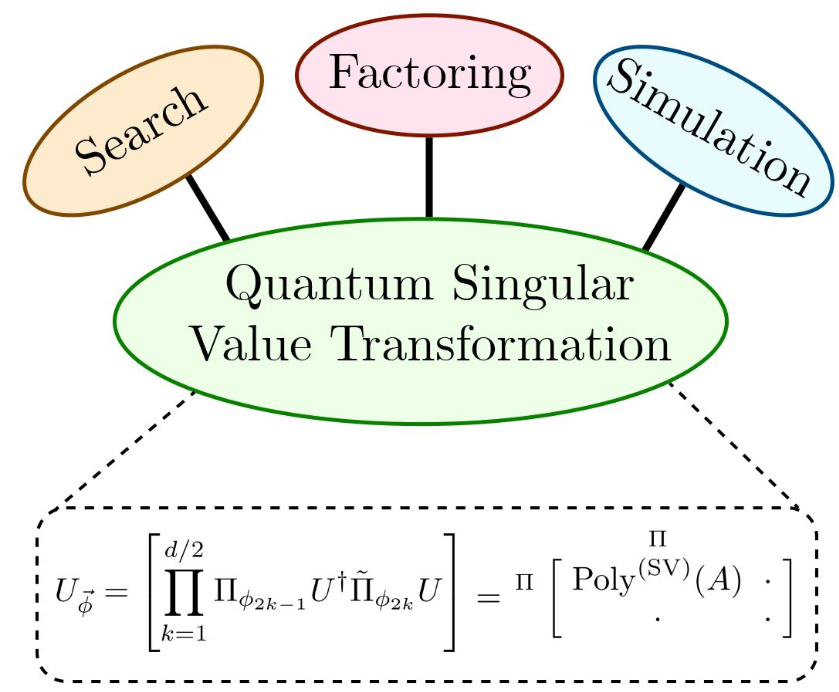
图2. PRX Quantum 刊载版本论文的示意图^[2]

QSVT 之后还有 QEVT，用来处理非正规矩阵，进一步用到了 Chebyshev 母函数等工具^[9]。

最后，笔者提醒大家，近日换季，请大家注意饮食安全，通风换气，以及穿衣保暖。祝大家身体健康。

参考文献：

[1] András Gilyén, Yuan Su, Guang Hao Low, Nathan Wiebe. Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics, In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing (STOC 2019), pp. 193-204

[2] John M. Martyn, Zane M. Rossi, Andrew K. Tan, and Isaac L. Chuang Grand Unification of Quantum Algorithms, PRX Quantum 2, 040203

[3] Juan Miguel Arrazola. https://pennylane.ai/qml/demos/tutorial_intro_qsvt

[4] Guang Hao Low, Isaac L. Chuang. Optimal Hamiltonian Simulation by Quantum Signal Processing

[5] Ewin Tang, Kevin Tian. A CS guide to the quantum singular value transformation. arXiv:2302.14324

[6] Sushant Sachdeva and Nisheeth K. Vishnoi. Faster algorithms via approximation the ory. Found. Trends Theor. Comput. Sci., 9(2):125–210, 2014.

[7] Zane M. Rossi, Isaac L. Chuang. Multivariable quantum signal processing (M-QSP): prophecies of the two-headed oracle

[8] Lloyd N. Trefethen. Approximation theory and approximation practice, extended edition. Extended edition [of 3012510]. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2019, pp. xi+363. isbn: 978-1-611975-93-2.

[9] Guang Hao Low, Yuan Su. Quantum eigenvalue processing

文 | 李天翊

图 | 朱成轩

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

内容中包含的图片若涉及版权问题，请及时与我们联系删除

春分 | QSP/QSVT与切比雪夫多项式

评论