
图机器学习已成为一种强大的工具,用于建模数据实体之间复杂的相互关系。这些方法已应用于从社会科学到分子生物学等多个领域,提供了前所未有的洞察力。然而,一个重大挑战是需要一个明确且准确的图作为输入,而这并不总是能够获得。这促使了图学习(Graph Learning)这一学科的发展,其重点是从图节点上观察到的数据中推断图拓扑结构。
现代图学习面临一些挑战,例如数据集不完整或复杂的拓扑属性难以融入模型规范。为了解决这些挑战,本论文从多个角度研究了基于模型的图学习,并提出了两种新颖的方法:核图学习(Kernel Graph Learning, KGL)和学习图拓扑(Learning to Learn Graph Topologies, L2G)。KGL 从函数视角开发,提供了一个鲁棒的模型,能够通过联合推断图和受图影响的数据分布来处理噪声和缺失的节点数据。另一方面,L2G 采用深度学习架构,将图邻接矩阵的优化转化为参数化函数映射任务,从而确保在具有特定拓扑属性的图学习中实现更快的推理和更高的精度。
在实际应用方面,我们专注于量化金融领域,其中市场、机构和资产之间深度互联。尽管当代金融研究使用图表示来可视化经济联系,但图机器学习的潜力及其增强预测能力的作用却很少被探索。从丰富的数据源中学习金融图也缺乏研究。本论文旨在弥合这一差距。通过从定价数据中学习资产的金融网络,我们改进了投资组合构建,提高了盈利能力。此外,还开发了一种定制的图神经网络模型 GNNHAR,用于研究股权图中的非线性波动溢出效应,并改进已实现波动率的预测。

论文题目:Graph-based Inference and Learning with Applications in Finance
作者:Xingyue (Stacy) Pu
类型:2023年博士论文
学校:University of Oxford(英国牛津大学)
下载链接:
链接: https://pan.baidu.com/s/14qNo2HcwfRbruS-Y4nlZfg?pwd=ziv2
硕博论文汇总:
链接: https://pan.baidu.com/s/1Gv3R58pgUfHPu4PYFhCSJw?pwd=svp5
当我们通过统计插补来解决数据质量问题时,了解图形和数据之间的相互关系非常重要。这种相互交织的关系有两个主要方向——数据分布受图形结构的影响,图形结构从数据实现中推断出来。现有的图形学习公式主要侧重于从底层数据观察中提取图形结构。然而,在数据质量低的情况下,必须认识到,考虑到数据分布和图形拓扑之间的联合关系,图形的固有结构可以相互指导数据推断。这种并发的联合关系通常仍未得到充分探索,这强调了需要一种同时推断图形和数据的新方法。数据和图形之间的这种联合关系提出了数据驱动的图形学习面临的建模挑战。我们在第 2 章中的探索是出于从功能角度理解图形学习的愿望。我们的目标是以一种能够同时推断数据和图表的方式理解和建模联合关系。从函数角度来看,这种联合关系可以通过核函数的线性组合来近似,并用观察到的数据点进行评估。我们在第 2 章中介绍了公式。
除了输入数据之外,文献尚未广泛探讨有关图学习框架的潜在结果(即学习到的图)的某些重要考虑因素。其中一个考虑因素是在结果图上实施灵活的拓扑属性,这些属性超出了通常选择的稀疏性。这种稀疏性已明确集成到许多现有方法的优化问题中,作为附加凸正则化函数[79, 129, 42, 185, 167, 112]。虽然稀疏性无疑是一个重要属性,有助于突出显示结果图中的关键连接,但在学习具有受特定应用领域启发的属性的图中仍有潜力(例如,社区的存在[76],无标度属性[14])。这些属性可能提供显着的优势,值得更深入的探索。然而,它们尚未有效地转化为正则化器以集成到现有的优化框架中。这一差距促使我们探索深度学习方法,利用其通用近似能力。如第 3 章所述,我们提出了一种展开神经网络,该网络具有一层拓扑差异变分自动编码器,以取代传统图学习中的结构正则化函数。通过使用具有相同拓扑特征的图进行训练,我们提出的神经网络有望学习从节点观测到具有预期结构属性的底层图拓扑的映射。
在量化金融应用领域,缺乏现成或有用的图形表示尤为明显。资产,无论是股票、债券、商品还是衍生品,都不是孤立运作的。许多研究强调了金融资产之间关系的存在、重要性和持久性 [48, 83, 94]。它们通过一系列经济、地缘政治和市场驱动因素紧密相连 [48, 156, 164, 123]。例如,同一行业内公司的股价可能会因共同的市场风险而相互影响 [156, 28],一个国家的货币价值可能会影响全球大宗商品市场 [47]。虽然这些成对检查提供了有价值的见解,但它们可能无法完全捕捉互联金融生态系统的复杂动态。此类分析可能会忽视更广泛的网络效应和通过广泛的资产互联网络传播的潜在连锁影响[15]。此外,现代金融研究通常不通过图形表示来表示资产互联,例如图形邻接矩阵或拉普拉斯矩阵。这些矩阵表示通常用作图形机器学习模型的输入。这种疏忽导致了重大的研究空白,忽视了图形机器学习在量化金融中的预测和推理能力。这一空白为探索提供了绝佳的机会。通过创建有效的方法来推断金融图表并利用基于图形的技术,我们可以获得更深入的见解并做出更明智的财务决策。在本文中,我们深入研究了两个量化金融主题,展示了图形机器学习,特别是金融图形学习,如何增强投资组合构建(第 4 章)和风险管理(第 5 章)。
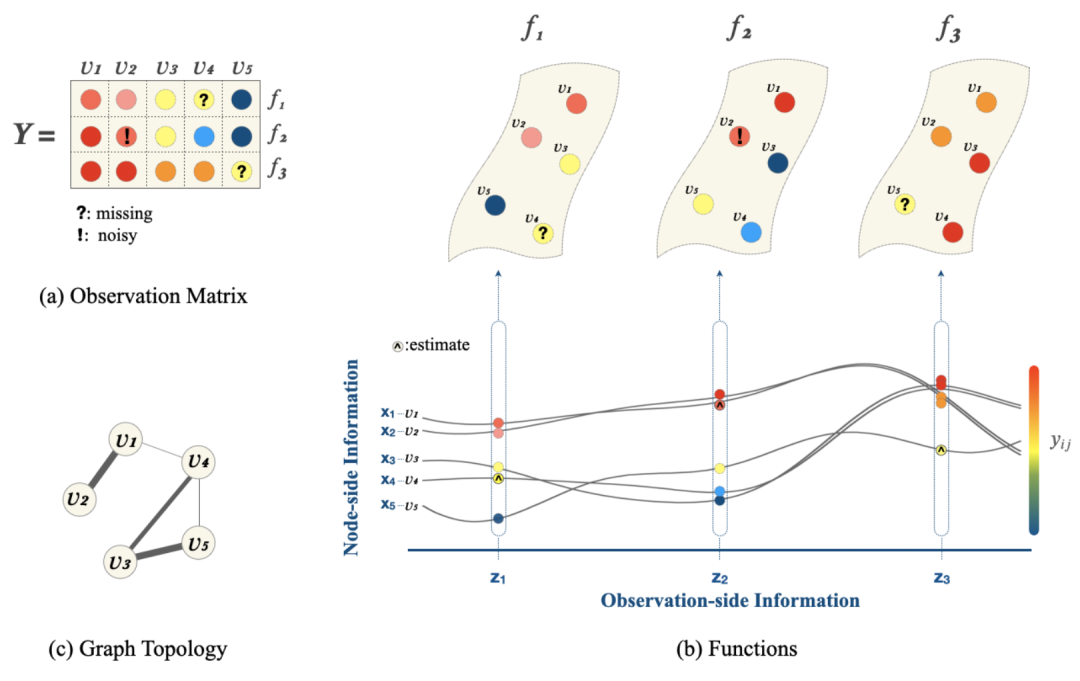
图学习的功能观点。(a)具有缺失和噪声条目的观察矩阵;(b)观察矩阵的每一行都被建模为从底层函数 f(顶部)在一组固定位置(被视为图中的节点)获得的样本;每个节点的值由底层函数以及节点端信息 x 和观察端信息 z(底部)确定;(c)学习到的图拓扑。
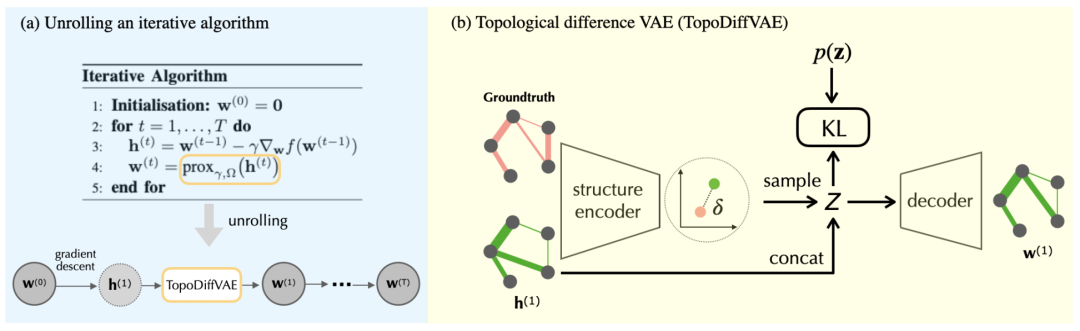
所提议框架的说明。

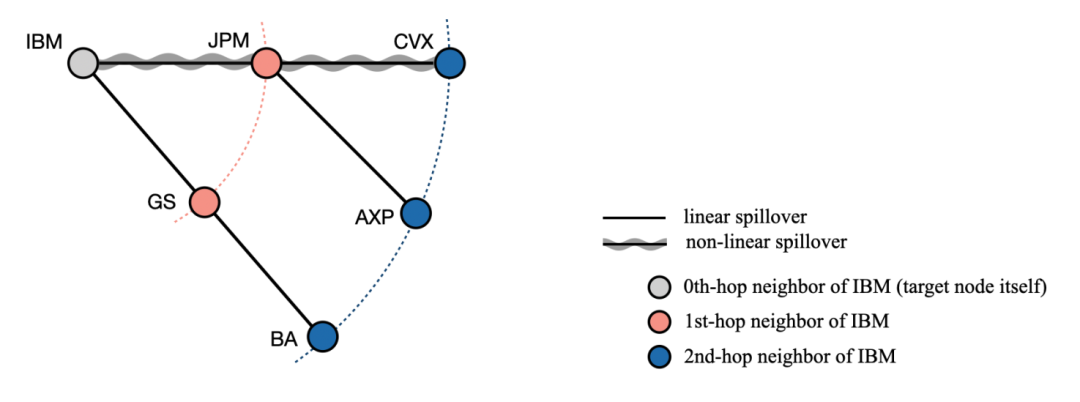
多跳和非线性波动溢出的说明。注:目标节点代表 IBM 的波动性。连接仅用于说明,因此不一定与我们的实验一致。
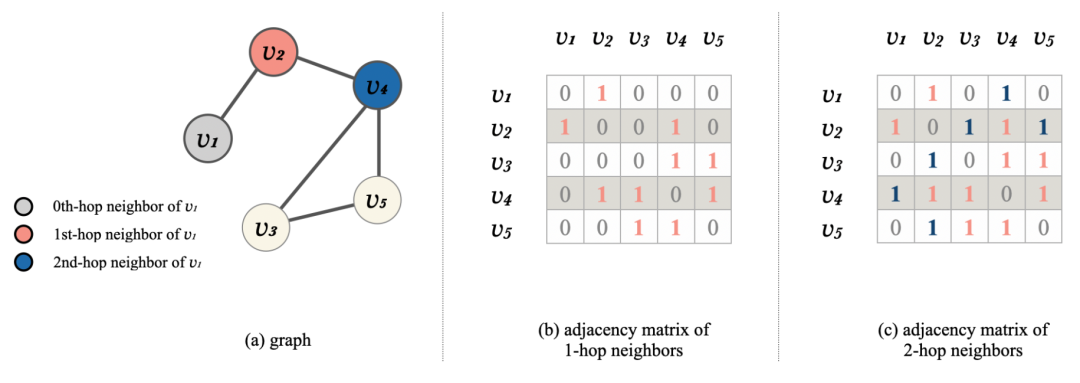
具有多跳邻居的图表及其对应的邻接矩阵的图示。
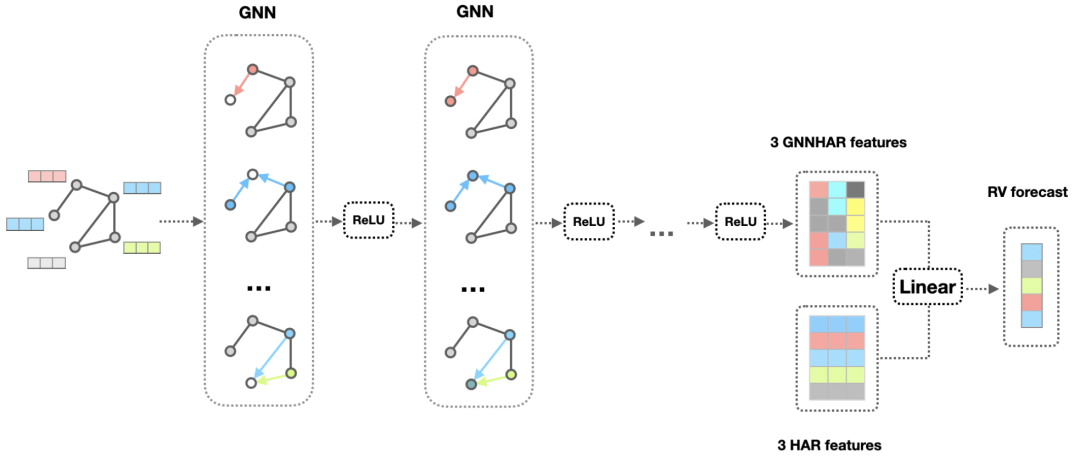
GNNHAR 模型的图示。





内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢