ICLR 2025 | 量子算法求解非凸优化问题的鲁棒性

现有理论研究表明，量子计算机在解决诸多优化问题（如线性规划、半正定规划、凸优化、非凸优化等）方面具有潜在优势。衡量量子优化算法的一个关键方面是其鲁棒性。一方面，当前的量子设备存在硬件噪声，在最坏情况下，这些噪声可能呈对抗性，从而抵消量子算法的优势。另一方面，经典优化问题中固有的噪声同样对算法的鲁棒性提出了挑战。例如，在统计机器学习中，目标函数通常是多个子函数的统计平均，而优化算法往往只能访问子函数的信息，而无法直接获取目标函数的精确值，因此只能对其进行有误差的估计。

在从理论角度分析有噪声的非凸优化问题时，现有的一系列优化理论文献提出了以下模型：尽管算法无法直接获取光滑目标函数  的信息，但它可以访问  的一个有噪声估计  ，且  与  在逐点意义下彼此接近，即

在该模型下，  仍可能是非光滑的，并且可能包含一些  中不存在的浅局部最小值。然而，已有研究表明，可以利用  和  之间的逐点接近性，从而离开仅存在于  中的次优局部最小值，最终找到  的近似局部最小值。

给定一个  维目标函数  ，假设其函数值以及一阶和二阶导数的光滑性存在上界：

模型1：函数值的有噪声估计

存在一个与  在逐点意义上接近的有噪声估计  ，满足  ，并且我们可以访问一个存有  函数值的量子黑盒： 模型2：梯度的有噪声估计

存在一个与  在逐点意义上接近的有噪声估计  ，满足  , 并且我们可以查询一个存有  梯度值的量子黑盒： 

在本文中，我们系统地研究了带噪声的非凸优化量子算法。在模型1和模型2中，我们识别并分析了不同的参数空间，量子算法在这些空间中分别能够以多对数、多项式或指数级的查询次数，找到  -近似局部最优解。同时，我们用信息论证明，存在一个参数空间，即使允许无限次查询，也无法找到  -近似局部最优解。

在某些设定下，我们进一步建立了经典算法的查询复杂度下界，并设计了相应的量子算法，其在查询复杂度上相较于经典下界或当前最先进的经典算法实现了多项式或指数级的加速。我们在表1和表2中分别汇总了模型1和模型2下的主要结果。

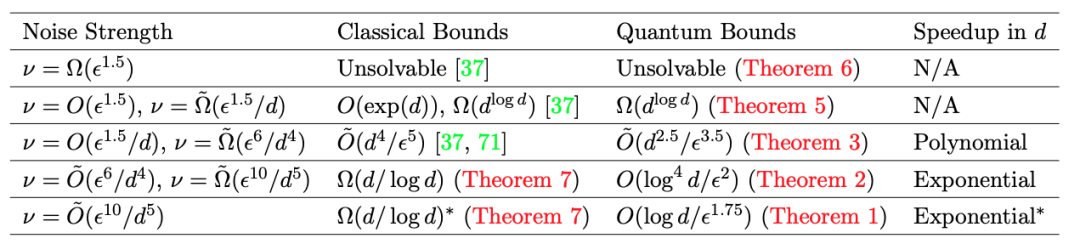
表1. 模型1中的主要结果，以及与当前最先进的经典算法上界和下界的对比。查询复杂度以维度  和精度  为参数进行标注。

表2. 模型2中的主要结果，以及与当前最先进的经典算法上界和下界的对比。查询复杂度以维度  和精度  为参数进行标注。

接下来，我们简要介绍模型1下针对不同噪声层级的算法设计思路。

微小噪声：扰动加速梯度下降的鲁棒性

已有研究^[1]表明，当梯度存在误差时，扰动加速梯度下降算法（PAGD）^{[2, 3]}的性能仍然得以保持。我们严格证明了，结合 Jordan 提出的量子梯度估计算法^[4]，算法^[3]在函数值量子黑盒存在微小噪声  的情况下依然具有鲁棒性，其收敛性不会受到影响。我们进一步证明，这种鲁棒性是量子算法所特有的：任意的经典算法都存在一个多项式级的查询下界。因此，量子算法在这一参数空间中具有指数级的优势。

较小噪声：量子梯度估计的鲁棒性

当噪声强度增大时，扰动加速梯度下降（PAGD）中的负曲率估计部分将失效。在这种情况下，我们展示了结合量子梯度估计的扰动梯度下降算法对噪声的鲁棒性。已有文献^{[5, 6]}从概念层面指出，结合 Jordan 提出的梯度估计方法^[4]的扰动梯度下降算法（PGD）^[7]对噪声具有一定的鲁棒性。在本文中我们证明，在函数值量子黑盒存在较小噪声  ，  时，量子算法可以在  次查询内找到  -近似局部最优解。类似地，这种鲁棒性仅存在于量子算法中，并在查询复杂度上相较于经典算法实现了指数级的量子加速。

中等噪声：基于量子均值估计的加速

当噪声强度进一步增加到  ，  时，Jordan 算法的鲁棒性也不足以应对带噪函数  与目标函数  之间的差异。为了解决这一问题，我们借鉴文献^[8]的思路，基于对  的高斯平滑，设计了一种新的量子算法。我们考虑满足假设1的函数对  。具体地，我们对从高斯分布  中采样得到的值  进行采样^[9]，并利用量子均值估计技术，从这些随机梯度样本中近似重构目标函数的梯度。我们证明，在这一参数空间中，量子算法只需多项式数量的查询即可找到  的一个  -近似局部最优解。回顾最先进的经典算法^[8]，在相同的噪声强度下需要  次查询，我们的量子算法在维度  和精度  两个方面均相较经典结果实现了多项式级的改进。

接下来，我们简要介绍模型1下针对较大噪声层级的复杂度下界构造思路。我们借鉴文献^[8]的方法构造了一个困难实例（图1）：我们在一个超立方体内定义目标函数  ，并利用该超立方体平铺整个空间  。通过在函数值量子黑盒中加入噪声，可以抹去关于  的信息，从而使得在查询次数受限的情况下，无论是经典算法还是量子算法，都无法以高概率找到任何  -近似局部最优解。

在噪声较大，达到  时，我们证明任何量子算法都需要进行至少拟多项式次查询才能找到  -近似局部最优解。为证明该下界，我们在一个超球  内定义目标函数  ，并将该超球嵌入到一个超立方体中，从而可以覆盖整个空间。接着，我们引入噪声构造函数  ，使得在原点附近形成一个“无信息区域”，即对该区域的任何查询都无法获得关于目标函数  的任何局部最优解的信息。随后，我们将该优化问题转化为一个无结构搜索问题，最终通过应用无结构搜索的量子下界，得到非凸优化问题的查询复杂度下界。

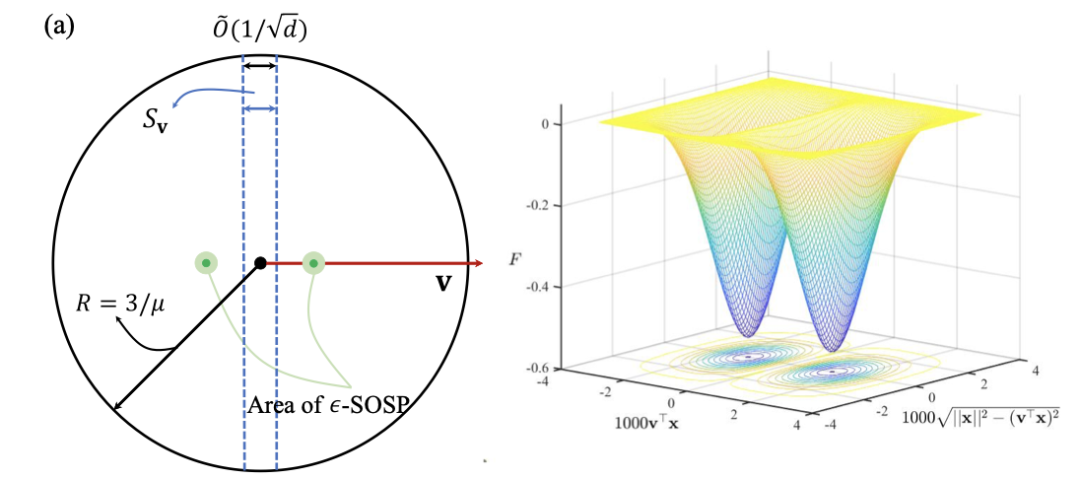
图1. 困难实例的表示图

我们的工作引出了若干值得进一步探讨的开放问题：

（1）是否可以设计更高效的量子算法，用于解决在带噪声量子黑盒模型下的非凸优化问题？例如，能否在维度  和精度  的依赖上进一步改进量子算法的复杂度？

（2）是否可以建立更紧的量子查询下界以刻画非凸优化问题的复杂度？尤其是，对于一般的优化问题（无论使用无噪声还是带噪声的量子黑盒），是否可以建立在维度  上具有次线性或多对数量级的量子查询下界？

（3）本文采用了一种简化的噪声模型，仅考虑了噪声强度的上界。更一般地，是否可以在更复杂的噪声假设下（例如，更贴近实际的量子噪声模型或随机噪声模型）从理论上分析非凸优化算法的鲁棒性与加速性，或通过数值模拟甚至在实际量子设备上进行验证？

[1]. Hualin Zhang, and Bin Gu. Faster gradient-free methods for escaping saddle points. The Eleventh International Conference on Learning Representations, 2022

[2]. Chi Jin, Praneeth Netrapalli, and Michael I. Jordan, Accelerated gradient descent escapes saddle points faster than gradient descent, Conference on Learning Theory, pp. 1042–1085, 2018

[3]. Chenyi Zhang and Tongyang Li, Escape saddle points by a simple gradient-descent based algorithm, Advances in Neural Information Processing Systems 34, 2021

[4]. Stephen P. Jordan, Fast quantum algorithm for numerical gradient estimation, Physical Review Letters 95, 2005

[5]. Shouvanik Chakrabarti, Andrew M. Childs, Tongyang Li, and Xiaodi Wu, Quantum algorithms and lower bounds for convex optimization, Quantum 4, 2020

[6]. Chenyi Zhang, Jiaqi Leng, and Tongyang Li, Quantum algorithms for escaping from saddle points, Quantum 5, 2021

[7]. Chi Jin, Praneeth Netrapalli, Rong Ge, Sham M. Kakade, and Michael I Jordan, On nonconvex optimization for machine learning: Gradients, stochasticity, and saddle points, Journal of the ACM (JACM) 68, 2021

[8]. Chi Jin, Lydia T. Liu, Rong Ge, and Michael I. Jordan, On the local minima of the empirical risk, Advances in Neural Information Processing Systems, vol. 31, 2018

[9]. John C. Duchi, Michael I. Jordan, Martin J. Wainwright, and Andre Wibisono, Optimal rates for zero-order convex optimization: The power of two function evaluations, IEEE Transactions on Information Theory 61, 2015

图文 | 张辰逸 龚维元

PKU QUARK Lab