Sci. Adv. | 机器学习赋能量子计算，自适应杂化泛函提高预测精度

今天为大家介绍的是来自加拿大多伦多大学O. Anatole von Lilienfeld团队的一篇论文。精确交换贡献（Exact exchange contributions）显著影响电子态，对共价键的形成和断裂产生影响。杂化密度泛函近似通过经验性平均精确交换混合已取得成功，但由于离域误差，其精度仍不及高级量子化学计算。作者提出了自适应杂化泛函（adaptive hybrid functionals），利用数据高效的量子机器学习模型实时生成最佳精确交换混合比例，且几乎不增加计算开销。自适应Perdew-Burke-Ernzerhof杂化密度泛函(aPBE0，作者提出的方法)在QM9、QM7b和GMTKN55基准数据集中改善了能量学、电子密度和HOMO-LUMO能隙。基于模型不确定性的约束使该方法在外推区域平滑地还原为PBE0，确保在有限训练下的普遍适用性。通过为不同自旋态调整精确交换分数，aPBE0有效解决了开壳层系统(如carbenes)中的自旋能隙问题。作者还提出了修订版QM9(revQM9)数据集，其中包含更准确的量子性质，包括更强的共价键合、更大的带隙、更局域化的电子密度以及更大的偶极矩。

加速新材料和化学品的逆向设计是实现更可持续未来的迫切需求。量子力学为我们提供了高保真度预测电子、光学和热学性质的能力，这对设计具有特定功能的材料至关重要。虽然原则上具有普适性，但由于巨大的计算复杂性，数值求解多体电子薛定谔方程对于除最简单系统外的所有系统仍然是一个突出的挑战。即使是最新和最有前景的基于机器学习(ML)的量子模型，仍然严重依赖大量训练数据，需要优化数百万个回归权重，并且难以在化学化合物空间中有效地进行外推。相比之下，密度泛函理论(DFT)是一种形式上精确的量子方法，但不幸的是，确切的密度泛函只是已知存在，没有找到它的具体方法。尽管如此，DFT使得定义和参数化密度泛函近似(DFAs)成为可能，这些近似在预测能力和计算成本之间提供了最可行的权衡——除了它们高度的可重现性——这有效地使DFT成为生物学、化学和材料科学中原子模拟的主要工具。DFT的这些特性也对化学和材料模拟中人工智能的快速增长至关重要，使得作者今天所见证的常规计算材料和分子发现活动能够获得巨大的加速。

多年来，人们对精确泛函做出了许多近似，虽然目前这是处理大量化合物类别和性质的最合理工具，但常见的密度泛函近似(DFAs)仍然难以达到其他后HF方法的精度。这些缺点中有很大一部分源于所谓的自相互作用误差，这种误差来自包含电子与自身相互作用的Hartree能量项。自相互作用，或一般的离域误差，表现在多个众所周知的方面，从带隙能量的不佳表现到自旋能隙的预测（对理解反应活性和磁性至关重要）都可能在定量和定性上出现错误。严格基于绝热连接，这些缺点中的一些可以通过使用杂化泛函来缓解，杂化泛函将Hartree-Fock(HF)交换（也称为精确交换）与DFA交换能量混合在一起（式1），其中a是混合参数，在0和1之间变化。最初为一般热化学参数化的全局杂化泛函包含固定数量的精确交换，通常在20%到25%左右。虽然传统杂化泛函如B3LYP或Perdew-Burke-Ernzerhof(PBE)0对能量学和电子密度的计算代表了重大进步，但它们并非万能：最近提出的DFAs为了改善能量预测而牺牲了电子密度计算的精度。

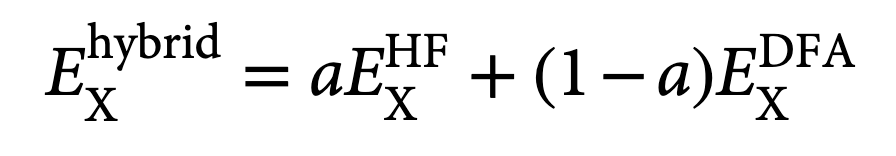
式1

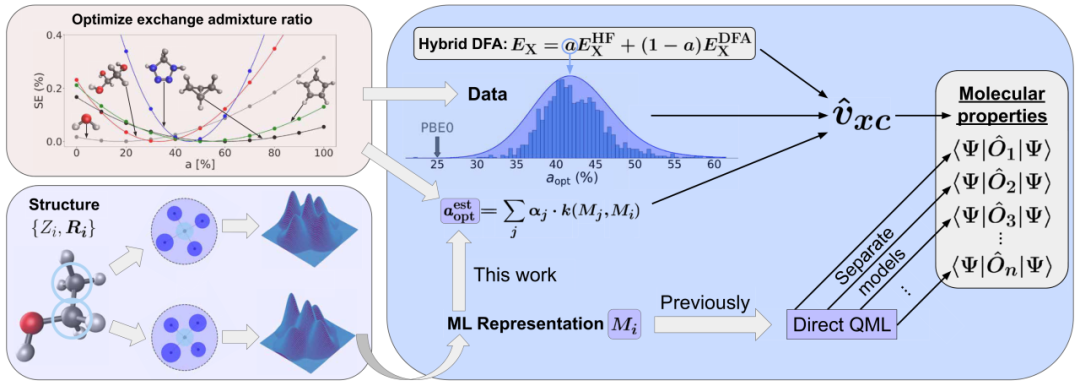
图 1

基于对先前研究的观察并利用绝热连接（adiabatic connection），作者假设最优HF/精确交换混合比例a_opt是一个系统特定的标量标签，它使得相对于可信的高级电子结构处理的DFA误差接近于零（见图1），并且具有足够的平滑特性以被机器学习建模。只要这个假设成立，作者指出，系统特定的最优混合比例不会违反能量守恒，因为它们只是再现任何能量守恒的参考理论水平。

下面，作者提供了大量支持这一假设的数值证据，并证明可以使用合适的机器学习模型（图1）在化学化合物空间中有效地回归和估计a_opt。基于最近引入的紧凑卷积多体分布泛函(cMBDF)表示，作者的基于核岭回归(KRR)的量子机器学习方案在数据效率上很高，并且在直接从定义电子系统的4N-6内部自由度映射到Kohn-Sham(KS)哈密顿量中仅在系统变化中轻微变化的一个标量参数方面很轻量。

作者选择KRR的主要原因是它在预测标量标签的低训练数据环境中表现出色（如已经在化学任务中证明的那样）。这与之前发布的旨在改进DFA的基于机器学习的努力有根本不同，后者更具挑战性，因为它们将完整的电子密度信息映射到在自洽场循环中变化的能量期望值，这些值是敏感且强烈变化的标签。

在下文中，作者展示了自适应HF混合比例的想法对各种性质都是有效的。为此，按照简约原则，作者选择了调整PBE0泛函，因为它基于非经验性广义梯度近似(GGA) PBE，而作者工作中使用的绝热连接的杂化DFA方案（式2）非常适合这一泛函。

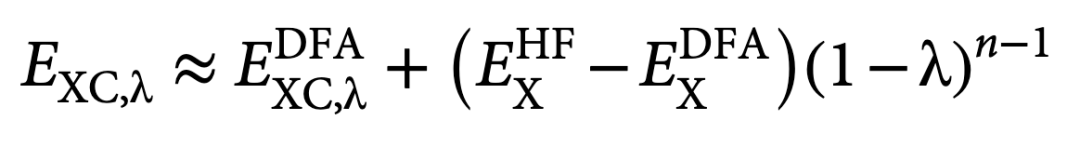
式 2

作者依靠量子机器学习模型实时预测这个单一参数，即在启动自洽场循环之前，仅使用核电荷和原子坐标作为输入，这有效地从通过绝热连接获得的泛函集合中为每个系统选择最优泛函。

由此产生的"自适应"PBE0(aPBE0)方法同时为原子化能(AEs)、前线轨道能隙/特征值和闭壳层分子的电子密度等性质提供了大幅改进的预测，这表明该方法没有牺牲一个可观测量的精度来提高另一个。

虽然假设这种最优泛函对每个外部势都存在，但该方法的普遍适用性需要一个训练充分的机器学习模型。为了解决这个问题，作者在该方法上设置了一个基于模型不确定性的约束，使其在远离训练区域的地方平滑地还原为PBE0泛函，促进了该方法向每个杂化泛函的安全扩展，并可能通过主动学习等方法持续改进。

这在标准GMTKN55基准测试中得到验证，在一些具有小预测不确定性的数据集上获得了显著改进，而大多数其余情况则还原为默认的PBE0结果。

自适应杂化泛函的性能评估

为评估自适应杂化泛函方法的潜力，作者首先讨论了aPBE0方法的可转移性和基础模型特性。作者首先研究了该方法对两个不同数据集和三个观测量的预测性能，即原子化能(AEs)、来自50个QM9分子的电子密度，以及在QM7b数据集中随机选择的100个有机分子的HOMO-LUMO能隙。对于本节中使用aPBE0呈现的所有结果，每个分子的a_opt值都由同一个机器学习模型预测，该模型在1169个a_opt值(仅使用AEs获得)上进行训练，这些值基于a_mon的饱和小型有机分子片段(为简洁起见，以下也称为分子片段)，这些片段来自QM5数据集且含有不超过五个重原子(参见材料与方法中的"优化"部分)。图1显示了训练集中1169个aopt值的相应分布，中心在约42%(另见材料与方法部分中的机器学习小节)。

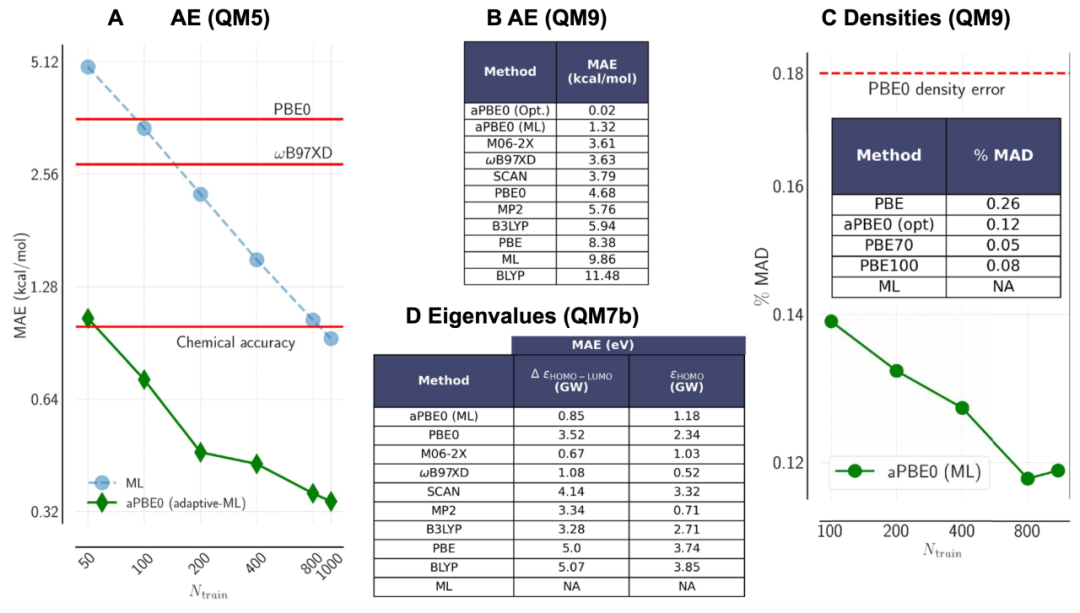
图 2

图2A显示了对QM5数据集中100个分子片段测试集的aopt值预测的学习曲线(ML模型预测误差随训练集大小的变化函数)。同一测试集上AEs的相应性能误差改进(通过使用预测的aopt值执行aPBE0计算获得)也在图2A中显示，表明在仅对50个分子进行a训练后就已达到化学精度(比默认PBE0低约3倍的误差)。这与直接学习曲线形成对比，直接学习曲线对应于直接预测AEs的ML模型(也显示在图2A中)，该模型需要近20倍的训练数据才能在相同的AEs测试集上达到化学精度。

使用在QM5的1169个分子片段上训练的相同模型进行预测，作者随后对73个研究中使用的50个大型QM9分子（每个含有九个重原子）执行了aPBE0计算。与PBE0相比，aPBE0原子化能的预测平均绝对误差（相对于CCSD(T)/cc-pVTZ）大幅降低，从PBE0的4.68 kcal/mol下降到1.32 kcal/mol（图2B）。与其他常见的密度泛函近似（DFAs）和MP2的比较表明，aPBE0方法大大优于最佳混合DFAs ωB97XD（3.63 kcal/mol）和M06-2X（3.61 kcal/mol）。在图2B中，作者还包括了使用此测试集中所有50个分子的真实最优HF交换比率得到的结果[aPBE0 (Opt.)]，这表明使用足够精确的aopt预测ML模型几乎可以获得精确的[CCSD(T)]原子化能。

虽然原子上的力几乎没有变化，但作者发现，获得的电子密度质量并没有因更准确的能量而牺牲，这与许多现代DFAs的情况不同。特别是，对于50个QM9分子，基于aPBE0的电子密度与相应CCSD估计的偏差也有所改善，从PBE0的0.18%下降到基于QM5训练集大小从100增加到1169时aPBE0的约0.12%（图2C）。绝对改进看起来不大，因为正如所指出的，PBE0密度本身就非常准确。aPBE0获得的密度相对于PBE0的相对改进接近33%。为进一步比较，图2C中还列出了基于PBE的混合泛函与HF交换值分别为0、25、70和100%的平均误差，这表明对于这些分子，电子密度的最优aopt值接近约70%的HF交换，比作者ML模型获得的平均aopt值更接近，而不是PBE0的25%值，因此导致了电子密度的观察到的改进。请注意，精确的泛函会同时为能量和密度提供精确的预测。因此，作者预计，如果在绝热连接（式2）的λ = 1相互作用极限使用比PBE更准确的基础DFA（例如SCAN），那么仅基于能量或仅基于密度的优化的aopt值会更接近。相比之下，请注意，试图直接学习和预测电子密度的传统监督ML模型即使在训练集大小增加到一个数量级后，也难以达到与参考值偏差小于1%的程度。

为评估前沿轨道特征值的同时变化，作者分析了从QM7b数据集中随机选择的100个有机分子的HOMO-LUMO特征值，以与该数据集中报告的参考GW基值进行比较。通常，有机分子片段的最优a值会增加（见图1），导致HOMO-LUMO能隙扩大，使预测更接近GW参考值。图2D量化了这一改进，与GW的偏差从PBE0的3.52 eV降低到aPBE0的0.86 eV，平均每分子改进2.67 eV（61.57 kcal/mol）（75.8%）。aPBE0方法优于所有常见的DFAs，除了M06-2X，后者平均仅比GW接近0.2 eV。需要注意的是，M06-2X是一种更昂贵的meta-GGA混合泛函，但它也可以被设计为自适应的。图2D还单独显示了HOMO特征值的误差，其中aPBE0提供了平均每分子1.16 eV（26.75 kcal/mol）的改进，相比PBE0，误差减少了49.6%。

通过DFT计算获得HOMO-LUMO能隙的更准确方法是计算电离势（IP）和电子亲和力（EA）之间的差异，这需要三次SCF计算。最优调谐（OT）混合泛函的方法也是一种自适应方法，旨在通过调整全局或范围分离混合泛函中的HF交换量或范围分离参数，准确获得HOMO-LUMO能隙。这些值与基于ωB97XD（OT-ωB97XD）泛函的OT混合进行了基准比较（详情见补充材料中的"键断裂"部分），当使用aPBE0代替PBE0时，作者也获得了0.22 eV的改进。

作者在此指出，这些改进以及电子密度的改进，来自仅通过优化原子化能获得的aopt值预测，即在损失函数中没有明确包含任何关于分子轨道（MO）特征值或电子密度的特定信息。此外，这种可转移性显得特别强健，因为所有呈现的预测不仅适用于不同的标签（原子化能、密度和能隙），还适用于来自不同于训练所用分布的分子（分别为QM9和QM7b分子用于预测，而训练使用QM5数据集中不超过五个重原子的饱和分子片段）。这必须与基于直接学习特定标签的ML方法形成对比。在图2A中，可以看到自适应ML方法aPBE0大大优于直接学习原子化能标签，因为aopt标签具有更小的方差，使其更适合ML。在图2B中更大分子的测试集上，两种方法之间的差异变得更大，这表明自适应ML [aPBE0 (ML)]方案也显示出比直接学习能量标签更大的可转移性。此外，对于其他观测量，即电子密度和MO特征值，直接和Δ ML基方案不适用，因为这些方法只能为它们被训练的标签（在本例中为原子化能）提供预测。这与基于自适应ML的aPBE0方案形成鲜明对比，后者由于嵌入到电子哈密顿量中，可以同时改进多个观测量，并突显了该方法的基础模型特性。作者进一步指出，两个ML模型都使用cMBDF表示，该表示被设计为有效学习分子能量，而不是aPBE0方法中使用的密集型aopt标签，因此，通过使用更适合aPBE0的表示/ML方法，训练数据效率可能会降低。

虽然QM9和QM7b数据集通常不旨在代表化学的一般性，但它们确实代表了可重现且相当规模的基准，表示化学相关领域的非平凡量子力学性质。然而，为了进一步分析aPBE0方法在有限训练条件下的一般适用性，作者转向标准GMTKN55基准测试，该测试涉及主族化学相关的基本性质、反应能量、能垒高度和非共价相互作用。为评估该方法的效率，作者仅在200个高质量的、使用W4复合方法获得的W4-17数据集中的完全构型相互作用、完全基组(FCI/CBS)估计的原子化能上进行了训练。再次，由于这些少量训练实例的可用性，数据高效的回归器如KRR对这项任务是最佳选择。该数据集比QM5覆盖了更多的化学元素，并允许作者处理无机物种。由于对ML模型施加的约束使其具有普遍适用性，它通过其不确定性估计，对远离其训练域的情况平滑地减少为PBE0(即预测25%的HF交换)。作者发现在模型不确定性高达70%的情况下有所改进，超过这一阈值，性能开始比默认PBE0下降。这一阈值的选择是该方法的一个超参数，可以根据可用的训练数据进行调整。

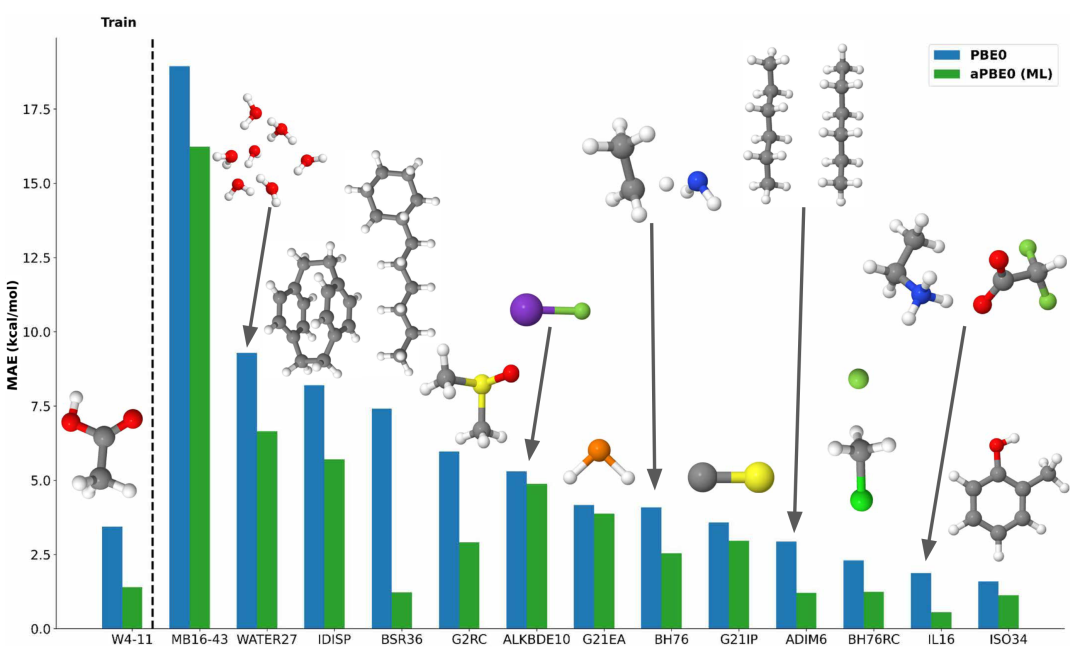
图 3

图3显示了GMTKN55基准测试中平均不确定性值低于70%阈值的13个子集的结果。对于WATER27数据集，去局域化误差是关键，困扰着所有在该数据集上显示较大误差的DFAs，而aPBE0减少了这些误差。BSR36数据集包含饱和烃的键分离反应，使用aPBE0方法由于改进了甲烷和乙烷的能量估计(它们几乎参与所有反应)而大大降低了反应误差。由于模型不确定性低，多个物种的能量估计得到改进，导致来自MB16-43、G2RC、BH76RC和ALKBDE10数据集的反应能量；来自BH76的能垒高度；来自G21IP和G21EA数据集的电离势和电子亲和力；来自ISO34数据集的有机分子异构化反应；以及在ADIM6、白细胞介素-16二聚体和IDISP反应中的非共价相互作用的预测更加准确。随着训练的增加，aPBE0可能在几乎所有热化学和动力学任务中获得实质性改进，正如Gould等人所注意到的，他们发现对GMTKN55中几乎所有反应都存在最优a_opt值。同时，基于预测不确定性的模型约束(如作者工作中使用的约束)应该与自适应混合方法一起使用，这保留了基础混合DFA的一般适用性和稳健性。

编译|黄海涛

审稿|王梓旭

Khan, D., Price, A. J., Huang, B., Ach, M. L., & von Lilienfeld, O. A. (2025). Adapting hybrid density functionals with machine learning. Science Advances, 11(5), eadt7769.