ICALP 2025 | 鲁棒聚类的核心集：基于黑箱规约至普通情形的构造方法

关键词：核心集聚类鲁棒性

导读

本文是 ICALP 2025 会议接收论文 Coresets for Robust Clustering via Black-box Reductions to Vanilla Case 的解读。该论文作者是北京大学计算机学院博士生楼家宁和北京大学计算机学院前沿计算研究中心助理教授姜少峰。

本研究针对鲁棒聚类问题，首次提出一种将问题黑盒规约至普通（非鲁棒）情形的核心集构造算法。该算法在理论上改进了核心集大小的上界，并能够应用于数据流算法等领域。

← 扫码跳转论文

论文地址：https://arxiv.org/abs/2502.07669

问题介绍

k

-Means 聚类问题是一个经典的组合优化问题，旨在寻找一个大小为

k

的点集作为聚类中心，以最小化所有数据点到聚类中心的距离平方和。现实数据集中常常包含噪声点，而

k

-Means 聚类的问题设定对这些噪声点非常敏感。例如，若在数据集中加入一个距离足够远的离群点（outlier）时，问题的最优解可能会错误地将该离群点作为聚类中心，从而导致聚类结果的偏差。

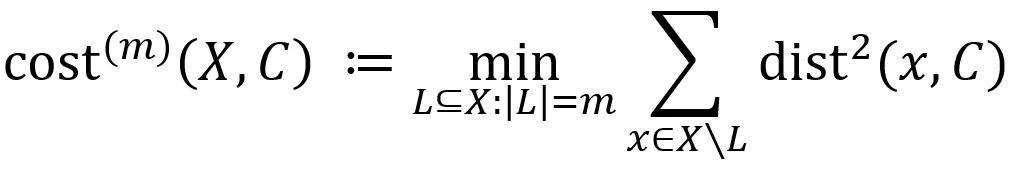
因此，本文聚焦于一种具有鲁棒性的 $k$ -Means 聚类变种：带有离群点的 $k$ -Means 聚类问题（k-Means with Outliers），记为 $(k,m)$ -Means，其中 $m$ 为指示离群点数量的参数。给定数据集 $X$ ， $(k,m)$ -Means 旨在找到一个大小为 $k$ 的聚类中心集 $C$ ，以最小化以下目标函数：

即，首先剔除最远的 $m$ 个点（视为离群点），然后在剩余点上应用 $k$ -Means 的目标函数。特别地，当 $m=0$ 时，该问题退化为普通的 $k$ -Means 聚类问题。

本文探索了“数据摘要”这一算法设计范式。我们针对带有离群点的聚类问题设计核心集（coresets）构造算法。核心集是一个极小的数据摘要，它保证对于任意聚类中心，在核心集上计算的目标函数值与在原数据集上计算的目标函数值之间的相对误差不超过某个容忍度 $\epsilon \gt 0$ 。核心集的大小通常远小于原数据集。因此，我们只需在核心集上运行现有的近似算法，即可获得原数据集的近似解，从而实现算法的加速。此外，核心集在亚线性算法设计中也具有广泛应用，包括数据流（streaming）算法、分布式（distributed）算法和动态（dynamic）算法等。

关于（非鲁棒） $k$ -Means 问题的核心集算法已有充分的研究。目前，最优的核心集算法能够构造大小为 $\tilde{O}(k\epsilon^{-4})$ 的核心集 [CLSS22]。然而，对于带有离群点的 $(k,m)$ -Means 聚类问题，目前最好的理论上界是 $\tilde{O}(m+k^2\epsilon^{-6})$ [HLLW25]。注意到，从 $m=0$ 的普通 $k$ -Means 问题到 $m=1$ 的仅含一个离群点的 $(k,1)$ -Means 聚类问题，核心集的大小发生了跳变，特别是 $k$ 的相关性从（几乎）线性变成至少平方级别。

技术上，目前鲁棒聚类的核心集（以下简称鲁棒核心集）都是通过对已有的普通聚类核心集（以下简称普通核心集）构造算法进行专门化改造。这种缺乏普适性的策略，是导致鲁棒核心集在技术与结果上均滞后于普通核心集的主要原因。例如，目前最优的鲁棒核心集算法是通过改造一个基于采样的普通核心集算法 [CSS21] 得到的，该算法构造出的核心集大小至少为 $\Omega(k^2)$ 。相比之下，当前最优的普通核心集算法已能通过更精细的采样方法构造出近乎线性于 $k$ 的 $\tilde{O}(k\epsilon^{-4})$ 大小的核心集 [CLSS22]。如何将这类精细采样策略推广应用于鲁棒核心集的构造，仍是一个具有挑战性的开放问题。

主要结果

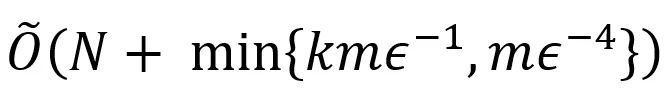
本文旨在系统地探索鲁棒核心集与普通核心集之间的关系，首次提出了一种基于黑盒规约的核心集构造算法。具体来说，假设存在一个针对 $k$ -Means 的算法，能构造大小为 $N$ 的普通核心集。那么，文章证明存在一个针对鲁棒 $(k,m)$ -Means 的算法，能构造大小为

的鲁棒核心集。该算法首次实现了从 $m=0$ （普通聚类情形）到 $m=1$ （带有一个离群点情形）的平滑过渡。当代入 $N=\tilde{O}(k\epsilon^{-4})$ ，即目前普通核心集的最优上界时，我们得到大小为 $\tilde{O}((k+m)\epsilon^{-4})$ 的鲁棒核心集，在参数 $k$ 和 $\epsilon$ 的指数上改进了先前的 $\tilde{O}(m+k^2\epsilon^{-6})$ ，并且首次实现了关于参数 $k$ 的（几乎）线性依赖性。

得益于“黑盒规约”的特性，该算法成为首个具有普适性的鲁棒核心集构造方法 —— 若普通核心集的大小 $N$ 得到进一步优化，该方法可直接导出相应的鲁棒核心集改进结果。此外，该算法同样适用于多种不同的场景和设定，包括：

确定性构造算法：由于存在一个确定性算法能够构造大小为 $\text{poly}(k\epsilon^{-1})$ 的普通核心集 [CSS23]，我们可以得到一个性能相似的鲁棒核心集的确定性构造算法。
低维欧氏空间：在低维欧氏空间中，针对 $1$ -Means 这一特殊情况，存在大小为 $\tilde{O}(\sqrt{d} \cdot \epsilon^{-1})$ 的核心集 [HHHW23]。因此，我们可以得到大小为 $\tilde{O}((m+\sqrt{d})\cdot \epsilon^{-1})$ 的鲁棒 $(1,m)$ -Means 聚类核心集。
动态数据流算法：动态数据流模型考虑数据集以包括数据点插入和删除的数据流形式给出，要求用尽可能小的内存来计算核心集。在假设数据集来自离散空间 $[\Delta]^d$ 的情况下，通过规约至已有的空间复杂度为 $\tilde{O}(k)\cdot\text{poly}(\epsilon^{-1}d\log \Delta)$ 的普通 $k$ -Means 核心集算法 [HSYZ18]，我们可以得到空间复杂度为 $\tilde{O}(k+m)\cdot\text{poly}(\epsilon^{-1}d\log \Delta)$ 的鲁棒 $(k,m)$ -Means 核心集算法。这也是首个针对动态数据流的鲁棒聚类核心集算法。

主要技术总结

本文提出了两个条件，满足任意一个条件时，普通核心集也自动成为鲁棒核心集。

第一个条件要求数据集是“稠密的”。即，对于任意一个数据点，在其一定距离的领域内，至少存在 $\Omega(m\epsilon^{-1})$ 个数据点。直观上，这意味着数据集中不存在离群点，因此，针对该数据集的任意普通核心集也同样是鲁棒核心集。根据这一条件，本文提供了一种新的数据集分解方法，将数据集分为稠密部分和少量的 $O(km\epsilon^{-1})$ 个稀疏点，从而得到第一种大小为 $N+O(km\epsilon^{-1})$ 的鲁棒核心集构造算法（其中 $N$ 是普通核心集的大小）。

第二个条件要求核心集额外满足一个 “size-preserving” 的性质。粗略地说，存在一种将数据集分解为小直径部分的方式，使得核心集在每个部分上具有相同数量（或相同比例）的点。基于这一条件，本文利用了一种称为稀疏划分（sparse partition）[JLN+05] 的数据划分方法，对数据集进行预处理，使得在预处理后的数据集上构造的普通核心集能够（近似）满足“size-preserving”的要求，从而进一步得到鲁棒核心集。结合第一个条件的算法，我们能够得到第二种大小为 $\tilde{O}(N+m\epsilon^{-4})$ 的核心集构造算法。该算法避免了参数 $k$ 与 $m$ 的相乘。

参考文献

[CLSS22] Vincent Cohen-Addad, Kasper Green Larsen, David Saulpic, and Chris Schwiegelshohn. Towards optimal lower bounds for k-median and k-means coresets. In STOC, pages 1038–1051. ACM, 2022.

[CSS21] Vincent Cohen-Addad, David Saulpic, and Chris Schwiegelshohn. A new coreset framework for clustering. In STOC, pages 169–182. ACM, 2021.

[CSS23] Vincent Cohen-Addad, David Saulpic, and Chris Schwiegelshohn. Deterministic clustering in high dimensional spaces: Sketches and approximation. In FOCS, pages 1105–1130. IEEE, 2023.

[HHHW23] Lingxiao Huang, Ruiyuan Huang, Zengfeng Huang, and Xuan Wu. On coresets for clustering in small dimensional euclidean spaces. In ICML, volume 202 of Proceedings of Machine Learning Research, pages 13891–13915. PMLR, 2023.

[HLLW25] Lingxiao Huang, Jian Li, Pinyan Lu, and Xuan Wu. Coresets for constrained clustering: General assignment constraints and improved size bounds. In SODA, pages 4732–4782. SIAM, 2025.

[HSYZ18] Wei Hu, Zhao Song, Lin F. Yang, and Peilin Zhong. Nearly optimal dynamic k-means clustering for high-dimensional data. CoRR, abs/1802.00459, 2018.

[JLN+05] Lujun Jia, Guolong Lin, Guevara Noubir, Rajmohan Rajaraman, and Ravi Sundaram. Universal approximations for tsp, steiner tree, and set cover. In STOC, pages 386–395. ACM, 2005.

图文 | 楼家宁

PKU 姜少峰Lab

姜少峰博士，现任北京大学前沿计算研究中心助理教授、北京大学博雅青年学者，于2021年正式加入中心。他于2017年在香港大学获得博士学位，曾在以色列魏茨曼科学研究学院进行博士后研究，并曾在芬兰阿尔托大学任助理教授。他的研究方向为理论计算机科学，近期侧重于大数据算法及其在机器学习中的应用，并已在包括 STOC，FOCS，SICOMP，SODA，ICML，NeurIPS 等主流国际期刊和会议上发表论文多篇。

姜少峰Lab相关科研动态

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点“阅读原文”转论文链接

内容中包含的图片若涉及版权问题，请及时与我们联系删除

ICALP 2025 | 鲁棒聚类的核心集：基于黑箱规约至普通情形的构造方法

评论