ICALP 2025 | k-Center问题——基于大规模并行计算下的完全可扩展算法

关键词：大规模并行计算; 欧氏空间; k-Center

导读

本文是对已被 ICALP 2025 接收的 Fully Scalable MPC Algorithms for Euclidean k-Center 一文的解读。该工作由北京大学姜少峰课题组与 University of Warwick 的 Artur Czumaj、MIT 的 Mohsen Ghaffari 合作完成，论文主要贡献者之一高贵晨为北京大学计算机学院博士生。

论文聚焦于大规模并行计算（Massively Parallel Computation, MPC）模型下欧氏空间中 k-Center 问题，分别在低维和高维的设定下设计了完全可扩展的常数轮 MPC 算法。

← 扫码跳转论文

论文地址：https://arxiv.org/abs/2504.16382

问题及背景

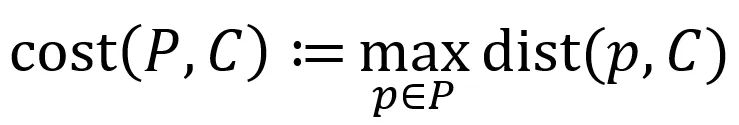
对大规模数据进行聚类是计算机科学中一项基本的计算任务，我们考虑欧氏空间下的 $k$ -Center 问题。给定一个包含 $n$ 个数据点的集合 $P\subset \mathbb{R}^d$ ，一个整数 $k\ge1$ ， $k$ -Center 问题是要找到一个大小至多为 $k$ 的数据集合 $C\subset \mathbb{R}^d$ ，使得所有 $P$ 中的数据点到集合 $C$ 中最近点的最大距离最小，即找到 $C\subset\mathbb{R}^d$ 并最小化

其中， $\text{dist}(p,C)=\min_{c\in C} \parallel p-c\parallel_2$ 表示 $p$ 点到 $C$ 中最近点的欧氏距离。

MPC 模型最早由 Karloff、Suri 和 Vassilvitskii^[1]于2010年提出，是并行计算中一种重要的模型，可以用来建模 Hadoop、Spark 等众多实际广泛应用的并行计算框架。在 MPC 模型中，设有 $m$ 台机器，每台机器都有大小为 $s$ 的内存。典型情况下，假定内存为 $s=n^\alpha$ 且常数 $\alpha\in(0,1)$ ，其中 $n$ 是输入数据量的大小。此外，计算以同步轮进行，在每一轮中，任何一台机器都可以向/从任何其他机器发送/接收信息，前提是从/向每台机器传输的数据总量为 $O(s)$ 。MPC 算法的效率是通过轮数来衡量的，并且一般追求常数轮的算法。

除了轮数尽量追求常数轮，MPC 算法还应该是完全可扩展（Fully Scalable）的：即算法在任何内存参数 $s=n^\sigma,\sigma\in(0,1)$ 下都可以运行，尤其是对于 $k$ -Center 而言，需要满足 $s$ 与 $k$ 无关。目前针对 $k$ -Center 问题的完全可扩展的工作较少^{[2, 3]}，且仅限于低维欧氏空间下的结果。当前最好结果仅是 $O(\log\log n)$ 轮的 $(O(\log^* n),1+o(1))$ -双标准近似^[3]，其中 $(\alpha,\beta)$ -双标准近似是指算法输出至多 $\beta k$ 个中心点，且其代价至多是 $k$ 个中心点的最优代价的 $\alpha$ 倍。因此，为 $k$ -Center 问题在低维和高维欧式空间下设计完全可扩展、常数轮、常数近似的 MPC 算法是该领域的挑战之一。

主要结果

针对欧氏空间（包括低维和高维）中的 $k$ -Center 问题，我们都得到了完全可扩展的常数轮 MPC 算法。在低维欧式空间中，我们设计了第一个常数轮、常数近似（ $(2+\varepsilon)$ -近似）的完全可扩展 MPC 算法。该结果在多个关键方面（包括通信轮数、近似比等）显著优于现有的低维 $k$ -Center 完全可扩展 MPC 算法^{[2, 3]}。进一步地，如果允许双标准近似，我们可以改进 $(2+\varepsilon)$ -近似：我们设计了一个 $(1+\varepsilon)$ -近似的算法，该算法仅使用 $(1+\varepsilon)k$ 个中心点。在高维欧式空间中，我们提出了首个常数轮、 $O(\varepsilon^{-1}\log n/\log\log n)$ -近似的完全可扩展 MPC 算法。

技术概述

我们针对 $k$ -Center 问题所设计的算法，基于将其规约为几何版本的 Ruling Set（RS）和  Minimum Dominating Set（MDS）问题，而这两类问题是分布式计算中的基本问题。下面，我们将给出 RS 和 MDS 的定义、规约和结果，并重点概述高维 RS 的重要组成部分以及技术思想。

几何RS和MDS的规约和结果

\tau,\alpha,\varepsilon\gt0

是参数，OPT 表示

k

-Center 问题的最优解的值。

几何 RS 和 MDS 的定义：对于集合 $P$ 的子集 $S\subseteq P$ ，若对任意 $x\ne y\in S$ ，有 $\text{dist}(x,y)\gt\tau$ ，则称 $S$ 为 $P$ 的 $\tau$ -独立集（τ-IS）。对于集合 $S\subseteq \mathbb{R}^d$ ，若对任意 $x\in P$ ，有 $\text{dist}(x,S)\le \tau$ ，则称 $S$ 为 $P$ 的 $\tau$ -支配集（τ-DS）。若 $S\subseteq P$ 同时是集合 $P$ 的 $\tau$ -IS和 $\alpha$ -DS，则称其为集合 $P$ 的 $(\tau,\alpha)$ -Ruling Set（(τ,α)-RS）。一个 $\tau$ -MDS 集合是具有最少数据点的 $\tau$ -DS，记为 $\text{MDS}_\tau(P)$ 。一个相关的经典概念是极大独立集（MIS），其中 $\tau$ -MIS 是一种 $(\tau,\tau)$ -RS。

规约：已有研究表明（参见例如^[4]），若 $\tau\ge2\text{OPT}$ ，则集合 $P$ 的任何一个 $\tau$ -IS至多包含 $k$ 个数据点。因此，一个能计算 $P$ 的 $(2\text{OPT},\alpha)$ -RS 的 MPC 算法，将产生数据集 $P$ 上 $k$ -Center 问题的 $\alpha$ -近似。另一方面，对于 MDS，若令 $\tau=\text{OPT}$ ，由于 $k$ -Center 的最优解自身就是一个 $\tau$ -MDS 的候选解，其大小最多为 $k$ ，所以对 $\tau$ -MDS 的 $(1+\varepsilon)$ -近似将得到 $(1+\varepsilon)k$ 个中心点。这种关系有助于获得 $k$ -Center 问题的双标准近似解。相比之下，RS 的设定要求解必须从数据集 $P$ 中选取，因此仅能得到 $O(1)$ 近似；而 MDS 则可以在整个 $\mathbb{R}^d$ 上操作，这一点对于获得 $(1+\varepsilon)$ -近似尤其关键，因为中心点必须从 $\mathbb{R}^d$ 中选择，而不仅限于数据集 $P$ 。

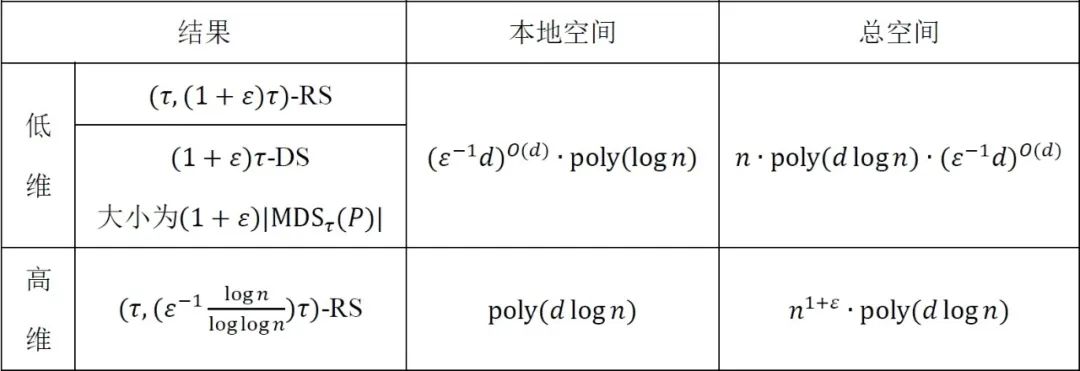
RS 和 MDS 的结果：我们在低维和高维设定下分别获得了关于 RS 和 MDS 的结果，如表1所示。结合前文所述的规约方法，这些结果自然地推出了 $k$ -Center 在低维和高维中的结果。所有结果均可在 $O(\log_sn)$ 轮内得到，这在典型设定 $s=n^\sigma$ 下是常数轮的，其中 $\sigma\in(0,1)$ 为常数。

表1. RS 和 MDS 的结果，所有结果均可在 $O(\log_sn)$ 轮内得到

MIS、RS 和 MDS 是 MPC 中基础却非常具有挑战性的问题。已有的相关研究大多集中在（一般）图或一般度量空间上，并且这些研究所取得的界限往往不如我们的结果，例如，他们需要使用超常数轮数的算法^[5-10]，和/或不是完全可扩展的^{[9, 11, 12]}。我们的结果似乎表明，这些问题在欧式空间中的表现与在图/一般度量空间中的表现非常不同。一方面，我们在低维和高维下都得到了完全可扩展的算法；但另一方面，我们的算法对于 MIS 和 MDS 来说仍然只是“近似解”，例如，在低维情况下，我们的 RS 和 MDS 结果对 MIS 和 MDS 的支配参数都有 $(1+\varepsilon)$ 的偏差。对于不违反支配参数的 RS/MIS 和 MDS，我们目前只知道一类关于增长有界图（growth-bounded graphs）的分布式计算研究（参见 Schneider 和 Wattenhofer 的工作^[13]），其间接地实现了 $O(\log^*n)$ 轮的完全可扩展算法，用于低维欧式空间的 MIS/MDS 问题。目前仍未有在常数轮内解决 MIS 问题的完全可扩展算法，即使是在二维空间中也是如此。实际上，即使是在输入集合直径为 $O(\tau)$ 的二维空间中，该问题也是具有挑战性的。尽管如此，我们的 RS 和 MDS 的结果已经足够用于 $k$ -Center 问题的近似求解。

高维设定下的 RS

我们在高维空间中提出的 $(\tau,O(\log n/\log\log n)\tau)$ -RS 是对著名的 Luby 算法的改造。第一个改造点在于，与经典的 Luby 算法^[14]需要运行 $O(\log n)$ 次迭代不同，我们的算法仅运行一次迭代的 Luby 算法：对于每个数据点 $x\in P$ ，生成一个均匀随机值 $h(x)\in [0,1]$ ，然后对于每个 $x\in P$ ，如果 $x$ 在球体 $B_P(x,\tau)$ （其中 $B_p(x,\tau)$ 代表数据集 $P$ 与以 $x$ 为中心、 $\tau$ 为半径的球的交集）中具有最小的 $h$ 值，则将其加入 RS 集合。该一次迭代的 Luby 算法能够以高概率产生 $(\tau,O(\log n)\tau)$ -RS。不过该结果仍比我们可以得到的 $(\tau,O(\log n/\log \log n)\tau)$ -RS 要差，并且上述一次迭代的 Luby 算法也未必可以直接用于欧氏空间。

基于几何哈希的预处理步骤：为了突破 $O(\log n)$ ，我们需要在一次迭代 Luby 算法之前引入第二项重要的改造：一个基于几何哈希的预处理步骤。几何哈希通过将 $\mathbb{R}^d$ 中的数据点映射到离散的哈希桶中（即对空间进行划分），使得哈希值相同的点被分配到同一个桶。具体而言，在执行一次迭代的 Luby 算法之前，我们先对所有数据点应用几何哈希，将其分配到对应的桶中。我们使用的是一致哈希^[15]，其中每个桶的直径为 $\ell:=O(\log n / \log \log n) \tau$ ，并且对于任意一个直径至多为 $O(\tau)$ 的子集合 $S\subseteq\mathbb{R}^d$ ，与 $S$ 相交的桶的数量最多为 $\Lambda:=\text{poly}(\log n)$ 。我们从每个非空桶中任选一个点组成集合 $P'$ ，在该集合上运行一次迭代的 Luby 算法。显然，该哈希步骤仅会使支配参数最多增加 $\ell=O(\log n/\log \log n)\tau$ ，这是我们可以接受的量级。这种舍入（分桶）的主要目的是为了限制每个点的 $O(\tau)$ -邻域的大小，这与图中点的度数是类似的。

总结

本文探索了低维和高维欧式空间中 $k$ -Center 问题的完全可扩展的 MPC 算法。对于高维欧氏空间，尽管本文的研究给出了 $O(\log n/\log\log n)$ -近似的 $k$ -Center，但是否存在完全可扩展的、常数近似的 $k$ -Center 依然是一个公开问题。

参考文献

[1] Howard J. Karloff, Siddharth Suri, and Sergei Vassilvitskii. A model of computation for MapReduce. SODA 2010.

[2] MohammadHossein Bateni, Hossein Esfandiari, Manuela Fischer, and Vahab S. Mirrokni. Extreme k-center clustering. AAAI 2021.

[3] Sam Coy, Artur Czumaj, and Gopinath Mishra. On parallel k-center clustering. SPAA 2023.

[4] Dorit S. Hochbaum and David B. Shmoys. A unified approach to approximation algorithms for bottleneck problems. Journal of the ACM 1986.

[5] Krzysztof Onak. Round compression for parallel graph algorithms in strongly sublinear space. arXiv 2018.

[6] Mohsen Ghaffari and Jara Uitto. Sparsifying distributed algorithms with ramifications in massively parallel computation and centralized local computation. SODA 2019.

[7] Mohsen Ghaffari, Christoph Grunau, and Ce Jin. Improved MPC algorithms for MIS, matching, and coloring on trees and beyond. DISC 2020.

[8] Chetan Gupta, Rustam Latypov, Yannic Maus, Shreyas Pai, Simo Särkkä, Jan Studený, Jukka Suomela, Jara Uitto, and Hossein Vahidi. Fast dynamic programming in trees in the MPC model. SPAA 2023.

[9] Jeff Giliberti and Zahra Parsaeian. Massively parallel ruling set made deterministic. DISC 2024.

[10] Hongyan Ji, Kishore Kothapalli, Sriram V. Pemmaraju, and Ajitanshu Singh. Fast deterministic massively parallel ruling sets algorithms. ICDCN 2025.

[11] Mélanie Cambus, Fabian Kuhn, Shreyas Pai, and Jara Uitto. Time and space optimal massively parallel algorithm for the 2-ruling set problem. DISC 2023.

[12] Alireza Haqi and Hamid Zarrabi-Zadeh. Almost optimal massively parallel algorithms for k-center clustering and diversity maximization. SPAA 2023.

[13] Johannes Schneider and Roger Wattenhofer. An optimal maximal independent set algorithm for bounded-independence graphs. Distributed Computing 2010.

[14] Michael Luby. A simple parallel algorithm for the maximal independent set problem. STOC 1985.

[15] Artur Czumaj, Arnold Filtser, Shaofeng H.-C. Jiang, Robert Krauthgamer, Pavel Veselý, and Mingwei Yang. Streaming facility location in high dimension via geometric hashing. FOCS 2022.

图文 | 高贵晨

PKU 姜少峰Lab

姜少峰博士，现任北京大学前沿计算研究中心助理教授、北京大学博雅青年学者，于2021年正式加入中心。他于2017年在香港大学获得博士学位，曾在以色列魏茨曼科学研究学院进行博士后研究，并曾在芬兰阿尔托大学任助理教授。他的研究方向为理论计算机科学，近期侧重于大数据算法及其在机器学习中的应用，并已在包括 STOC，FOCS，SICOMP，SODA，ICML，NeurIPS 等主流国际期刊和会议上发表论文多篇。

姜少峰Lab相关科研动态

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

点“阅读原文”转论文链接

内容中包含的图片若涉及版权问题，请及时与我们联系删除

ICALP 2025 | k-Center问题——基于大规模并行计算下的完全可扩展算法

评论