
Stanford CS224W: Machine Learning with Graphs
By Paul Aurel Diederichs and Anya Fries as part of the Stanford CS 224W Final Project
https://colab.research.google.com/drive/1Uds5r4QWcB5bsELiyBM8TBHEHFVCVcd3?usp=sharing
A learned solution to node-level classification on irregular graphs via graph neural networks.
基于图神经网络的不规则图节点级分类的解决方案
Deep learning has shown tremendous success on 2D visual recognition tasks. Tasks such as image classification and segmentation, deemed extremely difficult a decade ago, are now solved by neural networks with human-like performance. This success is attributed to convolutional neural networks (CNNs), which have replaced handcrafted descriptors. Driven by the success of CNNs on 2D images, researchers have extended CNNs to irregular graph data, such as 3D meshes. The extension of the convolutional operation to unstructured graph data is nontrivial as the notion of relative position is lost. Therefore, we have dedicated this blog post and a Colab to answering how CNNs can be generalized to irregular graphs. In particular, we discuss how to modify CNNs to predict segmentation masks on 3D meshes.
深度学习在 2D 视觉识别任务中取得了巨大的成功。图像分类和分割等被认为十年前极其困难的任务,现在已被具有类人性能的神经网络所解决。这种成功归因于卷积神经网络(CNN),它取代了手工制作的描述符。在 CNN 在 2D 图像上取得成功后,研究人员将 CNN 扩展到了非规则图数据,例如 3D 网格。将卷积操作扩展到非结构化图数据是非平凡的,因为相对位置的概念丢失了。因此,我们专门撰写了这篇博客文章和一个 Colab,以回答如何将 CNN 推广到非规则图。特别是,我们讨论了如何修改 CNN 以在 3D 网格上预测分割掩码。
Why are CNNs not applicable?
为什么卷积神经网络不适用?
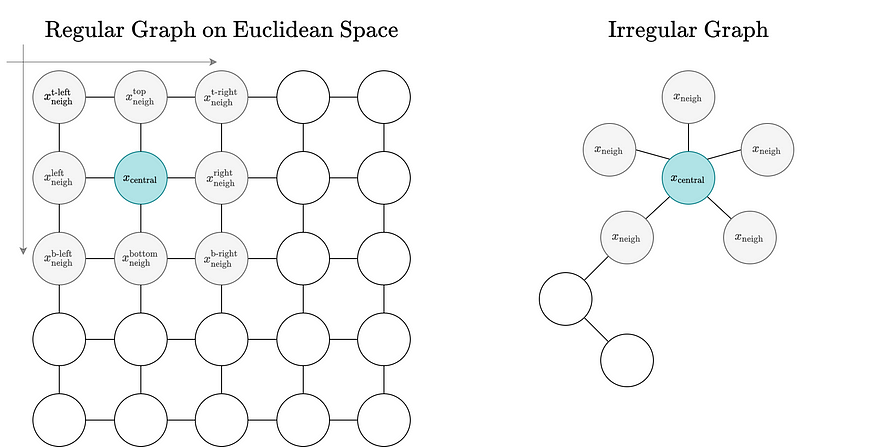
Regular graphs defined on the euclidean have a fixed node ordering and neighborhood size. Generic graphs have no node ordering for neighbors, and their number of neighbors is variable.
定义在欧几里得空间上的规则图具有固定的节点顺序和邻域大小。通用图没有邻居的节点顺序,并且它们的邻居数量是可变的。
Unfortunately, CNNs do not directly translate to irregular graphs. CNNs work in Euclidean space and on regular graphs, where neighboring nodes can be differentiated from one another via their relative position to the central node, and the number of neighboring nodes is constant. The convolutional operation leverages both of these properties to derive informative node embeddings. For irregular and unstructured graphs, these properties are not satisfied. Unstructured graphs have no notion of relative position — there is no top, bottom, right, or left. Additionally, the neighborhood connectivity/size can vary across nodes. Consequently, it is impossible to perform convolutional operations on irregular graphs.
不幸的是,卷积神经网络(CNN)并不能直接应用于非规则图。CNN 在欧几里得空间和规则图上工作,其中节点的相邻关系可以通过它们相对于中心节点的相对位置来区分,并且每个节点的相邻节点数量是恒定的。卷积操作利用了这两种属性来推导出信息丰富的节点嵌入。对于非规则和非结构化的图,这些属性并不满足。非结构化图没有相对位置的概念——没有顶部、底部、右侧或左侧。此外,节点的邻域连接性/大小可以跨节点变化。因此,在非规则图上无法执行卷积操作。
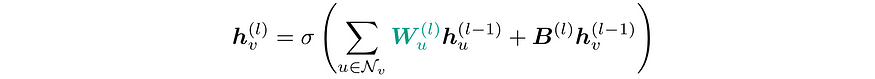
Update formula for computing node embeddings h with a 3x3 CNN layer. Note that unique weight matrices W are learned for each neighbor. This is possible because neighbors can be differentiated using their relative position to the center node.
用于计算节点嵌入 h 的 3x3 CNN 层的更新公式。注意,每个邻居都有唯一的权重矩阵 W。这是可能的,因为可以通过邻居相对于中心节点的相对位置来区分它们。
Graph Convolution Networks
图卷积网络
Since vanilla convolutional operations do not apply to irregular graphs, the operation needs to be re-formulated. Graph convolution networks (GCNs) and graph convolution operations are such a re-formulation. Similar to traditional CNNs, GCNs reason over the local neighborhood. Like CNNs, GCNs compute embeddings by aggregating information from direct neighbors. Yet, GCNs ensure that this information aggregation operation does not depend on the node’s relative position, nor on the node ordering, and is independent of the node’s neighborhood size — invariances not enforced by CNNs.
由于普通的卷积操作不适用于非规则图,因此需要对操作进行重新表述。图卷积网络(GCNs)和图卷积操作就是这样一种重新表述。类似于传统的 CNN,GCN 在局部邻域中进行推理。像 CNN 一样,GCN 通过聚合来自直接邻居的信息来计算嵌入。然而,GCN 确保这种信息聚合操作不依赖于节点的相对位置,也不依赖于节点的顺序,并且与节点的邻域大小无关——这是 CNN 没有强制执行的等变性。
Irregular graphs are node order invariant, so the output of a GCN must be independent of the graph’s node ordering. Specifically, the neural network’s output must be identical irrespective of the node ordering. We do not want the neural network to output two different values if fed two different node orderings of a graph. This property is known as permutation invariance. We illustrate it below.
非规则图是节点顺序不变的,因此 GCN 的输出必须与图的节点顺序无关。具体来说,神经网络的输出必须与节点顺序无关。我们不想让神经网络在输入图的两种不同节点顺序时输出两个不同的值。这种特性被称为置换不变性。我们下面进行说明。
The connectivity of nodes can differ across the graph. Thus, the graph convolution operation must be independent of the neighborhood size.
节点的连接性可能在不同图中有所不同。因此,图卷积操作必须与邻域大小无关。
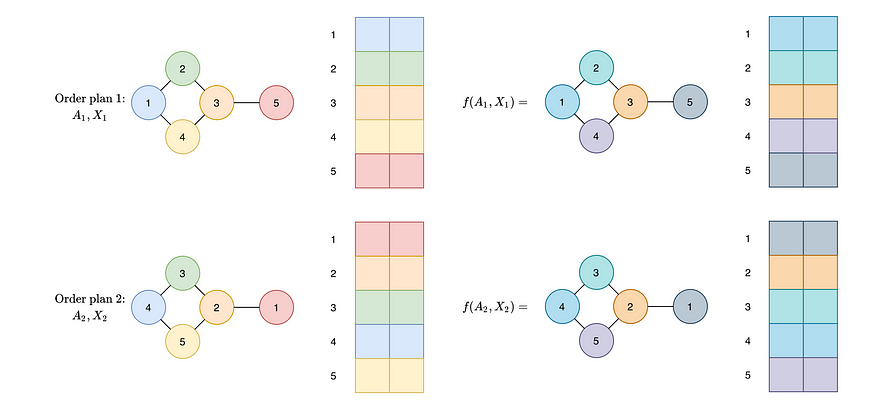
For different order plans, the learned function must map nodes to the same output irrespective of their order (permutation equivariance — illustrated), and must map graphs to the same vector (permutation invariance) irrespective of the graph’s node ordering.
对于不同的排序计划,学习到的函数必须将节点映射到相同的输出,无论它们的顺序如何(置换等变性——如图所示),并且必须将图映射到相同的向量(置换不变性),无论图的节点顺序如何。
A single GCN layer is defined by three operations: the message computation, the aggregation, and the update. These operations are performed to derive node embeddings.
单个 GCN 层由三个操作定义:消息计算、聚合和更新。这些操作用于推导节点嵌入。
Message computation: Message computation amounts to transforming the feature vector of each node in the graph. The applied learned transformation is common to all nodes to enforce permutation invariance.
消息计算:消息计算相当于对图中每个节点的特征向量进行转换。所应用的学习到的转换对所有节点都是通用的,以强制置换不变性。
Aggregation: Once all messages are derived, each node aggregates messages of its neighbors via a permutation equivariant function, e.g. mean, max, or sum function. This aggregation of messages enables the propagation of information across the graph.
聚合:一旦所有消息都派生出来,每个节点通过一个置换等变函数(例如均值、最大值或求和函数)聚合其邻居的消息。这种消息的聚合使得信息能够在图中传播。
Update: Finally, an update function combines the aggregated messages and the previous node embedding of the current node. Thereby the node’s embedding is updated. By combining information from the node’s neighborhood and the node itself, the derived node descriptor encodes structural and node-level information.
更新:最后,更新函数结合了聚合的消息和当前节点的先前嵌入。从而更新节点的嵌入。通过结合来自节点邻域和节点本身的信息,推导出的节点描述符编码了结构和节点级信息。
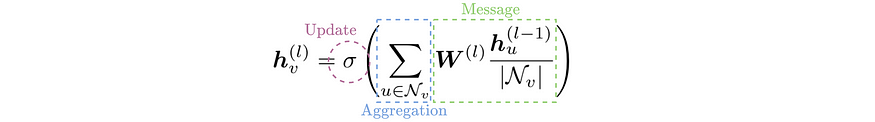
General message, aggregation and update formula for a GCN with node embeddings h. Messages are normalised by the node degree, the aggregation is a sum over the neighbors & the current node, and an activation is applied to update the embedding. Note that W does not depend on the current node or its neighbors.
一般消息,图卷积网络(GCN)的节点嵌入 h 的聚合和更新公式。消息由节点度数归一化,聚合是邻居和当前节点的和,并且应用激活函数来更新嵌入。请注意,W 不依赖于当前节点或其邻居。
For a more detailed explanation, have a look at lectures 6 and 7 of Stanford’s course on ML with graphs — CS224W.
想要更详细的解释,可以查看斯坦福大学机器学习与图课程的第 6 和第 7 次讲座——CS224W。
http://web.stanford.edu/class/cs224w/index.html#schedule
应用
To explore the introduced graph convolution operation, we turn to a graph segmentation task. Similar to image segmentation, where pixels are assigned to semantic classes, graph segmentation amounts to finding a mapping between the nodes of a graph and a set of classes. We focus on the problem of assigning body-part labels to the nodes of humanoid 3D meshes.
为了探索引入的图卷积操作,我们转向图分割任务。类似于图像分割,其中像素被分配到语义类别,图分割意味着在图的节点和一组类别之间找到一个映射。我们专注于将身体部位标签分配给类人 3D 网格的节点的问题。
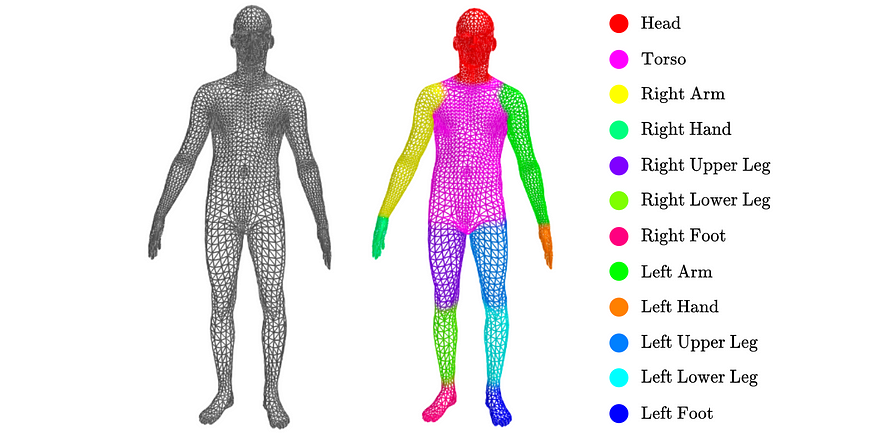
Graph segmentation task: each vertex in the mesh is assigned to one of twelve body-parts.
图像分割任务:网格中的每个顶点被分配到十二个身体部位之一。
3D Mesh Data 三维网格数据
To solve the presented segmentation task, we leverage all data encoded in 3D meshes. A 3D mesh defines a surface via a collection of vertices and triangular faces. It is represented by two matrices:
为了解决提出的分割任务,我们利用了 3D 网格中编码的所有数据。3D 网格通过顶点和三角面集合定义一个表面。它由两个矩阵表示:
A vertex matrix with dimensions (n, 3), where each row specifies the spatial position, [x, y, z] of a vertex in 3D-space.
顶点矩阵,维度为(n, 3),其中每一行指定 3D 空间中一个顶点的空间位置[x, y, z]。
A face integer matrix with dimensions (m, 3), where each row holds three indices of the vertex matrix that define a triangular face.
面整数矩阵,维度为(m, 3),其中每一行包含三个顶点矩阵的索引,这些索引定义了一个三角面。
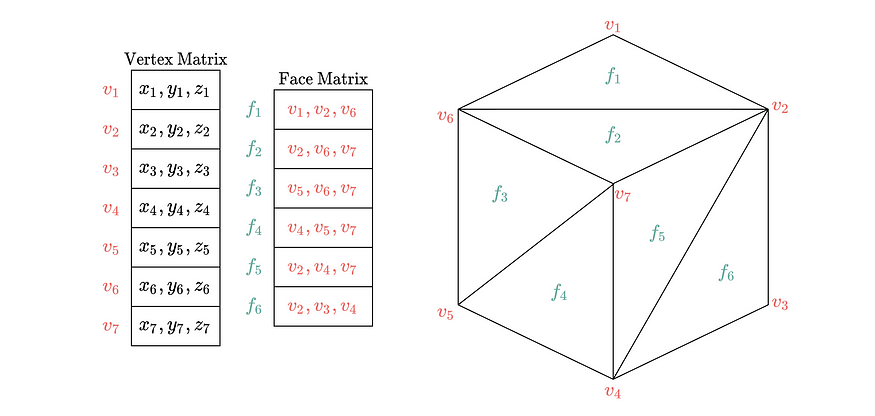
Note that the vertex matrix captures node-level feature information and the face matrix describes the node connectivity. Formally, each mesh can be transformed into a graph G = (X, A) with vertices V, where X has dimension (|V|, 3) and defines the spatial xyz-features for each node u in V, and A, the adjacency matrix, has dimension (|V|, |V|) and defines the connected neighborhood of each node. We work with this induced mesh graph.
注意,顶点矩阵捕获节点级特征信息,而面矩阵描述了节点连接性。形式上,每个网格可以转换为图 G = (X, A),其中 V 是顶点集,X 的维度为 (|V|, 3),定义了每个节点 u 在 V 中的空间 xyz 特征,而邻接矩阵 A 的维度为 (|V|, |V|),定义了每个节点的连接邻域。我们使用这个诱导网格图。
Implementation 实现
We rely on Feature-Steered graph convolutions to derive node-level body-part assignments from the induced mesh graph. This GCN layer was proposed by Verma et al. [1].
我们依赖于特征引导的图卷积来从诱导网格图中推导出节点级的身体部位分配。这个 GCN 层由 Verma 等人提出 [1]。
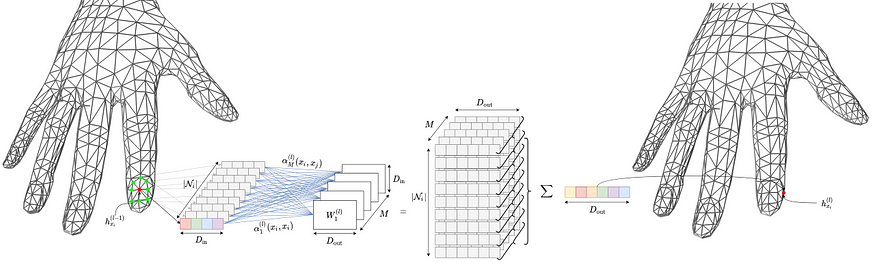
A node-level embedding update via Feature-Steered graph convolution.
通过特征引导的图卷积进行节点级嵌入更新。
The Feature-Steered graph convolution works as follows. The embedding of the central node (in red) is updated by aggregating transformed embeddings of neighboring nodes (in green) as well as transformed embedding of itself. In particular, M different messages are created for each node by passing its embedding through M weight matrices. Therefore, a total of M x Ni messages are created. These M x Ni are aggregated via a tunable weighted average. This can be expressed as:
特征引导的图卷积工作原理如下。中心节点(红色)的嵌入通过聚合相邻节点(绿色)的转换嵌入以及自身的转换嵌入来更新。具体来说,通过将每个节点的嵌入传递给 M 个权重矩阵来为每个节点创建 M 条消息。因此,总共创建了 M x Ni 条消息。这些 M x Ni 条消息通过可调的加权平均进行聚合。这可以表示为:
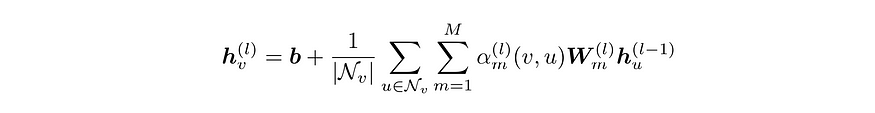
where Nv is the set of adjacent vertices (neighbors) of vertex v (including v itself).
其中 Nv 是顶点 v 的相邻顶点集(包括 v 本身)。
The M messages are weighted via a learnable attention mechanism. These are computed for each layer as follows:
这些 M 条消息通过可学习的注意力机制进行加权。它们按以下方式为每一层计算:
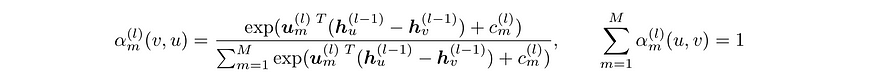
where u and c are learnable parameters, specific to each layer. Note that this attention weight function is translation invariant, which is desirable when working with spatial input features. It ensures that the translation of an input mesh does not affect the computed attention weights.
其中 u 和 c 是特定于每一层的可学习参数。请注意,这个注意力权重函数是平移不变的,这在处理空间输入特征时是理想的。它确保输入网格的平移不会影响计算出的注意力权重。
PyG 中的实现
This graph convolution operation can be implemented using the PyTorch geometric (PyG) message passing class. Three class methods define a PyG message passing class. These are forward (performs a forward pass), message (constructs the node-level messages) and aggregate. The message and forward function are defined below:
这个图卷积操作可以使用 PyTorch geometric (PyG) 的消息传递类https://pytorch-geometric.readthedocs.io/en/latest/notes/create_gnn.html#the-messagepassing-base-class来实现。三个类方法定义了一个 PyG 消息传递类。这些是 forward (执行前向传递)、 message (构建节点级消息)和 aggregate 。 message 和 forward 函数定义如下:




Network Architecture 网络架构
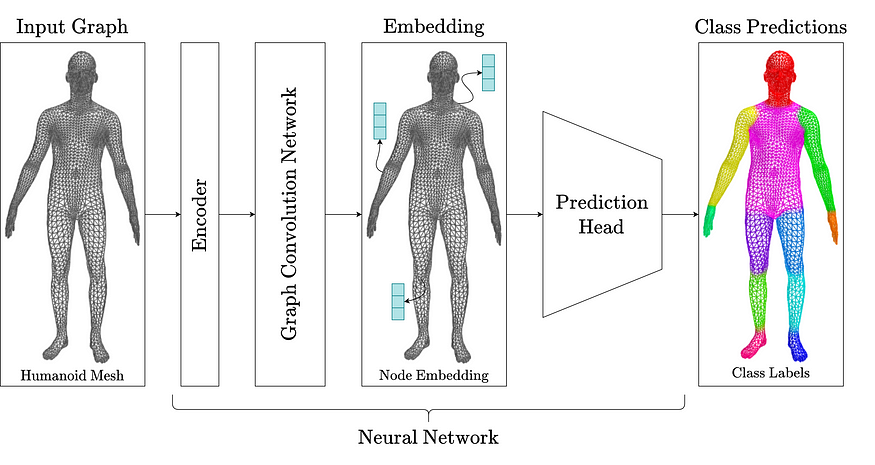
The Feature-Steered graph convolution forms the backbone of our body-part labeling network. Our general network architecture is as follows:
特征引导的图卷积构成了我们身体部位标记网络的核心。我们的一般网络架构如下:
A multilayered perceptron encoder is first used to embed the node-level input feature vectors (xyz coordinates).
首先使用多层感知机编码器来嵌入节点级输入特征向量(xyz 坐标)。
The encoded node-level features are then sequentially passed through four Feature-Steered convolutional layers. These layers each aggregate messages from 12 attention heads (the number of body-part output labels).
编码后的节点级特征随后被顺序传递给四个特征引导的卷积层。这些层每个都从 12 个注意力头(即身体部位输出标签的数量)聚合消息。
Finally, the refined node-level features are passed through a prediction head, namely a multi-perceptron prediction. It outputs a soft class correspondence for each node.
最后,精细化的节点级特征被传递给一个预测头,即一个多感知器预测。它为每个节点输出一个软类别对应关系。
We train the neural network to minimize the cross-entropy loss between the predictions and the ground-truth segmentation labels. This loss is back-propagated through the entire network to update the parameters. The resulting training loop is defined below:
我们训练神经网络以最小化预测与真实分割标签之间的交叉熵损失。该损失通过整个网络反向传播以更新参数。由此产生的训练循环定义如下:
| def train(net, train_data, optimizer, loss_fn, device): | |
| for | |
| return |
mesh-seg-train.py
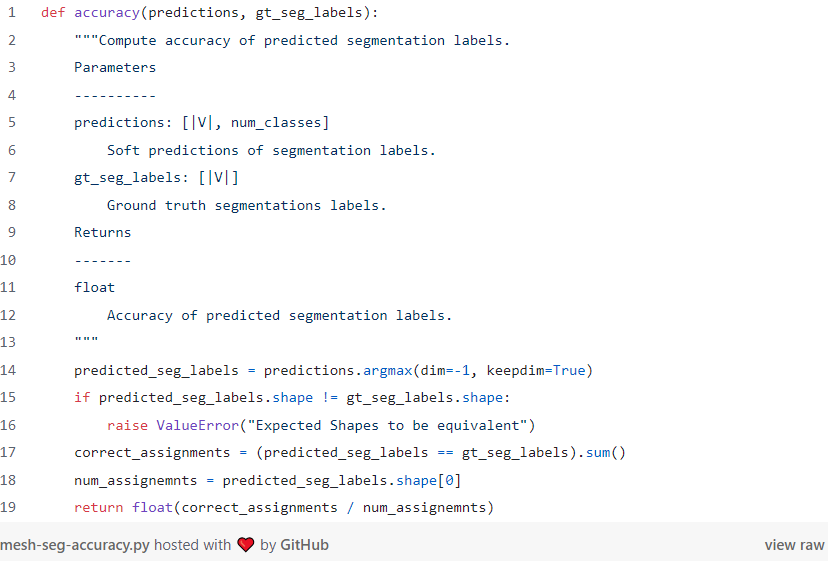
Finally, we evaluate the network’s performance by computing the accuracy between the predicted and ground-truth segmentation lbels. This computation is shown below:
最后,我们通过计算预测与真实分割标签之间的准确率来评估网络性能。该计算如下所示:
数据集
We train our network on the MPI FAUST data-set [2]. It contains 100 watertight humanoid meshes. We generated segmentation labels by labeling a single mesh. These labels were transferred to all other meshes via ground-truth vertex correspondences included in the data-set. We use 80 meshes to train our neural network, and evaluate on 20 meshes.
我们在 MPI FAUST 数据集[2]上训练我们的网络。该数据集包含 100 个水密的人形网格。我们通过标记单个网格生成了分割标签。这些标签通过数据集中包含的真实顶点对应关系转移到所有其他网格。我们使用 80 个网格来训练神经网络,并在 20 个网格上进行评估。

10 poses of the humanoid meshes in the MPI FAUST data-set.
MPI FAUST 数据集中的人形网格的 10 个姿势。
The network’s learning process on this dataset is visualized below. We see the class predictions converging to the correct body part label. The trained network achieved an accuracy of 95% on the test dataset.
该数据集上的网络学习过程如下所示。我们看到类别预测收敛到正确的身体部位标签。训练后的网络在测试数据集上达到了 95%的准确率。

结论
In conclusion, we showed how to generalize the convolution operation from regular graphs defined on the Euclidean space to irregular graphs with arbitrary connectivity. This generalization led us to define GCNs, an extension of CNNs. Unlike traditional CNNs, GCNs can operate on irregular graphs. Thus, GCNs can be applied to diverse data — meshes as we illustrated, molecules, social networks, and even 2D images.
总之,我们展示了如何将卷积操作从定义在欧几里得空间上的规则图推广到具有任意连接性的不规则图。这种推广使我们定义了 GCN,即卷积神经网络的扩展。与传统的 CNN 不同,GCN 可以在不规则图上操作。因此,GCN 可以应用于各种数据——正如我们所展示的网格,分子,社交网络,甚至 2D 图像。
参考文献
[1] Nitika Verma, Edmond Boyer, and Jakob Verbeek. FeaStNet: Feature-Steered Graph Convolutions for 3D Shape Analysis. 2018. arXiv: 1706.05206 [cs.CV].
[2] Federica Bogo et al. “FAUST: Dataset and evaluation for 3D mesh registration”. In: Proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR). Piscataway, NJ, USA: IEEE, June 2014



内容中包含的图片若涉及版权问题,请及时与我们联系删除




评论
沙发等你来抢