博士论文 | Oxford 2025 | 流形假设下的贝叶斯非参数估计 248页

随着近年来可用数据量的急剧增长，无论是在样本数量（大 nnn）还是预测变量数量（大 ppp）方面，开发适用于大规模统计方法的方法论与理论理解已成为一个紧迫课题。虽然“大样本”主要带来了计算层面的问题，但“高维预测变量”则引出了特定的统计问题，即所谓的“维度灾难”。在本论文中，我们研究了流形假设——即高维预测变量往往蕴含未知的低维结构——如何在此背景下提升贝叶斯非参数估计方法的统计收敛性。

在本论文的引言部分，我们将介绍后续章节中用于解决上述问题的数学工具。我们首先在第 1.1 节回顾微分几何与黎曼几何中的基本概念，重点关注欧几里得空间中的子流形结构。接着在第 1.2 节中，我们介绍紧子流形与有限图的谱理论基础，并展示随机图如何对未知子流形进行有效逼近。在第 1.3 节，我们介绍贝叶斯非参数统计中用于推导后验收缩率的关键证明技巧。最后，第 1.4 节将综述与第 2、3 和 4 章所研究问题相关的非参数估计理论的当前研究进展。

作为一篇综合性博士论文，第 2、3 和 4 章分别包含已发表或已提交待审的研究论文。在第 2 与第 3 章中，我们研究协变量支持在未知子流形上的非参数回归问题。我们针对一类此前研究较少的方法，推导出仅依赖于数据内在维度的后验收缩率。在第 4 章中，我们将重点研究概率分布支持在未知子流形附近的密度估计问题，设计一类新的非参数高斯混合模型，并推导其对应的后验收缩率，同时也介绍该方法的实现细节。

最后，第 5 章对全文进行总结与讨论。

论文题目：Bayesian Nonparametric Estimationunder the Manifold Hypothesis

作者：Paul Rosa

类型：2025年博士论文

学校：University of Oxford（英国牛津大学）

下载链接：

链接: https://pan.baidu.com/s/1UMLtaRJoJx8znB7a22ynjw?pwd=gdh4

硕博论文汇总：

链接: https://pan.baidu.com/s/1Gv3R58pgUfHPu4PYFhCSJw?pwd=svp5

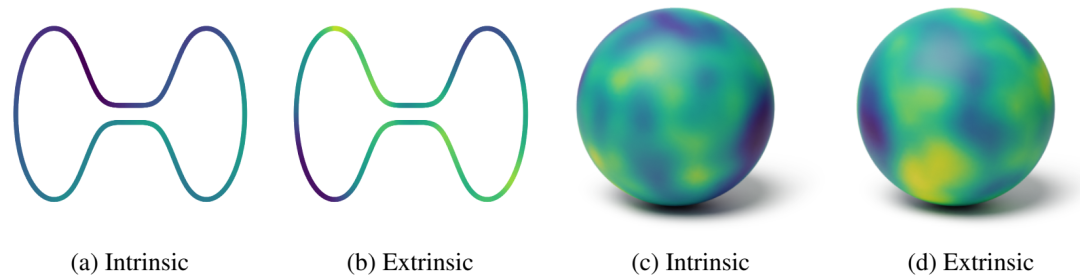
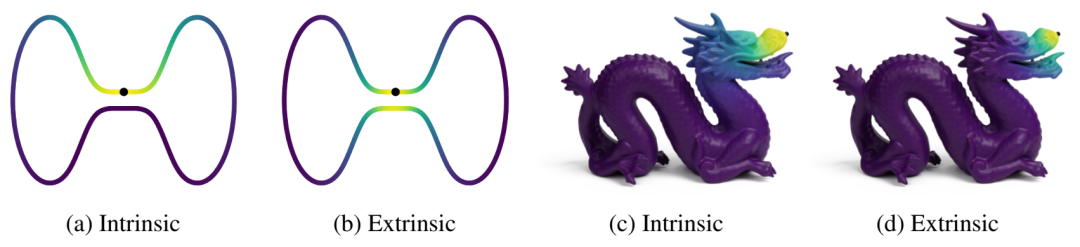
来自不同歧管上不同Matérn高斯过程的样品，即一维哑铃形歧管和二维球体。注意值在（a）中的固有过程中，整个哑铃的瓶颈都可能大不相同非常接近环境欧几里得距离，与外在模型的情况形成对比（b）。另一方面，（c）和（d）之间几乎没有质量区别，因为嵌入在球体上的地球距离产生了合理良好的全球近似值。

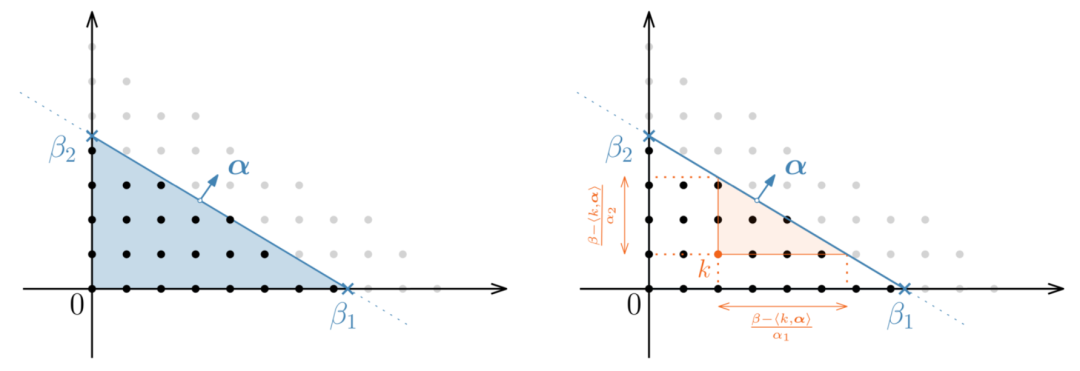
尺寸d = 2的一个示例。矢量α是唯一具有正坐标的向量，并且与顶点{βiei}1≤i≤D的单纯形正交。黑色是N2的点K例如<k，α> <β。

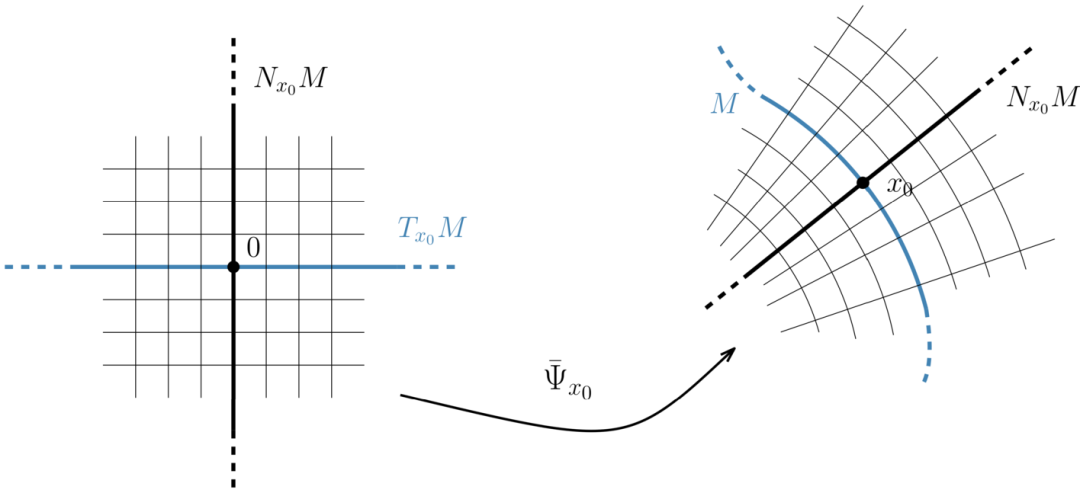
参数化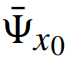的视觉解释。

（左）一个限制的平滑子延伸的示例大于τ，并且（右）是此类歧管的有限结合。这两个子集都是可以接受的，因为（接近）支持密度F0满足命题3.2的收缩率。

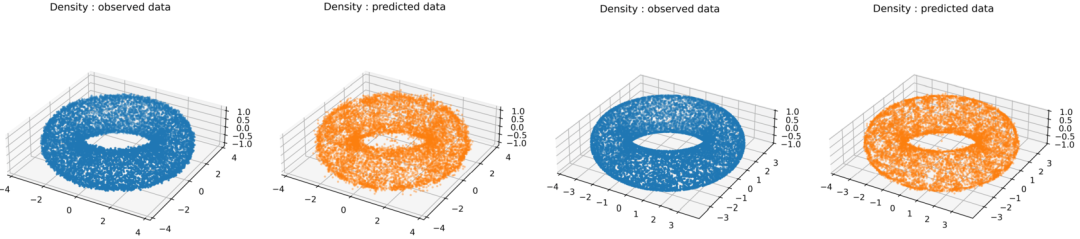
与图6相同的实验，对于n = 10000点的圆环，并进行了采样，并且（剩下两个图）δ= 0.5和（右两个图）δ= 0.05。

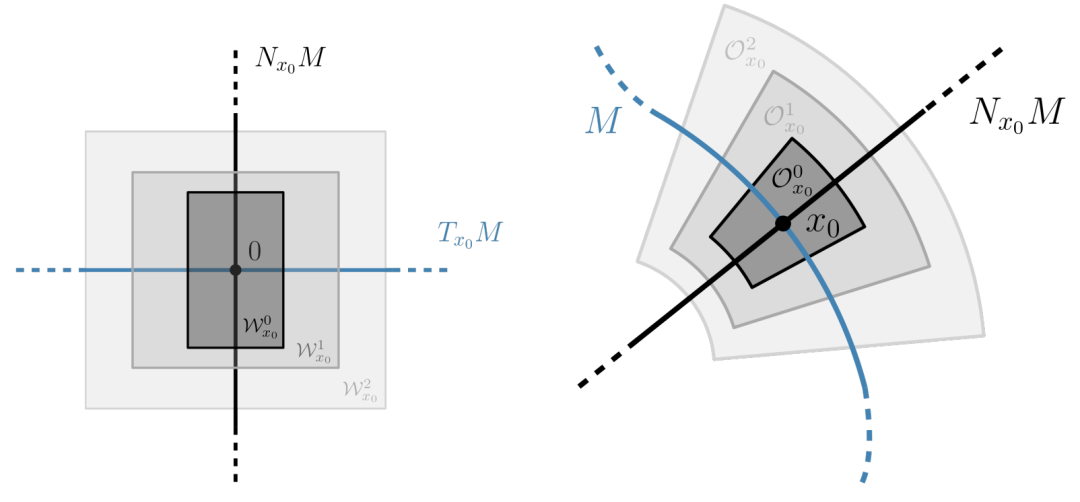
第3节证明中使用的集合的视觉表示。

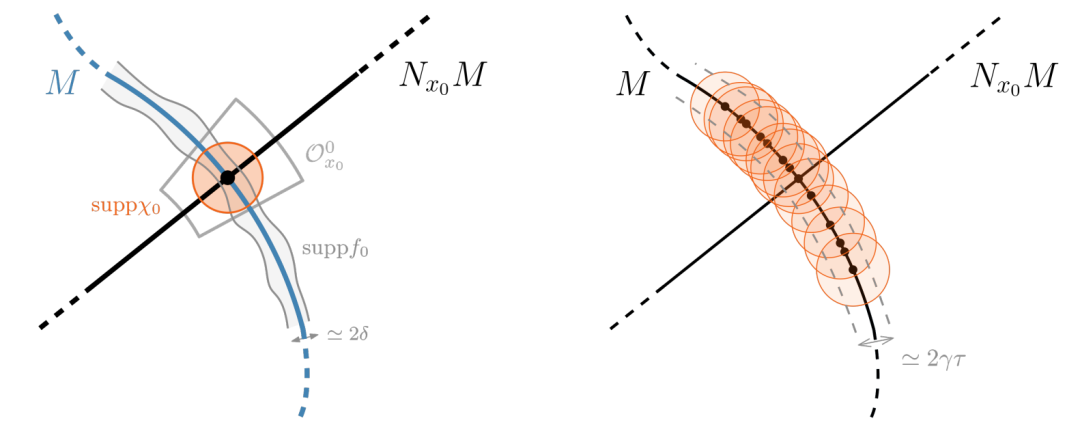
引理S1.4的框架和结果的视觉解释。