小满 | 两人一起可以解决离散对数问题吗？

自从 RSA 公钥加密发明以来，密码学家发掘了很多数学问题，他们被公认为在算法上难以高效地解决。这些问题的难解性被称作密码学假设，依赖于这些假设，密码学家们构造了丰富的密码学协议。

各种各样的假设支撑起了现代密码学世界，其中最重要的之一就是离散对数问题（Discrete Logarithm Problem）：

对于一个（乘法）循环群  和其生成元 ，从  中随机选取出一个元素 ，求  使得  。

对于一部分精心选取的、可以用  比特表示的群 ，目前人们还没有找到  时间的算法。

而另一方面，由  和  计算出  是很高效的，利用这种“单向性”，人们可以构造公钥加密、数字签名等等。

粗略地讲，我们可以把  看作  的“加密”——坏人很难从密文  看出消息 。这种加密还有一种额外的好处：两条密文的乘积就是两条消息之和的加密——，密码学家们称之为（加法）同态加密。可惜的是，除了本来就知道  的人，没有任何人可以从密文  中获得任何信息——即使是可信的人也不例外，这种加密没有意义。

在2016年，Elette Boyle，Niv Gilboa 和 Yuval Ishai 合作提出了分布式离散对数算法（Distributed Discrete Logarithm）。该算法使得在两个人参与的情况下，不仅可以做指数“加密”，还可以共同从“密文”中还原信息。他们利用这一技术构造了一种双方安全计算协议（Secure 2-Party Computation protocol），其渐进通信复杂度亚线性依赖于要计算的电路大小——在此之前仅有全同态加密（Fully Homomorphic Encryption）等少数几个高级密码学工具可以做到。该文章也获得了2016年 CRYPTO 会议的最佳论文奖。

图源：网络

‘两人共同从“密文”中还原信息’是什么意思呢？这要从秘密分享（Secret Sharing）说起。秘密分享是一种很常用的隐私计算方式，假设一条消息 ，我们选取随机值 ，令 ，然后让两个人（Alice 和 Bob）分别拿着 和 ，这样，只要 Alice 和 Bob 不合谋，两个人就都无法获知 。我们称 这种形式为（加法群上的）加法分享（Additive Sharing），那么自然地也有（乘法群上的）乘法分享（Multiplicative Sharing），形如： 。加法（乘法）秘密分享也具有加法（乘法）同态性质：两条消息的加法（乘法）分享的和（乘积）恰好构成这两条消息之和（积）的分享。

回到离散对数问题里，假设 Alice 和 Bob 初始时加法分享了一个消息 ，他们分别持有 和 ，当他们各自做指数“加密”后，分别持有 和 ，它们构成  的乘法分享。分布式离散对数的关键就是，Alice 和 Bob 可以仅仅通过本地计算（无交互），就将乘法分享再次变回加法分享。

首先，Alice 和 Bob 可以事先在整个乘法群   中约定好一些元素，这些元素最好比较均匀地分布在整个群中，并且数量不能过多也不能过少，接下来 Alice 和 Bob 分别从 和 出发，每次乘 ，直到遇到一个约定好的元素，并记录乘了多少次 。假设他们碰到的恰好是同一个约定好的的元素 ，那么 Alice 和 Bob 记录的次数就分别是 和 ，它们恰好构成  的加法分享。

注意到，如果这些约定好的元素太少，以至于在整个群中的分布非常稀疏，那么 Alice 和 Bob 就要走很久才可以碰到一个约定元素，算法的运行时间会过长；另一方面如果约定的元素太多，则会有较大的概率 Alice 和 Bob 碰到的不是同一个约定元素，算法的正确性就会被破坏。因此 Boyel，Gilboa 和 Ishai 精心选取了参数使得保证算法运行时间  的同时，错误概率  ——尽管这不是太理想。

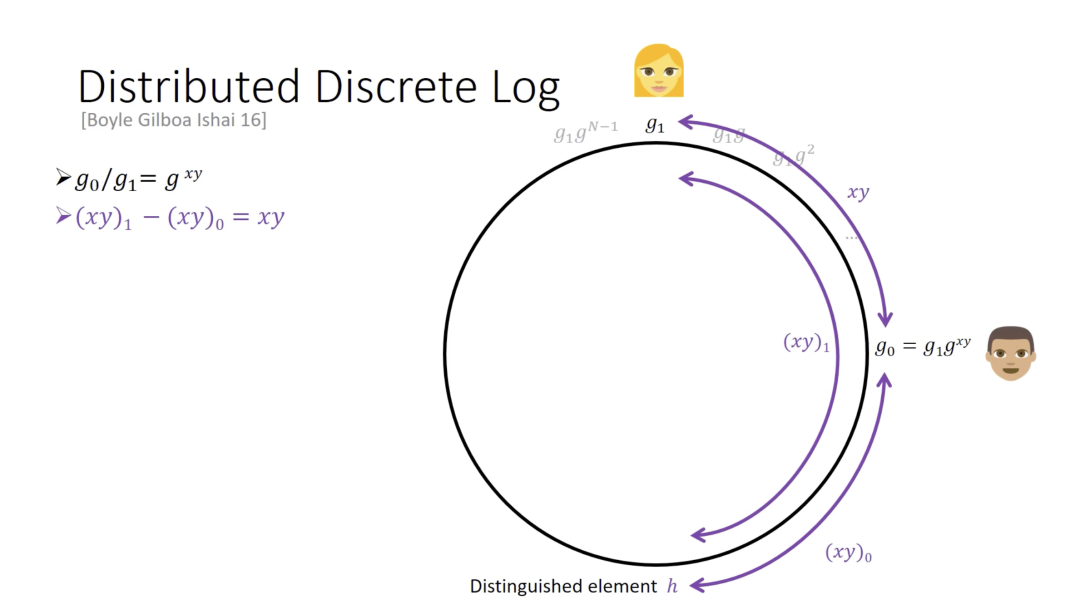
图源：Peter Scholl 在 EUROCRYPT 2021 的 talk slides

利用这种从乘法分享到加法分享的转换，以及分享和指数的同态性质，Boyel，Gilboa 和 Ishai 构造了一个具有空前计算能力的同态秘密分享方案（Homomorphic Secret Sharing）——Alice 和 Bob 在拿到各自的分享后，可以通过仅在本地做运算，得到消息的函数值的分享，即  ，其中  属于某种受限的代数函数。

在接下来的几年中，众多密码学家将这一思想拓展到各种不同的公钥假设和加密方案中（BGI16 实际上使用的是依赖于 Decisional Diffie-Hellman (DDH) 假设的加密而非简单的指数，在此为了说明容易将其简化），得到了依赖多种假设的同态秘密分享方案。比如 Elette Boyle，Lisa Kohl 和 Peter Scholl 将其拓展到了 Learning with Errors (LWE) 假设，Claudio Orlandi，Peter Scholl，Sophia Yakoubov，Lawrence Roy 和 Jaspal Singh 将其拓展到了依赖于 Decisional Composite Residuosity (DCR) 假设的 Paillier 加密和 Damgard-Jurik 加密，都获得了更高效的构造。

此外，人们很快发现分布式离散对数这一工具的强大，并将其利用在诸多密码学方案的构造中。如今，每年都会产生出很多使用分布式离散对数的新成果，它的力量已经延伸到密码学的众多领域。

[1] Elette Boyle, Niv Gilboa, and Yuval Ishai. Breaking the circuit size barrier for secure computation under DDH. In Matthew Robshaw and Jonathan Katz, editors, CRYPTO 2016, Part I, volume 9814 of LNCS, pages 509–539. Springer, Berlin, Heidelberg, August 2016.

[2] Elette Boyle, Lisa Kohl, and Peter Scholl. Homomorphic secret sharing from lattices without FHE. In Yuval Ishai and Vincent Rijmen, editors, EUROCRYPT 2019, Part II, volume 11477 of LNCS, pages 3–33. Springer, Cham, May 2019.

[3] Claudio Orlandi, Peter Scholl, and Sophia Yakoubov. The rise of paillier: Homomorphic secret sharing and public-key silent OT. In Anne Canteaut and François-Xavier Standaert, editors, EUROCRYPT 2021, Part I, volume 12696 of LNCS, pages 678–708. Springer, Heidelberg, October 2021.

[4] Lawrence Roy and Jaspal Singh. Large message homomorphic secret sharing from DCR and applications. In Tal Malkin and Chris Peikert, editors, CRYPTO 2021, Part III, volume 12827 of LNCS, pages 687–717, Virtual Event, August 2021. Springer, Cham.

文 | 刘立强