刻画同步相变：广义Kuramoto模型的临界性与普适性丨5月23-24日（周五-六）直播 · 第9-10期复杂网络动力学读书会

集智俱乐部 2025年05月20日 21:29 上海

导语

我们身处的世界充满了由大量相互作用的单元构成的复杂系统，单元的相互协调往往会涌现出令人惊叹的集体行为模式。同步便是其中最普遍的一种。同步，作为非平衡集体行为中最基本、最普遍的形式之一，描述了系统如何通过内部单元间的微观耦合，自发地达到宏观节律上的一致性。

Kuramoto 模型在此问题上扮演了核心角色，提供了一个简洁而深刻的数学框架以回答这个重要问题：一群拥有不同自然频率的个体，如何通过耦合作用克服彼此的“个性”，最终达成步调一致？

这个过程，本质上是一种同步相变——系统从无序的混乱状态，自发地转变为宏观有序的协同状态。理解这种秩序如何从无序中涌现，是理解复杂系统集体行为的关键。然而，如果单元具有更复杂的对称性（维度D），且相互作用受空间维度 d 限制。那么，同步相变的普适规律如何被D和d共同影响？哪个因素更关键？

「复杂网络动力学」读书会第九期将由北京师范大学博士生邱仲普分享，将尝试回答这一问题。我们研究广义了 Kuramoto 模型，系统考察对称性D和空间维度d对同步临界特性的塑造作用。核心发现是：对偶数D，同步相变的普适性，不依赖于单元内部复杂性D，却强烈依赖于空间维度d。这项工作为理解非平衡系统的普适性，特别是空间维度与对称性如何控制集体行为，提供了更清晰统一的物理框架。由于内容十分丰富，读书会将分为两期，分别于5月23日（本周五）以及5月24日（本周六）19:30-21:30进行，欢迎感兴趣的朋友参与讨论交流！

分享简介简介

一群拥有不同自然频率的个体达成步调一致的过程，本质上是一种同步相变——系统从无序的混乱状态，自发地转变为宏观有序的协同状态。理解这种秩序如何从无序中涌现，是理解复杂系统集体行为的关键。

刻画同步相变的关键物理量包括：临界指数，普适类和临界维数。对于经典的耦合Kuramoto振子系统，前人对其中的部分问题有所探索。

然而，如果单元具有更复杂的内秉维度D，且相互作用受空间维度d限制。那么，同步相变的临界指数和普适类如何被D和d共同影响？本次报告将尝试回答这一问题。我们研究了广义的Kuramoto模型，系统考察内秉维度D和空间维度d对同步临界特性的塑造作用。

我们在完全图和d维晶格上探索了偶数D维广义Kuramoto振子中的同步相变。

第九期：全局耦合系统中的同步相变（5.23）

在全局耦合系统中，通过对于自洽方程的解析展开，结合有限尺寸标度修正，揭示了对于所有偶数D的普适临界指数β=1/2和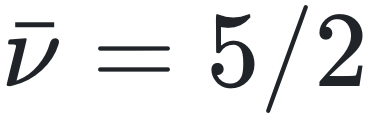，表明了其中存在一个非常规的上临界维数d_u=5。针对多个偶数D的大量数值模拟证实了这些理论预测。

第十期：局域耦合系统中的同步相变（5.24）

承接上期，对于局部耦合系统，我们开发了一个基于自旋波理论和基于时间序列建立功能网络技术的框架，该框架可以捕捉到夹带转变（Entrainment transition）中的临界性。修正的Edwards Anderson序参数进一步验证了预测的指数。这项理论和数值研究相结合，揭示了一个依赖于内秉自由度D但依赖于空间维数d的临界性为特征的普适类族。这项工作为理解非平衡系统的普适性，特别是空间维度与对称性如何控制集体行为，提供了清晰统一的物理框架。

分享内容大纲

第九期：全局耦合系统中的同步相变（5.23）

同步与Kuramoto模型

经典Kuramoto模型的临界指数

D维Kuramoto模型(DDKM)及其动力学特性

D维Kuramoto模型临界指数的理论分析(全局耦合情形)

数值验证

第十期：局域耦合系统中的同步相变（5.24）

广延系统中同步行为的维度依赖性（局部耦合情形）

基于时间序列建网的夹带集群识别算法

广义EA序参量

同步误差与线性自旋波近似理论

主要涉及到的知识概念

第九期：全局耦合系统中的同步相变（5.23）

Kuramoto模型， Kuramoto model

同步相变， Synchronization transition

临界指数， Critical exponents

普适类， Universality class

临界维数， Critical dimension

D维Kuramoto模型， D-dimensional Kuramoto model

第十期：局域耦合系统中的同步相变（5.24）

自旋波近似， Spin wave approximation

时间序列建网技术， Time-series-based network construction technique

EA序参量， Edwards-Anderson (EA) order parameter

相关概念解释

1. 同步与模型类

• Kuramoto模型（Kuramoto Model）定义：描述耦合振子同步现象的经典数学模型，通过相位动力学方程刻画个体相互作用下的集体节律锁定行为。领域：非线性动力学、统计物理、复杂系统。扩展：D维仓本模型（D-dimensional Kuramoto Model, DDKM）将传统单相位振子推广至高维内秉自由度（维度D），用于研究多维同步机制。

• 同步相变（Synchronization Transition）定义：多体系统从无序异步态向宏观同步态转变的非平衡相变现象，伴随着非零序参量的涌现。特征：可通过临界指数（如β, ν）描述的普适类（Universality Class）分类。

2. 临界现象理论

• 临界指数（Critical Exponents）定义：刻画系统在相变点附近标度行为的无量纲参数（如序参数随控制变量的幂律标度指数β）。作用：区分不同系统的普适类，反映微观机制对宏观临界行为的决定性。

• 普适类（Universality Class）定义：具有相同临界指数集合的相变的抽象，其临界行为仅依赖系统维度、对称性等全局特征，而非微观细节。

• 临界维数（Critical Dimension）定义：决定系统临界行为是否受涨落显著影响的空间维度阈值。上临界维数（Upper Critical Dimension, d_u）：高于此维度时，系统临界行为可用平均场理论准确描述（如本研究发现的d_u=5）。

3. 分析方法与技术

• 自旋波近似（Spin Wave Approximation）定义：处理连续对称性破缺系统低能激发的理论方法，通过对动力学进行线性化以解析集体模式（如相位波）。应用：局域耦合系统中同步相变的临界行为分析。

• 时间序列建网技术（Functional Network Reconstruction from Time Series）定义：基于动态时间序列数据构建节点间关联网络，通过网络分析解释系统行为模式。例子：气候网络。

• 夹带集群（Entrainment Clusters）定义：振子群体在外部驱动或内部耦合下形成局部频率同步的动力学模块，其规模与耦合强度及拓扑结构相关。

4. 序参量与系统分类

• EA序参量（Edwards-Anderson Order Parameter）起源：自旋玻璃理论中描述无序磁性系统冻结态局部磁化强度的参量。推广：本研究修正后用于量化非平衡同步系统中局部entrainment 程度，反映空间关联与动态异质性。

• 全局耦合（Global Coupling）定义：系统中所有个体均以相同强度全连接直接相互作用（也就是完全图拓扑）。

• 局部耦合（Local Coupling）定义：个体仅与有限空间邻域内的其他个体相互作用（如晶格拓扑）。

5. 系统类型

• 广延系统（Extended Systems）定义：具有空间广延性的多体系统（如一维链、二维晶格等）。

讲者介绍

邱仲普，北京师范大学系统科学学院系统理论专业博士生，导师为樊京芳教授。本科就读于四川大学物理学（试验班）专业，曾入选2018年度基础学科拔尖学生培养试验计划（珠峰计划）。主要从事相变与临界现象、复杂网络上的同步与涌现动力学、地球系统复杂性与临界性分析、AI4Climate等方面的研究。

参考文献

第九期：全局耦合系统中的同步相变（5.23）

1. Acebrón, J. A., Bonilla, L. L., Pérez Vicente, C. J., Ritort, F. & Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys.77, 137–185 (2005).

2. Hong, H., Chaté, H., Park, H. & Tang, L.-H. Entrainment Transition in Populations of Random Frequency Oscillators. Phys. Rev. Lett.99, 184101 (2007).

3. Tang, L.-H. To synchronize or not to synchronize, that is the question: finite-size scaling and fluctuation effects in the Kuramoto model. J. Stat. Mech.2011, P01034 (2011).

4. Hong, H., Chaté, H., Tang, L.-H. & Park, H. Finite-size scaling, dynamic fluctuations, and hyperscaling relation in the Kuramoto model. Phys. Rev. E92, 022122 (2015).

5. Daido, H. Susceptibility of large populations of coupled oscillators. Phys. Rev. E91, 012925 (2015).

6. Chandra, S., Girvan, M. & Ott, E. Continuous versus Discontinuous Transitions in the D-Dimensional Generalized Kuramoto Model: Odd D is Different. Phys. Rev. X9, 011002 (2019).

第十期：局域耦合系统中的同步相变（5.24）

1. Fan, J. et al. Statistical physics approaches to the complex Earth system. Physics Reports896, 1–84 (2021).

2. Chandra, S., Girvan, M. & Ott, E. Continuous versus Discontinuous Transitions in the D-Dimensional Generalized Kuramoto Model: Odd D is Different. Phys. Rev. X9, 011002 (2019).

3. Hong, H., Chaté, H., Park, H. & Tang, L.-H. Entrainment Transition in Populations of Random Frequency Oscillators. Phys. Rev. Lett.99, 184101 (2007).

4. Tang, L.-H. To synchronize or not to synchronize, that is the question: finite-size scaling and fluctuation effects in the Kuramoto model. J. Stat. Mech.2011, P01034 (2011).

5. Hong, H., Chaté, H., Tang, L.-H. & Park, H. Finite-size scaling, dynamic fluctuations, and hyperscaling relation in the Kuramoto model. Phys. Rev. E92, 022122 (2015).

报名参与读书会