导语
物理系统中存在一些的基本定律和原理，决定着系统的演化极限。兰道尔原理便是其中之一，它限制了计算系统中擦除 1 bit 信息所需的最小能量。兰道尔原理通过在 “信息” 和可物理测量的值之间架起一座桥梁，为 “万物源于比特” 的观点提供了可测量的物理内容。但兰道尔原理是独立于热力学第二定律的更严格的极限吗？学界仍在进行持续探索。
本文是主题专刊《热力学2.0：连接自然科学与社会科学（第一部分）》的一部分。
关键词：兰道尔原理，热力学第二定律，兰道尔极限
Edward Bormashenko丨作者
周莉丨译者
以色列阿里埃勒大学工程科学院化学工程、生物技术与材料系；
“在基本概念的适用范围内，热力学是唯一具有普遍意义的物理学理论，我坚信它永远不会被推翻。”
—— 阿尔伯特・爱因斯坦（Albert Einstein）
计算机的迅速发展引发了人们对计算物理基础的浓厚兴趣。这种兴趣源于计算在应用和基础研究两方面的重要性[1]。有人提出假设，整个宇宙可以被看作是一台巨大的量子计算机（Quantum computer）[2]。可以说，甚至自然演化也能被视为一种利用材料物理特性的计算过程[3]。从最普遍的意义上讲，计算是指使用一组特定指令将输入转化为输出。在物理系统下，数字计算机则被看作是一种物理设备，它通过将逻辑单元 “打开” 和 “关闭” 来处理比特（bit），这些物理变化就是计算过程[4]。物理系统的行为存在一些基本定律和原理，基于此我们可以知道计算的基本极限：计算的物理极限（最小能量消耗）是多少？计算的最大可能速度又是多少[5]？以及在特定情况下，是否有可能突破这些基本极限呢？
物理系统中存在一些决定系统极限的基本定律和原理[5-7]，包括阿贝衍射极限（Abbe diffraction limit）[8]和海森堡不确定性原理（Heisenberg uncertainty principle）[9]。将光在真空中传播的极限速度 c 与海森堡不确定性原理相结合，就得到了布雷默曼极限（Bremermann’s limit），它决定了一个自包含系统（Self-contained system）能够实现的最大计算速率进行了限制[10]。量子力学还产生了曼德尔斯坦姆 - 塔姆（Mandelstam–Tamm）和马戈勒斯 - 莱维廷（Margolus–Levitin）极限原理，这些原理限制了量子系统动力学演化的最大速度[11-13]。
注：自包含系统指（Self - contained system）是指在特定研究或讨论情境下，能在内部完成特定功能且基本不依赖外部因素干扰就能维持自身运行和实现目标的系统，具有独立性、完整性和封闭性特点。
本期特刊讨论的兰道尔原理（Landauer’s principle），是限制计算系统行为的物理原理之一。它对擦除 1 bit 信息所需的最小能量进行了限制。理论提出者罗尔夫・兰道尔（Rolf Landauer）认为，计算是一个物理过程，因此它一定遵循物理定律，尤其是热力学定律[14-17]。通过计算在平衡温度 T 下运行的系统擦除 1 bit 内存的最小能量成本，可以通过公式（1）计算：
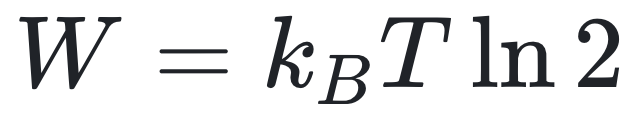
兰道尔原理还在逻辑不可逆性和热力学不可逆性之间做出了至关重要的区分[18]。需要强调的是，公式（1）中的兰道尔极限（Landauer bound）仅适用于整个计算系统中一个能够独立携带信息的最小单元。兰道尔原理是在没有直接引用热力学第二定律的情况下，经过严格的微观推导得出的[19]。兰道尔原理在量子力学领域的扩展也已得到证实[20, 21]。此外，兰道尔原理也在相对论[22, 23]和多值逻辑系统[24]中得到推广。
注：逻辑不可逆性指的是在计算过程中，你丢失了一些信息，导致你无法仅仅通过计算结果来完全恢复原始的输入。比如你输入了 3 和 5，得到了 8，但你不能通过8确定原始输入的数字是3和5。
将兰道尔极限与马戈勒斯 - 莱维廷极限原理（Margolus–Levitin limiting principle）相结合，可以得出设备进行单次计算操作所需的最短时间[7]。单次计算所需的最短 “马戈勒斯 - 莱维廷 - 兰道尔” (Margolus–Levitin–Landaue)时间τMLL 由公式（2）给出：
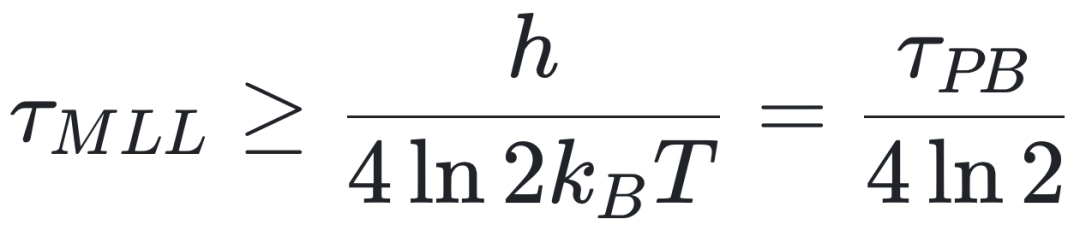
其中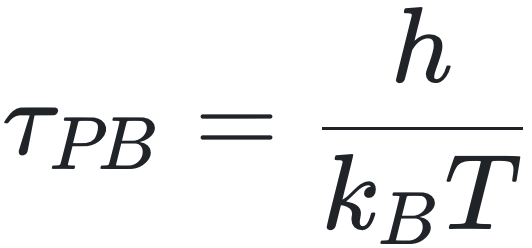
是普朗克 - 玻尔兹曼热化时间（Planck–Boltzmann thermalization time），被认为是给定系统热化的最快弛豫时间尺度[25]。
兰道尔原理可以在约翰・阿奇博尔德・惠勒（John Archibald Wheeler）提出的 “万物源于比特（It from bit）” 这一整体概念框架内进行解释。“万物源于比特” 意味着物理世界的每一个事物在根本上都有一个非物质的来源和解释；我们所说的现实归根结底来自于对是非问题的提出以及对设备引发的响应的记录；简而言之，所有物理事物在起源上都与信息论相关，这是一个参与性的宇宙[26]。兰道尔原理通过在 “信息” 和可物理测量的值之间架起一座桥梁，为 “万物源于比特” 的观点提供了可测量的物理内容。这座桥梁在最近的一系列论文中得以构建[22, 23, 27-29]。根据埃雷拉（Herrera）的研究[22]，改变 1 bit 信息会使系统质量减少，减少的最小量由公式（3）给出：
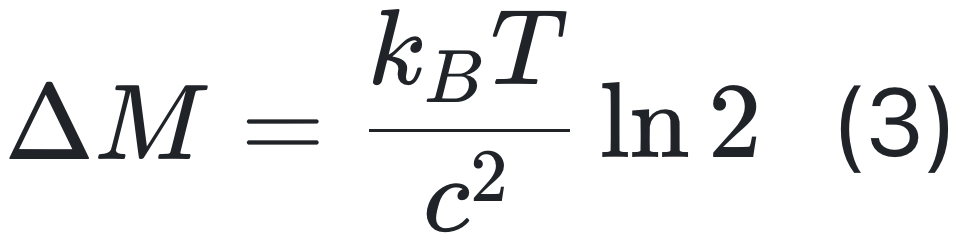
已有研究报道了兰道尔原理在逻辑不确定操作和非平衡系统中的推广[30, 31]。兰道尔极限也在多项实验研究中得到了成功验证[32-34]。尽管如此，兰道尔原理的含义和表述仍受到了激烈的批评。有人认为，由于它并非独立于热力学第二定律，所以它既不是解决麦克斯韦妖（Maxwell’s Demon）问题的必要条件，也不是充分条件[35]。拉雷兹（Lairez）提出了一个物理实现的反例（该反例利用了逻辑状态和热力学状态之间的二对一关系），表明可以以热力学准静态的方式擦除 1 bit 信息[36]。布福尼（Buffoni）等人证明，与普遍观点相反，兰道尔原理既不是热力学第二定律，也不等同于它，实际上它是一个更严格的限制[37]。关于这个问题的讨论远未结束。需要强调的是，真实的、人造的和自然的计算机大多在远离热力学平衡的条件下运行，因此由经典平衡热力学得出的兰道尔极限可能会被突破[38]。现在，让我们简要列出仍然存在的问题：
（i）兰道尔原理在热力学结构中的准确位置需要进一步明确。
（ii）兰道尔原理的相对论扩展仍然是一个未解决的问题，温度的相对论变换的精确推导和基础问题也尚未解决。
（iii）在开发最优计算协议（包括非图灵计算设备）以实现最小能量耗散的过程中，应用兰道尔原理非常重要[39]。
参考文献
参考文献可上下滑动查看
非平衡统计物理读书会启动！
集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元，以及多位国内外知名学者共同发起「非平衡统计物理」读书会。本读书会旨在探讨统计物理学的最新理论突破，统计物理在复杂系统和生命科学中的应用，以及与机器学习等前沿领域的交叉研究。
为什么神经网络能够学习？为什么生命系统能够实现自组织和进化？信息如何成为生命过程的重要组成部分？信息和能量之间有怎样的深刻关系？从宏观进入微观，热力学定律仍然保持不变吗？从相变预测到量子多体系统模拟，机器学习如何改变统计物理研究？从神经网络的能量景观到深度学习中的相变现象，统计物理学为理解和改进机器学习算法提供怎样的启发？「非平衡统计物理」读书会将带领大家一起探索这些有趣而深刻的问题。
详情请见：从热力学、生命到人工智能的统计物理之路：非平衡统计物理读书会启动！
6. 加入集智，玩转复杂，共创斑图！集智俱乐部线下志愿者招募
内容中包含的图片若涉及版权问题，请及时与我们联系删除
评论
沙发等你来抢