如今，大语言模型（LLMs）已渗透到我们生活的方方面面，从智能助手到内容创作，无不展现出其强大的能力。而支撑这些模型不断进化的背后，隐藏着一个谜一般的重要规律——尺度定律（Scaling Laws）。这些定律告诉我们，模型的性能并非随机提升，而是随着规模的扩大呈现出惊人的可预测性。


这里的“规模”主要指三个关键因素：模型的非嵌入参数数量  、训练数据集大小  ，以及用于训练的计算量  。令人着迷的是，当我们在这几个维度上扩大规模时，模型在交叉熵损失（一种衡量模型预测准确度的指标）上的表现会按照精确的幂律关系稳步提升。这种趋势甚至可以跨越七个数量级以上。这意味着，只要投入更多、更大的资源，模型的性能就会按照可预测的曲线变好，仿佛遵循着某种宇宙的基本法则。而其他一些看似重要的架构细节，比如网络的深度或宽度，在很大范围内对最终性能的影响反而微乎其微。


尺度定律不仅揭示了性能与规模之间的定量关系（例如，损失 与参数数量的关系大致是，其中），还指导我们如何在有限的计算预算下进行最优资源分配。例如，OpenAI 的尺度定律指出，为了达到最优的计算效率，我们应该训练非常大的模型，但不需要将它们训练到完全收敛。更具体地说，随着计算预算的增加，最优的策略是将绝大部分计算资源投入到增加模型尺寸上，而数据集大小和训练步数 的增长则相对缓慢得多。大型模型在样本效率上也表现更佳，能用更少的数据点或训练步骤达到同样的性能水平。人们利用这样的定律，可以在小规模进行试验，找到最好的方案，然后再增大模型尺度，极大地节约了试错成本。


这些精确且跨越多个数量级的幂律关系，不禁让我们思考：为什么会这样？是否存在某种更深层次的原理在起作用？


或许，我们可以从物理学中的“相变”（phase transition）现象中寻找一丝灵感。


想象一下水加热变成水蒸气。这是一个典型的相变过程。在相变过程中，系统的一些宏观性质（如密度、流动性）会发生剧烈变化。相变可以分为一级相变（如水的沸腾，伴随能量吸收和性质的突变）和二级相变（变化是连续的，但性质的导数可能不连续）。加热一块磁铁，当温度超过某个阈值的时候，磁性会突然消失，这就是二级相变。


我们在这里更感兴趣的是二级相变，它允许系统存在于一个独特的中间状态——“临界点”（critical point）。临界点是一个神奇的地方。以描述磁性材料的“伊辛模型”（Ising model）为例。这个模型由一个点阵组成，每个点代表一个自旋，可以是向上（+1）或向下（-1）。


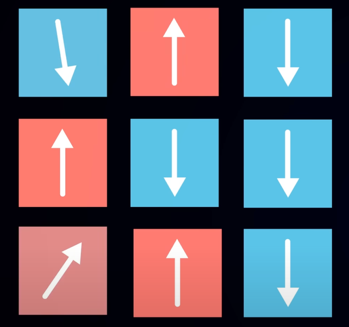
通过调整温度这个“控制参数”，我们可以观察系统的整体磁化强度这个“序参数”。在低温下，自旋倾向于对齐，系统呈现出宏观磁性；在高温下，热波动占据主导，自旋随机分布，磁性消失。有趣的是，在临界温度下，系统处于有序和无序的交界处。


在临界点附近，系统会展现出一些非凡的性质。最显著的是“长程关联”的出现。即使相隔很远，不同位置的自旋行为也会表现出关联性，这种关联性的空间范围——“关联长度”（correlation length）——在临界点处会发散。另一个重要性质是“尺度不变性”（scale invariance）或“自相似性”（self-similarity）。在临界点，无论你放大或缩小观察尺度，系统的统计性质看起来都是相似的，没有一个特征性的尺度。这种自相似性常常表现为各种性质遵循幂律关系。


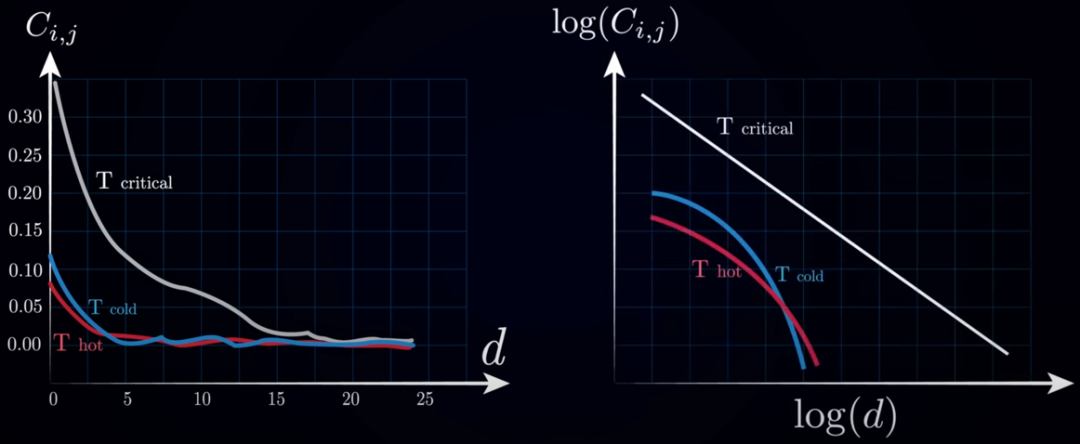
这种临界现象在自然界中普遍存在，甚至有大量证据表明，生物系统，特别是大脑，很多指标都遵循幂律关系，因而可能也工作在临界状态附近。研究发现，大脑神经元的活动会组织成不同大小的“神经元雪崩”（neuronal avalanches），这些雪崩的大小和持续时间惊人地遵循幂律分布。在一个简化的分支模型中，控制参数是“分支比率”（branching ratio），即一个激活神经元平均激活下游多少个神经元。分支比率小于1导致活动衰减、消失（亚临界），大于1导致活动爆发、达到癫痫发作（超临界），而等于1时活动既不衰减也不爆发，恰好处于临界状态。研究表明，在这种临界状态下，信息才能进行正常的传输。


引人遐想的是，大语言模型训练过程中的尺度定律所呈现的幂律关系，与临界系统中的标志性特征——幂律——有着惊人的相似性。这不禁让我们猜想：大语言模型的有效训练过程，是否也像物理系统或生物大脑一样，正是在某个抽象的“临界点”附近展开？


在这个猜想中，这个“临界点”可能不是物理上的温度或压力，而是模型规模（  ）、数据规模（  ）和计算量（  ）在某种复杂空间中的一个特定区域。达到这个区域，意味着系统（模型和训练过程）的各个组成部分和资源达到了某种微妙的平衡状态。就像大脑在临界点平衡兴奋和抑制以优化信息处理一样，大型语言模型可能需要在模型容量、数据多样性和计算投入之间找到一个最优的平衡点，才能以最高效率从数据中提取知识，并展现出泛化能力。而幂律行为，正是这种最优平衡状态（即“临界状态”）在宏观性能上的体现。


当然，这仅仅是一个基于现象的猜想或一种理解方式，目前我们还没有一个坚实的理论框架来完全理解这些尺度定律为何出现。临界性理论能否提供这样一个框架，将这些经验观察提升到更普遍、更具预测性的层面，还有待深入研究。可能需要发展一套适用于机器学习系统的“统计力学”理论，来解释为何这些宏观的、可预测的性能定律会从模型微观的参数交互和训练动力学中涌现。


但无论如何，这种跨领域的相似性本身就充满了魅力，不是吗？


参考文献：

[1] Jared Kaplan et al. Scaling Laws for Neural Language Models. https://arxiv.org/abs/2001.08361

[2] Artem Kirsanov. Brain Criticality - Optimizing Neural Computations. https://www.youtube.com/watch?v=vwLb3XlPCB4


图 | 朱成轩

文 | 李翰禹


—   版权声明  —

本微信公众号所有内容，由北京大学前沿计算研究中心微信自身创作、收集的文字、图片和音视频资料，版权属北京大学前沿计算研究中心微信所有；从公开渠道收集、整理及授权转载的文字、图片和音视频资料，版权属原作者。本公众号内容原作者如不愿意在本号刊登内容，请及时通知本号，予以删除。

内容中包含的图片若涉及版权问题，请及时与我们联系删除