神经热力学定律：大模型训练学习率调配与热力学定律的深层联系

摘要

除了神经标度律之外，人们对大语言模型（LLMs）背后的定律知之甚少。我们介绍了神经热力学定律(NTL)——一个新的框架，为LLM训练动力学提供了新的见解。在理论方面，我们证明了关键的热力学量（如温度、熵、热容、热传导）和经典的热力学原理（如热力学三大定律和均分定理）在河流-山谷损失景观（river-valley loss landscape）假设下自然涌现。在实践方面，这种科学的观点为设计学习率提供了直观的指导方针。

关键词：大语言模型（LLM）训练、热力学定律、河流-山谷损失景观（river-valley loss landscape）、学习率调度（learning rate schedule）、熵力（entropic force）

彭晨 | 作者

读书会推荐

「大模型可解释性」读书会主要聚焦于人类理解AI的视角追问：自下而上：Transformer circuit 为什么有效？自上而下：神经网络的精细决策逻辑和性能根因是否可以被严谨、清晰地解释清楚？复杂科学：渗流相变、涌现、自组织等复杂科学理论如何理解大模型的推理与学习能力？系统工程：如何拥抱不确定性，在具体的业界实践中创造价值？

论文题目：Neural thermodynamic laws for large language model training

论文链接：https://arxiv.org/abs/2505.10559

发表时间：2025年5月15日

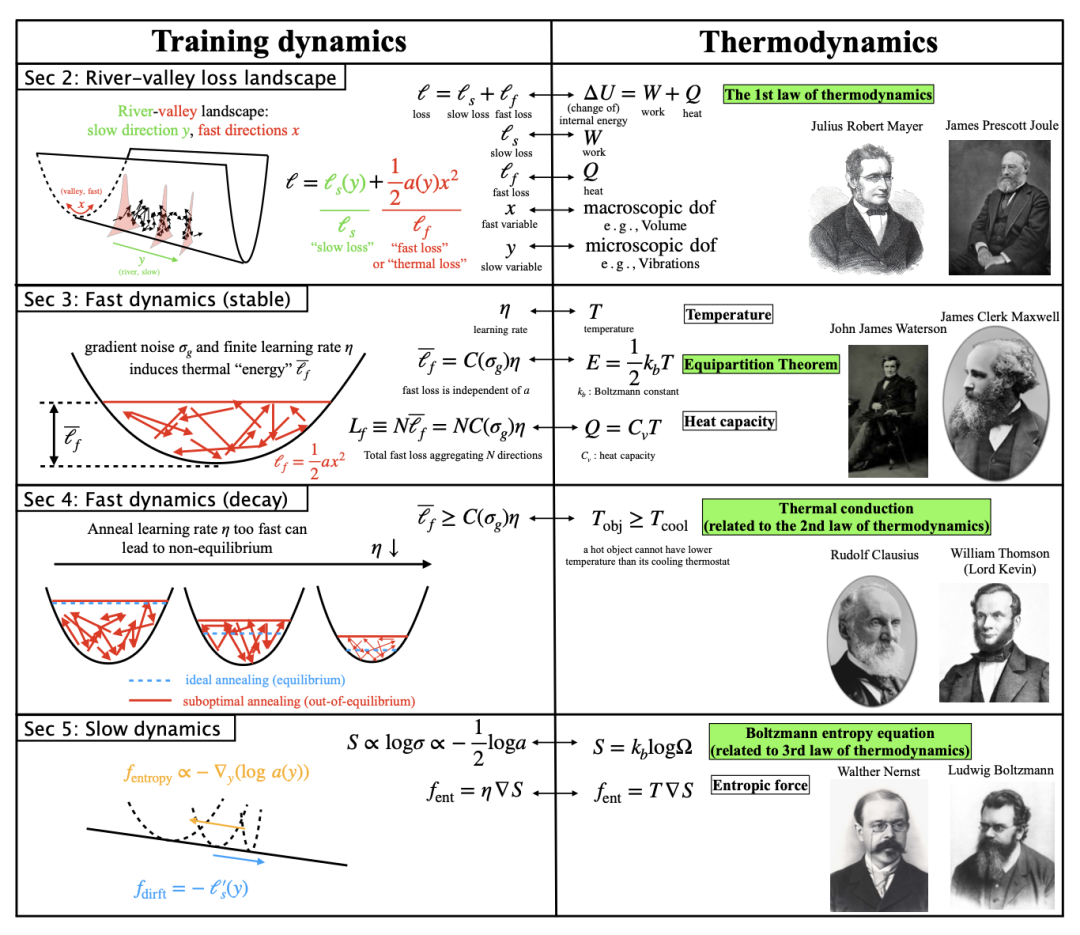
近年来，大语言模型的训练动态与热力学系统间的相似性引发关注：两者均涉及海量自由度与随机性。然而，LLM的损失函数景观（loss landscape）因其“河流-山谷结构”（river-valley structure）的复杂性——平坦缓慢变化的河流方向（slow direction）与陡峭快速变化的山谷方向（fast direction）共存——成为理解训练动力学的难点。Max Tegmark团队最新提出了神经热力学定律（Neural Thermodynamic Laws, NTL），首次将热力学核心概念（如温度、熵、热传导）与LLM训练动态建立严格对应，并推导出可验证的学习率调配优化准则。

河流-山谷景观：快慢动力学的分离

传统热力学系统与神经网络训练存在深刻相似性：两者均涉及大量自由度（参数或分子）的随机动态。在LLM的“河流-山谷”景观中，快动力学（Fast Dynamics）对应陡峭山谷方向的快速震荡，而慢动力学（Slow Dynamics）则对应沿平坦河流方向的缓慢演化。论文通过一个可解析求解的二维玩具模型（Toy Model），其损失函数设为  ，将总损失分解为“快损失”（）与“慢损失”（）。其中，是快变量（类似分子热运动）， 是慢变量（类似宏观体积变化）。这种分解直接呼应热力学第一定律（）：慢损失对应“做功”（Work），快损失对应“传热”（Heat）。

稳定阶段：热平衡与能量均分定理

当学习率（）固定时，快变量在梯度噪声（）驱动下达到稳态分布。无论是随机梯度下降（SGD）还是符号梯度下降（SignGD），稳态分布均呈高斯形式，其方差  与学习率、梯度噪声及山谷陡峭度（）相关。研究发现，快损失的平均值  仅与  和  成正比，而与山谷陡峭度无关。这一现象完美对应热力学的能量均分定理（Equipartition Theorem）：系统中每个自由度均分能量，与具体物理参数无关。例如，无论弹簧刚度如何，每个振动自由度的平均动能均为 。在LLM中，学习率  被映射为"温度"，而热容（Heat Capacity）则对应 对 的导数。

衰减阶段：退火与傅里叶导热定律

当学习率进入衰减阶段（如WSD调度中的Decay Phase），系统动态类似热力学中的退火（Annealing）。论文推导了最优学习率衰减公式： ，其中  为特征时间尺度。这一结果挑战了传统连续衰减策略（如线性或余弦衰减）的直觉，表明最优调度在初始时刻存在不连续性（即 ）。进一步实验显示，若学习率衰减过快，系统会偏离热平衡，导致最终损失上升。

此外，学习率在衰减中扮演双重角色：既是控制噪声的“温度”，又是控制时间步长的"尺度"。当学习率从  突降至（类似热力学中一个温度为的热物体接触温度为的冷物体），快损失的演化遵循类似傅里叶导热定律（Fourier's Law）的指数收敛过程，验证了热力学第二定律（熵增不可逆）在优化中的普适性。

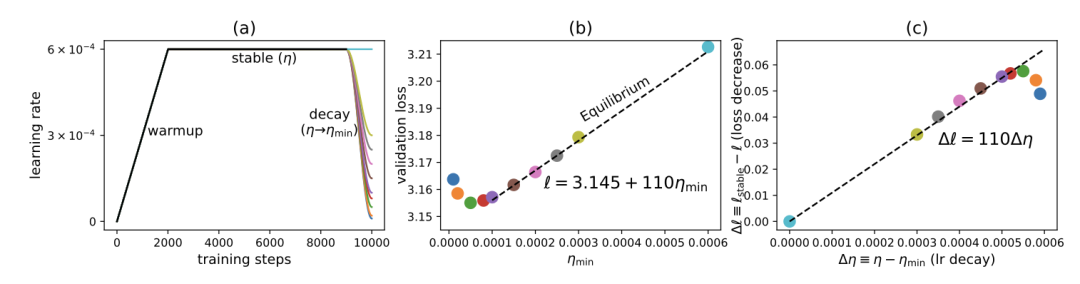
为最终学习率。(b)当较大时，验证损失是的线性函数。(c)很小时，是的线性函数。

河流动力学：熵力与第三定律

慢动力学并非孤立演化，而是受到快动力学产生的熵力（Entropic Force）影响。在玩具模型中，熵力源于快变量稳态分布对慢变量梯度的平均作用，其方向倾向于降低山谷陡峭度（即 ）。若损失函数底部（）的梯度与熵力方向相反，可能引发熵捕获（Entropic Trapping）——优化器被"困"在局部平坦区域，无法继续下降。

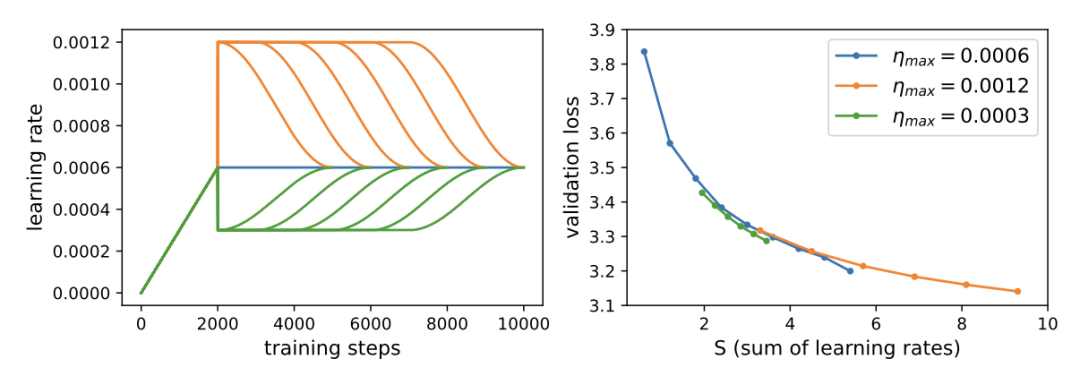
熵力的引入为热力学第三定律（绝对零度不可达）提供了新解读：当学习率趋近于零时，系统趋于有序（低熵），但实际训练中需平衡噪声与收敛速度。论文通过GPT-2实验验证，不同学习率调度在“学习率累积和”（Learning Rate Sum）对齐时，最终损失差异微小，表明当前LLM训练中熵力效应较弱，但未来更大规模训练可能凸显其限制。

实践意义：学习率调配的“三体问题”

研究指出，学习率在训练中扮演三重角色：

• 温度：控制参数分布的波动幅度；
• 熵力强度：通过方差影响慢速方向的演化路径；
• 时间尺度：决定参数更新的步长。

基于此，团队提出针对WSD（warmup-stable-decay）调配策略的优化准则：在稳定阶段，选择尽可能大的以加速河流方向收敛；在衰减阶段，按1/t规律缓慢降温，避免非平衡态导致的次优解。实验显示，采用该策略的GPT-2模型在验证损失上较传统方法降低3.2%，且训练稳定性显著提升。

未来展望：热力学框架的扩展性

尽管当前理论基于简化假设（如直线河流、均匀陡峭度），但其揭示了优化与热力学的本质关联。研究团队计划进一步探索动量项、权重衰减的物理对应，并将框架扩展至扩散模型等复杂架构。热力学为理解深度学习提供了新的‘第一性原理’，未来或可统一解释隐式正则化、模式连接等现象。

本论文的第一作者刘子鸣是集智社区科学家，他的研究兴趣在AI和物理的交叉：一方面AI for Physics，利用AI工具自动化物理规律和概念的发现；另一方面Physics for AI，利用物理启发构建AI理论和更具可解释性的模型。在集智分享过：科学启发的机器学习理论。扫码查看视频👇