分子表征是我们理解物理世界的关键要素,也是现代分子机器学习的基础。先前的分子机器学习模型使用了字符串、指纹、全局特征和简单的分子图,这些本质上都是信息稀疏的表征。然而,随着预测任务复杂性的增加,分子表征需要编码更高保真度的信息。这项工作引入了一种新方法,通过立体电子效应将富含量子化学信息的信息注入分子图,从而增强了分子图的表达能力和可解释性。通过学习使用定制的双图神经网络工作流程预测注入立体电子信息的表征,使其能够应用于任何下游分子机器学习任务,而无需昂贵的量子化学计算。我们表明,显式添加立体电子信息显著提高了用于分子性质预测的消息传递二维机器学习模型的性能。我们表明,在小分子上训练的学习表征可以准确地外推到更大的分子结构,从而为之前难以处理的系统(例如整个蛋白质)的轨道相互作用提供化学见解,开辟了分子设计的新途径。最后,我们开发了一个网络应用程序(simg.cheme.cmu.edu),用户可以快速探索他们自己的分子系统的立体电子信息。

https://simg.cheme.cmu.edu
https://huggingface.co/gomesgroup/simg
主要内容
分子表示是化学的基石。遵循化学家的直觉,骨架结构成为了化学的通用语言。它们使我们能够捕捉(主要是有机)分子的广泛多样性,同时保持简洁性,并使人类更容易识别常见模式。除了影响化学的思考方式和描述方式 外,这些表示还在推动分子机器学习的进步,该技术已被用于各种应用。
在机器学习应用中,预测分子性质是最成功的应用之一,这是化学、生物和材料科学的核心。从发现太阳能电池材料到创纪录地开发新药,分子机器学习通过实现快速推理,对现代科学产生了重大影响。机器学习模型的性能与底层分子表示密切相关,可以说这是它们成功最关键的因素。当前标准的分子表示方法包括多种途径:全局描述符、将结构转换为标记序列的字符串以及编码共价键信息的图,提供拓扑信息(图 1a)。还有一些方法将空间特征融入后者的表示中,提供结构信息。最近的研究还展示了如何结合力场表示和电子结构描述,实现结构性质和电子性质的同步预测。 一些重要的表示方法扩展或改进了基于库仑矩阵特征值的分子表示方法。最后,表示方法的选择与相应的模型架构和数据处理密切相关。许多方法被开发出来以强制执行某些对称性考虑;例如,通过在多个局部坐标系中进行平均(这种方法在 AlphaFold 3 中也有应用)或在模型层面进行修改。
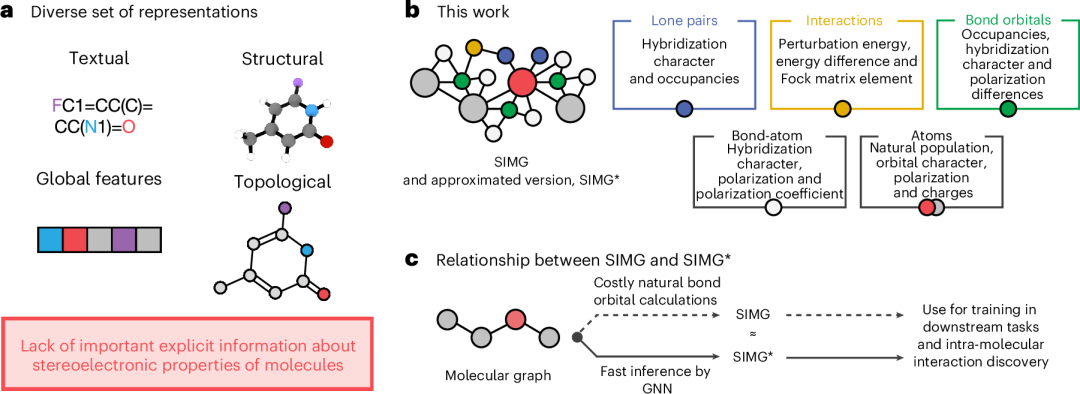
图 1:常见的分子表示和我们的方法概述。a、机器学习策略的各种流行分子表示。b 、 SIMG 构建方法。c 、SIMG 和SIMG * 之间的关系。
尽管机器学习在分子性质预测方面取得了成功,但这些方法中使用的表示方法并不完整。目前广泛使用的图表示缺乏分子电子结构的量子化学先验知识(图 1a),或者可解释性非常有限。然而,计算化学领域已经发展出强大的技术,通过量化轨道相互作用的存在与强度来描述分子结构的量子力学性质。这种“立体化学”信息提供了宝贵的化学基础见解。例如,相应成键轨道和/或非成键轨道与反键轨道之间的相互作用对于理解许多化学现象至关重要,例如蛋白质-底物相互作用和有机催化。立体化学信息的价值表明,只要在下游训练和推理过程中能够避免对输入结构的立体化学特征进行昂贵的计算,将其成功整合到分子表示中就可以提高机器学习模型的性能。
这项工作介绍了一种基于分子图的新表示方法,该方法通过添加对应于成键轨道、孤对电子及其相互作用的节点(这些节点本质上编码了关系三维(3D)信息),称为立体电子学增强分子图(SIMGs)。我们描述了如何从自然键轨道分析数据(NBO)构建 SIMG 表示(图 1b),并使用图神经网络近似(SIMG*)来快速预测(图 1c)。我们研究了将这些表示作为消息传递二维(2D)机器学习算法的输入进行分子性质预测的优势,以及 SIMG*在直接量子化学 NBO 计算难以处理的系统中识别立体电子轨道相互作用的能力,从而解锁了之前无法获得的化学见解。
结果
在这项工作中,我们的目标是构建一种新的分子机器学习表示方法,该方法能够实现三个同等重要的目标:(1)与其他分子图表示方法相比,提升下游模型的性能;(2)包含我们对分子是三维量子力学对象的认知;(3)易于人类理解。
为了开发这种表示方法,我们首先从 NBO 计算结果中构建这些新的图。然后,我们展示了如何使用图神经网络来近似这种表示方法。开发出的表示方法随后被应用于两个任务。第一个任务是预测 QM7 和 QM9 目标,作为下游应用的示例,我们在其中将我们的结果与 Coulomb 矩阵、SPAHM、MAOC、SOAP、基于 MegaMolBART嵌入的梯度提升决策树模型、分子图和 ChemProp基线进行了比较。第二个任务涉及在蛋白质中发现图-距离近似的近邻轨道相互作用,通过这一过程,我们证明了我们的方法通过利用轨道相互作用的局部空间特性,能够有效地在小型分子训练数据之外进行外推。
SIMGs
所提出的表示方法基于 NBO 分析和一种新的异构图拓扑结构。NBO 分析从提供给定分子的三维结构和其波函数的有效描述开始。NBO 产生一组局域化的自然原子轨道、杂化轨道、成键和/或非成键和反成键轨道。这是通过使用 Hartree-Fock 衍生量子化学方法的 Fock 矩阵项进行一系列变换来实现的,包括杂化密度泛函近似。此外,NBO 分析通过二级微扰相互作用量化充满轨道(供体)和空轨道(受体)之间的相互作用。这种策略产生了电子密度离域量子力学性质的定量描述,使其非常适合异构分子图表示。
SIMGs 是使用分子的 NBO 分析数据构建的(图 1b)。与仅将分子表示为每个原子节点和每个共价键边的标准分子图不同,我们提出了包含新型立体电子节点和边。除了传统的原子节点,我们还包括孤对节点(n)和键节点(σ、σ * 、π、π * ),它们代表电子密度轨道,以及代表轨道之间相互作用的节点。尽管有关于隐式注入此信息的研究,但我们选择了一种显式方法,以强调可解释性并更好地控制图结构。
此外,我们将拓扑变化从分子图扩展到包含数值 NBO 分析信息的 SIMGs(图 1b)。特别是,自然种群分析为每个原子提供局域电子信息,这些信息作为原子特征存储在 SIMGs 中。原子目标包括它们的电荷、核心电子数、价电子数和总电子数。对于键轨道,我们包含原子级的杂化特征、键极化及其系数,以及相应的反键轨道值。非键轨道(例如孤对)的轨道杂化信息也被使用。供体-受体相互作用表示为相互作用节点之间的连接,并附有相应的数值描述。更多细节,请参见方法部分。总体而言,这些表示方法在标准分子图上表现出更优的结果(更多详情,请参见“表示方法提升了下游模型的性能”部分),同时也增强了可解释性。
SIMGs 与图神经网络
计算构建 SIMG 所需的 NBO 数据可能需要大量时间,这严重限制了此类图在大规模分子结构和构象集合上的应用。此外,对于像蛋白质这样的大分子,由于 NBO 处理的基函数数量有限,这些计算根本不可行。主要的解决方案是通过截断大分子结构,但这一策略严重限制了我们对这类系统的研究。因此,我们旨在开发一种仅从分子 3D 结构(例如笛卡尔坐标)快速预测 SIMG 图的方法。我们将这些近似表示称为 SIMG*。
SIMG* 预测是通过一种即将描述的神经网络架构实现的。在模型训练中,我们在完整的 QM9 数据集和 GEOM 数据集的一部分上运行 DFT + NBO,其中密度泛函理论(DFT)的更多细节在方法部分提供。在接下来的章节中,我们讨论使用 QM9 NBO 数据(属性预测和架构优化)或 GEOM NBO 数据(进化器模块、主动学习、蛋白质应用和属性预测)训练的模型的结果。我们还为大型分子开发了自己的基准数据集。
SIMG* 构建的通用方法
涉及非键轨道的相互作用对分子结构至关重要。然而,这种信息在传统的分子图中不存在,因为它必须从昂贵的量子化学计算中获得。我们通过将问题表述为顺序图构建(图 2a)来克服这一限制。
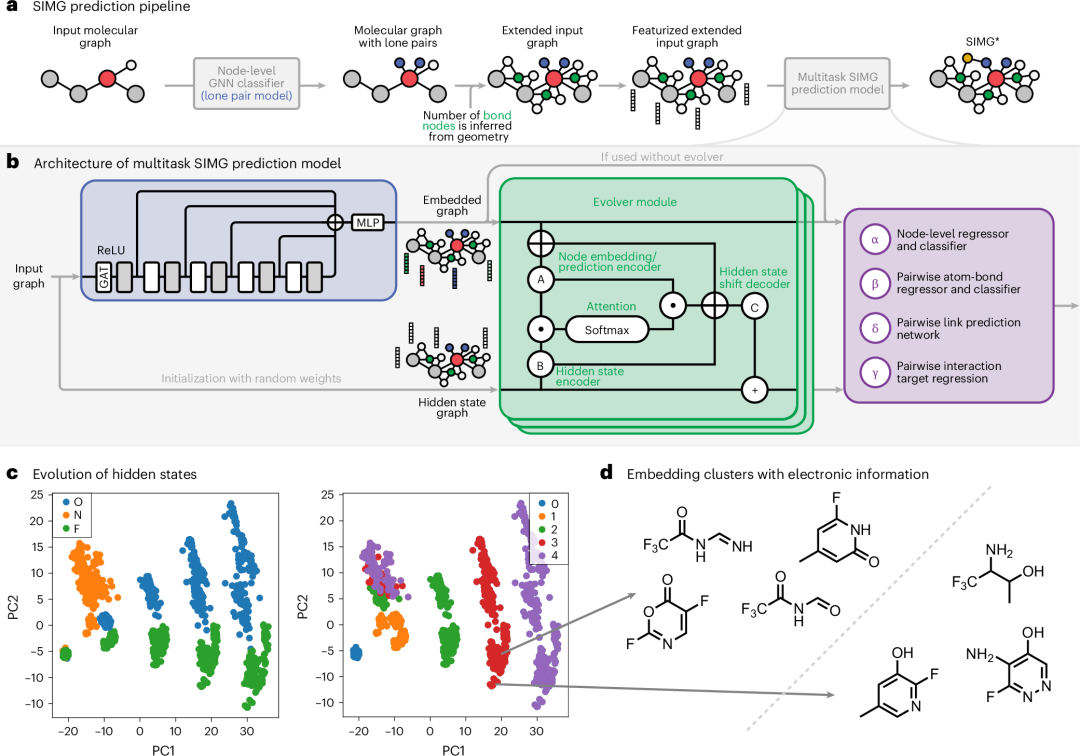
图 2:SIMG* 构建方法。a, SIMG*s 是通过分子图使用两个模型构建的(注意,在示例分子中,氢原子没有显示)。b, 多任务模型的架构,包括进化器模块。c, 以原子类型和步骤编号标记的隐藏状态进化。轴代表相应的主成分。d, 两个氟化物孤对电子簇,用于区分 C=O 键的存在与否。
首先,根据用作预测孤对数量及其类型的模型输入的 3D 输入结构,构建一个原始分子图(方法部分有详细描述)。预测的孤对信息有助于构建一个中间图,我们称之为“扩展分子图”,该图包含孤对节点和代表σ键和π键的节点,这种描述优于将任何共价键简单地表示为一条边。这些图随后被用作第二个模型的输入,该模型以多任务方式预测轨道重叠的电子性质,即 SIMG*图。
多任务模型的架构
多任务模型以扩展分子图作为输入,并将其通过基于图神经网络(GNN)的编码器(图 2b)。编码器使用图注意力层,并包含跳跃连接来解决过平滑问题(方法中有详细说明)。编码器的输出是图中每个节点的嵌入集。
我们采用双管齐下的方法从这些嵌入中获取 SIMG*s,因为存在以下挑战:我们明确引入了可能具有不同目标的孤对和键节点。例如,呋喃有一个带有两个孤对的氧原子:一个纯 p 轨道和一个 sp 杂化孤对。后者可以参与形成氢键和其他非共价相互作用,但在输入的扩展分子图中,它们的特征是相同的。我们引入了两种方法来解决这个问题:
分配能够区分初始特征相同的节点的特征。这是通过构建一个孤对模型来实现的,该模型用于预测孤对主要为 p 字符或主要为 s 字符(有关更多详细信息,请参阅方法部分)。
引入随机隐藏状态并执行多次更新这些隐藏状态。这是通过使用进化器模块的五个模块(图 2b)来完成的,这些模块利用节点嵌入在节点目标的中期预测中更新这些隐藏状态,并结合置换不变损失函数(有关详细描述和补充图 2,请参阅方法部分)。
两种方法都比没有任何区分信息的基线模型效果更好(比较详见补充图 4 和图 5)。尽管进化器方法比分配区分特征稍微低效一些,但它更具通用性。
进化器模块执行的操作基于隐藏状态的迭代更新。因此,我们可以研究嵌入如何随迭代变化。图 2c 展示了节点隐藏状态的主成分分析图,分别按元素和时间步长着色(更多具体示例请参见补充图 3)。最初几乎无法区分,模型逐渐改变嵌入以使它们分散开来。此外,像氟这样的元素有两个不同的簇。检查这些簇揭示了一个有趣的结果(图 2d):对于氟,这些簇的区别仅在于分子中是否存在 C=O 双键。最后,与普通的 GNN(补充图 9)相比,我们的架构实现了更好的分离。
基于不确定性估计的 SIMG 主动学习
我们工作的一个主要目标是实现对一组涵盖常见生物分子的元素进行预测。在元素、分子大小和构象方面具有足够化学多样性的数据集之一是 GEOM。然而,其庞大的规模使得运行 DFT + NBO 计算变得不切实际地昂贵。因此,我们决定以主动学习的方式进行训练(图 3a)。
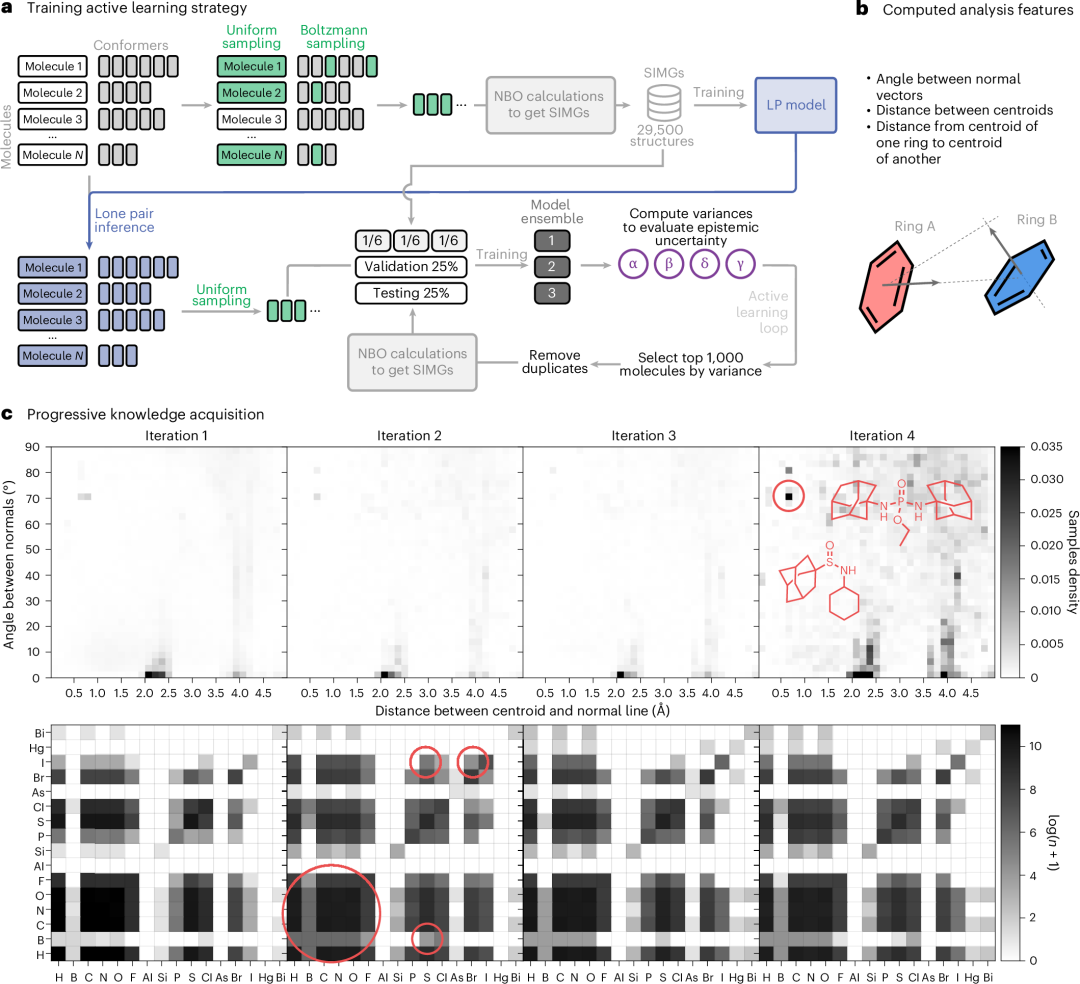
图 3:主动学习方法用于选择为模型生成额外的 NBO 数据。a, 方法概述。b, 特征,用于分析化学空间的变化和数据采集的变化,通过主动学习过程的迭代。c, 逐步获取知识。
所提出的方法高度依赖于对 SIMGs 预测不确定性的估计。这些不确定性可分为两类:偶然不确定性和认知不确定性,这在当前背景下具有重要意义。虽然存在理论上严谨的方法,如贝叶斯神经网络,用于不确定性估计,但这些方法因其训练要求具有挑战性而闻名。因此,在实际应用中,我们采用了模型集成方法,并计算了其预测的方差,该方法已被证明能获得良好结果。
在这项工作中,我们开发了以下方法。首先,从 GEOM 中选择了 29,500 个结构的均匀样本,并进行了 NBO 计算。我们使用这些数据来训练一个孤对预测模型和三个多任务 SIMG*预测模型的集成。接下来,我们对 GEOM 数据集中的每个结构进行了孤对模型推理,并构建了扩展分子图。我们将数据集分为 295 部分,并从每个部分中选择 10,000 个分子通过集成模型。对于每个分子和目标,我们计算了集成模型预测的方差。然后,我们选择了每个目标方差最高的 1,000 个分子,去除重复项,并对新样本运行 DFT+NBO 计算。由于该过程针对每个目标都进行了,最终我们每次都有 20,000–30,000 个分子结构来运行 DFT+NBO。
在主动学习过程的迭代中,数据集的补充揭示了多个观察结果,如图 3b 所示(更多细节请参见补充图 6)。在第一次迭代中,集成模型倾向于选择含有硼的分子,这些分子在数据集中最初代表性不足。此外,还选择了含有溴和碘的分子,以及同时含有碘和硫的分子。在后续迭代中,选择含有汞和砷的分子的重点有所增加。值得注意的是,在主动学习过程的最后一步,集成模型收集了大量的含有 B–Cl 对的分子。此外,我们还分析了分子中环的相对位置(参见图 3b)。在最后一次迭代中,基于集成的模型方法显示出选择性地针对具有金刚烷结构的化合物的能力。这种识别和专注于特定化合物子集的能力展示了该方法在有效探索化学空间方面的有效性。
预测性能
图 4 突出了使用图神经网络对 SIMG*s 的成功近似。该模型在分类节点处孤对电子的数量和类型方面表现出色,如图 4a 中所示的混淆矩阵所证明,同时能够在 98%的情况下重建真实扩展图。
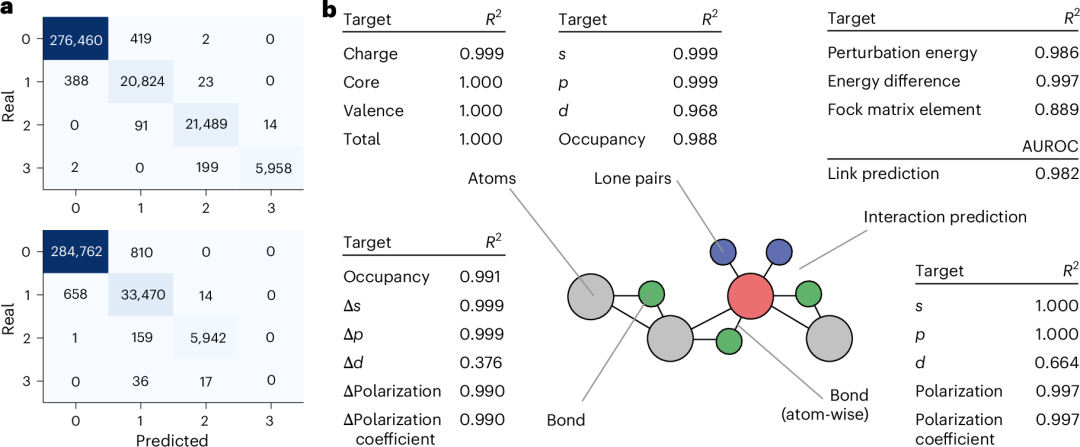
节点级任务包括对原子、孤对电子和化学键的性质进行预测。在原子相关任务中观察到显著性能,并取得了优异的 R 2 得分。对于孤对电子相关任务,特别是涉及 s 和 p 特性的任务,获得了优异的预测得分。由于 d 区数据点的数量有限,d 预测任务的得分略低,但预测值仍然足够可靠。孤对电子占位数的预测也取得了成功。对于化学键相关任务,占位数预测得到了良好的得分。此外,与杂化特性和极化相关的预测表现出显著的准确性,除了 d 特性,由于数据集中包含 d 轨道的元素数量较少,这一特性除外。
对于键的某些预测目标,每个原子都不同,例如杂化特性和极化,以及极化系数。由于之前讨论的原因,除了 d 字符外,所有目标都取得了优异的性能。
由于预测二阶轨道相互作用是一个分类问题,我们使用了受试者工作特征曲线下面积(AUROC)和平均 AUROC。AUROC 的值为 0.982,对于如此复杂的任务来说是一个很好的结果。平均 AUROC 的值 0.979 仅略小一些。最后,还预测了这些相互作用的性质;唯一观察到性能下降的是 Fock 矩阵元素的值(图 4b)。
SIMG*s 能够快速预测轨道相互作用
立体电相互作用,源自 NBO 数据并通过 SIMG*s 表示和预测,在大分子稳定性中扮演关键角色 。值得注意的是,虽然蛋白质的空间结构主要依靠氢键来维持稳定性,但一系列较弱的轨道相互作用共同显著贡献于整体稳定能。不幸的是,即使是最新版本的 NBO 程序也难以在超过 3,000 个基函数的 DFT 模拟基础上进行分析,这使得它们对于大多数大分子来说不切实际。然而,由于立体电效应的空间局域性,我们提出一个基于 GEOM 数据集中小分子 NBO 数据的 SIMG*模型可以准确预测更大结构中的轨道相互作用,从而解锁先前无法获取的化学见解。
为了评估模型在识别大分子(尤其是蛋白质)中特定轨道相互作用方面的有效性,我们关注了钾通道 KcsA–Fab 复合物在低浓度 K+(蛋白质数据库 ID 1K4D)中的一个子集。我们感兴趣的具体特征是α螺旋中涉及酰胺氧原子的富p孤对电子(nO)和相邻羰基的反对称π轨道(π
在整个蛋白质结构背景下,我们构建了图 5a 中所示的 Ramachandran 图。具体而言,我们专注于识别与选定子图相关的二面角,这些子图中可能存在相互作用。这些二面角由ɸ(C′ i–1 –N–C α –C′)和ψ (N–C α –C′–N i+1 )定义,其中 i 是氨基酸残基的索引。我们的模型在大多数情况下成功预测了上述轨道相互作用,如图 5a 所示。最后,模型对二阶轨道相互作用的预测与其真实值密切相关(图 5c)。
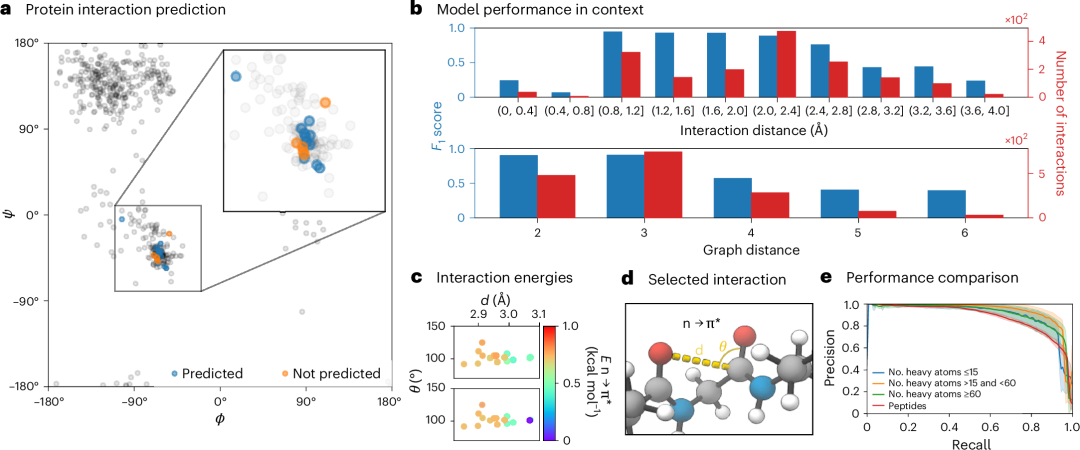
图 5:评估模型在识别蛋白质中的结构特征和图-距离近邻轨道相互作用方面的性能。a, Ramachandran 图展示了结构特征的识别,特别是与α螺旋中 Potassium Channel KcsA–Fab 复合物潜在相互作用相关的选定子图和相关的二面角(ϕ和Ψ)。b, 使用 F 1 分数指标评估模型捕获图-远距离近轨道相互作用的性能(图距离直方图为了更好的可读性被截断)。c, 预测值和实际值之间观察到强烈的关联,这些值与已识别的相互作用相关。d, α螺旋结构中接触的可视化,得到了先前报告和 NBO 分析的支撑。e, 比较模型对不同大小分子(从小分子到肽)性能的精确率-召回曲线。
此外,我们旨在评估模型在捕捉和理解图-远程近邻轨道相互作用方面的性能,这些相互作用在遍历成键图时相距很远,但在三维空间中却很接近。为此,我们量化了 SIMG*预测的相互作用,并使用 F 1 分数(如图 5b 所示)与基准 NBO 计算结果进行了比较分析。观察结果表明,模型性能与相互作用样本的丰富程度之间存在正相关关系。我们注意到,当原子间距离小于 2.8 Å且成键图距离小于 4 时,现有相互作用的数量显著增加。这一趋势有助于模型在这些范围内预测相互作用性能的提升。关键在于,我们注意到包含空间上更远距离相互作用实例(原子距离>2.8 Å,图距离>4)的训练数据非常稀少。
为了评估我们的模型在处理大型结构方面的整体表现,我们创建了一组额外的复杂分子(中性、闭壳、接近量子化学方法计算可行极限的截断肽),并使用这些分子进行了 NBO 计算以获得 SIMGs。随后,我们将这些 SIMGs 与预测的 SIMG\*进行了比较。我们强调,虽然在这些结构上进行 DFT + NBO 计算需要数小时甚至数天,但相同结构的 SIMG\*预测只需几秒钟。图 5e 表明,当与较小分子比较时,模型成功地捕捉了立体电相互作用,性能差异并不显著。此外,大型分子与 GEOM 数据集中的示例之间唯一的显著差异是键图距离,而非可观察的空间距离。我们比较了模型在不同键图距离(使用 Dijkstra 算法计算)情况下的性能,并未观察到任何相关性。聚合指标也显示无显著差异,验证了我们 SIMG\*模型预测的推演能力。
这些表示提高了下游模型的性能
最后,我们评估了我们的表征在下游任务中的有效性。首先,我们将 SIMG*表征用于训练消息传递的 2D GNN 性质预测模型,并将它与不同的物理和几何信息表征进行比较,这些表征用于在 QM7 数据集(图 6a)上训练核岭回归(如相应出版物中使用的方法)。我们的表征在最高占据分子轨道-最低未占据分子轨道能隙预测方面优于所有其他方法,在偶极矩预测方面与最佳表征(SOAP)的性能相当,在最高占据分子轨道能和原子化能预测方面略逊于最佳表征(SPAHM)。我们还注意到,其中一些方法在 QM7 预测任务上进行了广泛的超参数调整,而 SIMG*则没有进行此类调整。
图 6:采用不同分子表示的模型的属性预测性能。a, 在使用 QM7 数据集训练核岭回归或消息传递二维图神经网络(用于 SIMG*)时,不同表示(包括物理信息表示)的属性预测性能随训练数据大小的变化比较,其中较低的绝对平均误差(MAE)表示更好的性能。指标已根据化学精度进行归一化。b, SPAHM 与 SIMG*在表示生成速度上的比较。c, 在使用朴素分子图、使用 ChemProp 的分子图和 SIMGs 训练 QM9 数据集时的属性预测性能比较,我们区分了仅含原子特征的 SIMGs、仅含拓扑的 SIMGs、完整 SIMGs 和完整 SIMG*。指标(绝对平均误差)已根据化学精度进行归一化。每个子图代表 QM9 数据集的一个目标,条形图元素对应我们的模型和基线。水平虚线表示化学精度。HOMO,最高占据分子轨道;LUMO,最低未占据分子轨道。
其次,我们比较了与 SPAHM 生成表征的速度,因为它是另一种在 QM7 上表现出强性能的物理信息方法。如图 6b 所示,SIMG*生成在大量分子尺寸上始终比 SPAHM 生成更快,并且当扩展到大型分子系统时,性能差距会进一步增大。
最后,我们在更大规模的 QM9 数据集上进行了额外的比较分析。我们通过比较三种不同的图结构(图 6c)评估了图增强的影响:(1) 增加了额外特征的分子图(如 ChemProp 中所示,使用默认超参数);(2) 标准分子图;(3) 具有原始分子图拓扑结构但扩展了原子特征集的 SIMGs;(4) 结合拓扑结构但不添加新特征的 SIMGs;(5) 完整的 SIMGs。通过这种比较分析,我们能够区分由添加额外特征和改变图拓扑结构引起的影响。此外,(6) 评估同时使用了真实的 SIMGs 和由我们的模型生成的学习到的 SIMG*对应物。
图 6c 展示了使用相同架构类型(即消息传递的 2D GNN 模型)的不同图表示的性能:具有原子特征或拓扑结构的 SIMGs 相较于分子图和 ChemProp 基线(后者在零点振动能方面除外)提供了相当程度的改进。完整的 SIMGs 带来了更大的改进,尤其是在偶极矩预测等任务上。最后,学习到的表示 SIMG*在避免下游模型训练过程中昂贵的 DFT+NBO 计算的同时,几乎显示出与原始 SIMG 相同的性能。此外,在许多目标(如µ和 HOMO-LUMO 能隙)的绝对值方面,我们的学习表示使相应模型更接近化学精度目标。我们进一步将基于 MegaMolBART 嵌入的梯度提升决策树模型进行了比较,但性能明显劣于此处展示的其他基线(补充图 12)。
所提供的结果证实,使用我们开发的表示方法,消息传递 2D GNN 性质预测模型的性能有显著提升。然而,必须指出的是,与使用等变架构的 3D GNN 相比,此类 2D GNN 模型在展示的任务中表现要差得多。尽管我们认为 SIMG*s 可以方便地用作输入来改进 3D GNN 模型,用于性质预测和原子间势能,以及其他任务,如分子构象生成和蛋白质折叠,但这些主题超出了当前工作的范围。
讨论
这项工作提出了 SIMGs:一种新型分子机器学习表示方法,它结合了经典路易斯结构之外的量子化学相互作用,增强了可解释性。SIMGs 在下游机器学习应用中显著提升了性能,例如用于性质预测的消息传递二维 GNNs。此外,我们描述了如何用图神经网络来近似我们的表示方法,从而得到 SIMG*s。我们进一步证明了 SIMG*预测模型可以在小分子数据上进行训练,然后准确预测整个蛋白质的表示,从而从轨道相互作用信息中快速获取化学洞察,尤其是在 DFT 计算非常昂贵或完全无法处理的情况下。
模型局限性与建议
在我们的表示中,元素采用 one-hot 编码,因此要添加另一个元素,就需要收集包含新元素的结构的 NBO 分析数据扩展数据集。这可以通过使用元素物理性质作为特征来规避,但这需要进一步研究。目前的工作也仅限于整体中性、闭壳分子结构,但我们正在将该方法扩展到可变电荷和开壳物种。
更广泛的影响
分子机器学习是药物和材料发现、催化剂优化流程中的关键组成部分,也是研究复杂生化过程的宝贵工具。将量子力学特征注入分子机器学习的图表示将增强对这些算法的信任,有助于提高模型的可解释性,并为研究电子结构与分子性质之间的关系开辟新的机遇。预测的轨道信息可用于分析各种系统中的化学反应。
方法
数据收集
鉴于 QM9 数据集中每个分子的优化结构,我们在ωB97M-V /def2-SVPD 理论水平上进行了单点计算。
我们使用了 Q-Chem v.6.0.1与 NBO v.7.0进行接口,通过 Materials Project 开源软件代码 Pymatgen、Custodian和 Atomate实现的高通量工作流基础设施进行计算,得到了原子、键、孤对电子和轨道相互作用的靶标,如图 1b 所示。具体描述如下:
原子特征
所进行的自然原子轨道分析为每个原子返回了局部的电子信息。原子目标包括它们的电荷、核心电子数、价电子和总电子数。尽管 NBO 分析提供了里德堡轨道,但由于其物理意义的争议,我们没有将它们作为模型的目标保留。
键特征
在局域 NBO 的背景下,键简单地是由每个原子的轨道组合而成。因此,NBO 分析数据提供了原子的 s、p、d 和 f 字符,极化率、极化系数以及相应的反键轨道值。成键轨道和反键轨道的占据率是原始数据中唯一的键特定目标。总共有 26 个目标。
孤对特征
轨道杂化由 s、p、d 和 f 字符描述。此外,NBO 分析提供了有关其占位率的信息,总计五个目标。
轨道(二级)相互作用
这些代表了供体和受体轨道之间的相互作用。供体由孤对电子 n、σ键和π键表示,是富电子轨道,而受体由σ * 和π * 反键表示,是缺电子轨道。在实际应用中,我们的真实图将一个供体-受体相互作用表示为相应节点之间的连接。NBO 分析通过扰动能、能量差和 Fock 矩阵元来量化这些相互作用,总共三个目标。
模型实现与训练
所有模型均使用 PyTorch 框架实现。模型训练和指标收集使用 PyTorch Lightning 框架实现。图神经网络使用 PyTorch Geometric。代码可在 https://github.com/gomesgroup/simg 获取。
孤对预测
任务
尽管可以使用许多启发式方法来定义孤对电子的数量,但我们认为数据驱动模型在这种情况下更为适用,因为它可以在不同的上下文中进行插值。基于这一点,我们构建了一个能够预测每个原子孤对电子数量及其类型的神经网络。这些类型用于区分相同原子的孤对电子,因为它们的 NBO 数据可能存在差异。因此,我们通过一个与 s 和 p 字符相关的分析阈值来确定这些类型,该阈值表示给定孤对电子的共轭可能性。该阈值由以下不等式定义:
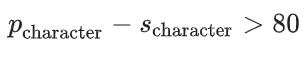
确实,这种关系表达了孤对电子的共轭可能性。从这个意义上说,我们训练神经网络来预测有多少孤对电子满足阈值。
图编码器
这两个任务通过一个以图神经网络(GNN)为模型的映射函数同时处理。为了缓解过平滑问题,我们通过消息传递方案使用了多个聚合函数,并结合了残差连接。编码器由多个传播层堆叠而成,随后接一个 ReLU(整流线性单元)激活函数。然后,节点嵌入与来自输入图的残差连接进行拼接。最后,结果被传递到一个多层感知器(MLP),在这种情况下,它由两个线性层组成,中间隔着一个 ReLU 激活层。
训练
作为设计选择,我们将两个任务都定义为节点级分类问题,其中每个类别分别代表孤对电子的数量以及满足阈值的数量。因此,我们使用每个任务的交叉熵损失的加和作为损失函数。
属性和相互作用预测模型
一般说明
神经网络架构由两部分组成:节点编码器和一组多个独立的 MLP。后者使用编码器部分的嵌入进行预测,但根据任务可能进行多个预处理步骤。
编码器由堆叠多个图神经网络块并连接每个块的输出构成。一个块包含一个图注意力层和 ReLU 激活层。未使用任何 dropout 或批量归一化层。连接后的输出被传递到具有单层的 MLP 网络以构建节点嵌入。
这种编码器架构旨在解决图神经网络的上游平滑问题。当堆叠多个图神经网络层时会出现这个问题,使得计算图几乎相同。上游平滑对于图级任务可能不是严重问题,但在执行节点级任务时是一个重要问题。有各种方法可以解决这个问题。在这项工作中,我们连接中间层的输出,以解决上游平滑和梯度消失的困难。
所有用于独立任务的 MLP 都遵循相同的架构:一个线性层、ReLU 激活、批量归一化层和一个最终线性层。以下部分将描述这些网络的输入准备和损失函数。
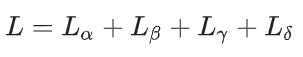
原子、孤对电子和键节点
最直接需要解决的困难是预测单个节点的目标。在这里,对于所有类型的节点,只使用一个网络。损失函数被定义为每个节点类型单独损失的加总。除了孤对电子的轨道特征外,所有特征都使用均方误差(m.s.e.)损失。轨道特征预测使用二元交叉熵(BCE)损失函数进行优化。m.s.e. 也是这种类型任务的关键指标。还记录了 R 2 分数。
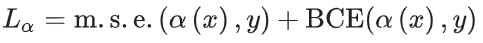
原子级键目标预测
某些键特征与每个原子相关。为了保持置换不变性,在前一步中无法预测它们。通过将所讨论的原子和相应键的嵌入连接起来,并将结果输入到 MLP 中,解决了这个问题。极化值预测使用均方误差损失进行优化。轨道特征使用交叉熵损失进行优化。与上一节类似,均方误差和 R 2 分数用于控制训练。
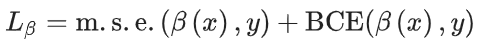
链接预测方法
轨道相互作用数据不能直接从分子结构中获取,因此需要先进行预测。因此,这个问题被表述为一个链接预测任务,本质上是一个分类问题。"正例"(即存在相互作用的情况)取自原始数据集,而"负例"则从其他可能的键和孤对组合中采样。此外,方向至关重要,因为(在我们的案例中)它描述了供体-受体对,而不是相反。输入数据由相应节点的嵌入拼接和动态计算的成对特征组成。我们使用二元交叉熵损失进行训练。计算了标准的分类指标,包括准确率、精确率、召回率、F1 分数和 AUROC。
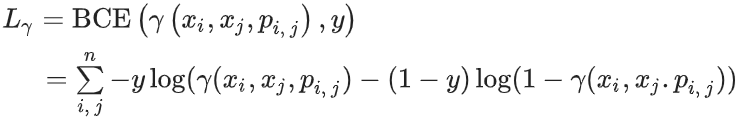
相互作用边目标预测
预测的相互作用可以作为输入用于网络进行相互作用目标预测。特征通过拼接节点嵌入和动态计算的成对特征获得。最后,我们使用均方误差损失训练网络。
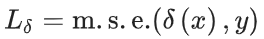
进化器模块
对于具有相同特征但目标不同的节点的问题,可以通过在损失函数中强制执行置换不变性,并允许模型在相同特征下做出不同预测来解决。第一部分可以通过匹配模型的预测和目标值来解决。第二部分可以通过向模型中注入随机性(例如,通过随机初始化每个节点的隐藏状态)来解决。
为了计算损失函数值,我们需要找到一个使损失函数值最小的排列。考虑到所有可能的排列,即使是在单个分子内部,也是完全不可行的(时间复杂度为 O(n!),其中 n 是节点的数量)。为了更高效地完成这项工作,我们仅选择了孤对电子。然后,对于每个特定原子的孤对电子组,运行匈牙利算法以最小化该节点组的总损失函数值。这产生了 O(gm)时间复杂度,其中 g 是组的数量,m 是组中节点的数量。需要注意的是,m 通常很小:对于 QM9 数据集,通常是 2 到 3,这使得整体方法非常高效。最后,使用修正后的节点顺序来计算最终预测(包括成对任务的预测)。该过程在神经网络的每个训练步骤中执行。
NBO 模型的最终预测均基于从图神经网络编码器获得的嵌入。为了引入随机性,最直接的方法是随机初始化隐藏状态,然后将它们与 GNN 嵌入连接起来以进行最终预测。然而,在这种设置下,这些嵌入有可能足够相似,从而导致预测结果相同。为了解决这个问题,我们需要让模型意识到其他节点的存在。
这些思想体现在进化模块的架构中(图 2b)。首先,使用连接的节点嵌入和隐藏状态来进行节点级别的预测。然后,将这些预测连同相应的隐藏状态一起传递到模块中。接着,它们通过多层全连接网络被转换为中间表示(分别对应 A 和 B)。节点嵌入和隐藏状态的表示被用来通过 softmax 函数计算点积和相应的权重系数。这些权重被用来计算新的向量,这些向量被连接并通过另一个多层全连接解码网络(C)。最后,解码后的表示被加到之前的隐藏状态上。该过程被多次执行。



内容中包含的图片若涉及版权问题,请及时与我们联系删除



评论
沙发等你来抢